Нахождение точек на линии с заданным расстоянием
У меня есть вопрос, я знаю линию, я просто знаю ее наклон (m) и точку на ней A (x, y) Как я могу вычислить точки (фактически две из них) на этой линии на расстоянии (d) от точки А??? Я спрашиваю это для нахождения интенсивности пикселей на линии, проходящей через A (x, y) с расстоянием. В этом случае расстояние будет количеством пикселей.
5 ответов
Я бы предложил преобразовать линию в параметрический формат вместо точки-наклона. То есть параметрическая функция для линии возвращает точки вдоль этой линии для значения некоторого параметра t. Вы можете представить линию в качестве контрольной точки и вектор, представляющий направление линии, проходящей через эту точку. Таким образом, вы просто перемещаетесь на d единиц вперед и назад от точки А, чтобы получить другие свои очки.
Поскольку ваша линия имеет наклон m, вектор направления равен <1, m>. Так как он перемещает m пикселей по y для каждого 1 пикселя по x. Вы хотите нормализовать этот вектор направления на единицу длины, поэтому вы делитесь на величину вектора.
величина = (1^2 + м ^2)^(1/2)
N = <1, м> / величина = <1 / величина, м / величина>Вектор нормализованного направления равен N. Теперь вы почти закончили. Вам просто нужно написать уравнение для вашей строки в параметризованном формате:
f (t) = A + t * N
Это использует векторную математику. В частности, скалярное умножение вектора (вашего параметра t и вектора N) и сложение вектора (A и t*N). Результатом функции f является точка вдоль линии. 2 точки, которые вы ищете, это f(d) и f(-d). Реализуйте это на языке по вашему выбору.
Преимущество использования этого метода, в отличие от всех других ответов, состоит в том, что вы можете легко расширить этот метод для поддержки линии с "бесконечным" наклоном. То есть вертикальная линия, такая как x = 3. Вам не нужен наклон, все, что вам нужно, это нормализованный вектор направления. Для вертикальной линии это <0, 1>. Вот почему графические операции часто используют векторную математику, потому что вычисления более просты и менее подвержены особенностям. Сначала это может показаться немного сложным, но как только вы научитесь работать с векторными операциями, многие задачи компьютерной графики станут намного проще.
Позвольте мне объяснить ответ простым способом.
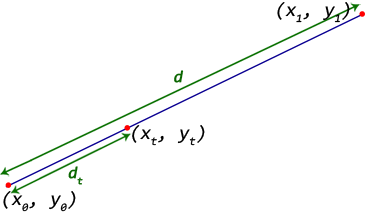
Точка отсчета - (x0, y0)
Конечная точка - (x1, y1)
Нам нужно найти точку (xt, yt) на расстоянии dt от начальной точки к конечной точке.
Расстояние между начальной и конечной точкой определяется как d = sqrt((x1 - x0)^2 + (y1 - y0)^2)
Пусть соотношение расстояний, t = dt / d
Тогда точка (xt, yt) = (((1 - t) * x0 + t * x1), ((1 - t) * y0 + t * y1))
когда 0 < t < 1, точка находится на линии.
когда t < 0точка находится вне линии рядом с (x0, y0),
когда t > 1точка находится вне линии рядом с (x1, y1),
Вот реализация Python для поиска точки на отрезке линии на заданном расстоянии от начальной точки:
import numpy as np
def get_point_on_vector(initial_pt, terminal_pt, distance):
v = np.array(initial_pt, dtype=float)
u = np.array(terminal_pt, dtype=float)
n = v - u
n /= np.linalg.norm(n, 2)
point = v - distance * n
return tuple(point)
На основе отличного ответа @Theophile здесь, на математическом стеке.
Давайте назовем точку, которую вы пытаетесь найти P, с координатами px, py и вашей начальной точкой с координатами ax и ay. Наклон m - это просто отношение изменения Y к изменению X, поэтому, если ваша точка P находится на расстоянии s от A, то ее координаты равны px = ax + s и py = ay + m * s. Теперь, используя Пифагора, расстояние d от A до P будет равно d = sqrt(s * s + (m * s) * (m * s)). Чтобы сделать P определенными единицами D от A, найдите s как s = D/sqrt(1 + m * m).
Я думал, что это было удивительное и простое для понимания решение:
http://www.physicsforums.com/showpost.php?s=f04d131386fbd83b7b5df27f8da84fa1&p=2822353&postcount=4