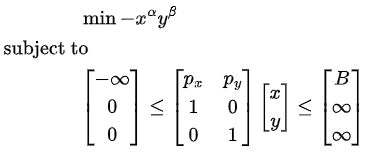Несколько переменных в SciPy's optimize.minimize

Question

Согласно документации SciPy, можно минимизировать функции с несколькими переменными, но это не говорит о том, как оптимизировать такие функции.

from scipy.optimize import minimize
from math import *

def f(c):
  return sqrt((sin(pi/2) + sin(0) + sin(c) - 2)**2 + (cos(pi/2) + cos(0) + cos(c) - 1)**2)

print minimize(f, 3.14/2 + 3.14/7)

Приведенный выше код пытается минимизировать функцию f, но для моей задачи мне нужно минимизировать относительно трех переменных.

Простое введение второго аргумента и настройка минимизации соответственно приводит к ошибке (TypeError: f() takes exactly 2 arguments (1 given)).

Как minimize работать при минимизации с несколькими переменными.

Answer 1

Упакуйте несколько переменных в один массив:

import scipy.optimize as optimize

def f(params):
    # print(params)  # <-- you'll see that params is a NumPy array
    a, b, c = params # <-- for readability you may wish to assign names to the component variables
    return a**2 + b**2 + c**2

initial_guess = [1, 1, 1]
result = optimize.minimize(f, initial_guess)
if result.success:
    fitted_params = result.x
    print(fitted_params)
else:
    raise ValueError(result.message)

доходность

[ -1.66705302e-08  -1.66705302e-08  -1.66705302e-08]

Answer 2

scipy.optimize.minimizeпринимает две обязательные переменные: целевую функцию и начальное предположение переменных целевой функции. Поскольку это итеративный алгоритм, для его сходимости требуется начальное предположение. Таким образом, исходное предположение должно быть обоснованным, иначе алгоритм может не сойтись и/или результаты будут неверными.

Кроме того, если целевая функция использует какие-либо дополнительные аргументы (например, гиперпараметры целевой функции), они не могут быть переданы как kwargs, а должны быть переданы через аргумент (который допускает только кортеж).

Поскольку ОП не имеет целевой функции с несколькими переменными, давайте в качестве иллюстративного примера воспользуемся распространенной экономической проблемой максимизации полезности Кобба-Дугласа .На самом деле это задача максимизации с ограничениями, но поскольку это функция минимизации, ее необходимо привести к задаче минимизации (просто отрицать целевую функцию). Также для того, чтобы передать ограничения какscipy.optimize.LinearConstraintобъект, мы должны написать их так, чтобы они имели нижнюю и верхнюю границы. Таким образом, задача оптимизации выглядит следующим образом:

В этой функции есть две переменные и ; остальные — это все гиперпараметры, которые должны быть предоставлены извне (альфа, бета,px,pyиB). Среди них только альфа и бета являются параметрами целевой функции, поэтому их необходимо передать ей черезargs=аргумент (alphasв примере ниже).

Задача оптимизации решается для и значений, при которых целевая функция достигает своего минимального значения. Как объяснил unutbu , они должны передаваться как один объект (variablesв функции ниже) к целевой функции. Как упоминалось ранее, мы должны сделать обоснованное предположение для этих переменных (xиyцелевой функции) для сходимости алгоритма.

      from scipy.optimize import minimize, LinearConstraint

def obj_func(variables, hyperparams):
    x, y = variables
    alpha, beta = hyperparams
    return - x**alpha * y**beta

B, px, py, alphas = 30, 2, 5, (1/3, 2/3)
linear_constraint = LinearConstraint([[px, py], [1, 0], [0, 1]], [-np.inf, 0, 0], [B, np.inf, np.inf])
result = minimize(obj_func, x0=[1, 1], args=(alphas,), constraints=[linear_constraint])

x_opt, y_opt = result.x     # 4.9996, 4.000
optimum = result.fun        # 4.3088

result.xявляются минимизаторами иresult.funявляется локальным минимумом.

^{Кобб-Дуглас имеет решение в закрытой форме, где для входного примера правильное решение (x_opt, y_opt) = (5, 4). Результат не совсем равен этому, но поскольку minimizeявляется итеративным алгоритмом, он настолько близок к тому, что был до того, как остановился.}