Обнаружение крестов на изображении

Question

Я работаю над программой, чтобы обнаружить наконечники зондирующего устройства и проанализировать изменение цвета во время зондирования. Механизмы ввода / вывода более или менее на месте. То, что мне сейчас нужно, - это фактическое содержание вещей: определение подсказок.

На изображениях ниже подсказки находятся в центре крестов. Я думал о применении BFS к изображениям после некоторого порогового значения, но затем застрял и не знал, как поступить. Затем я обратился к OpenCV после прочтения, что он предлагает функцию обнаружения в изображениях. Тем не менее, я поражен огромным количеством концепций и методов, используемых здесь и снова, не зная, как поступить.

Я смотрю на это правильно? Можете ли вы дать мне несколько советов?

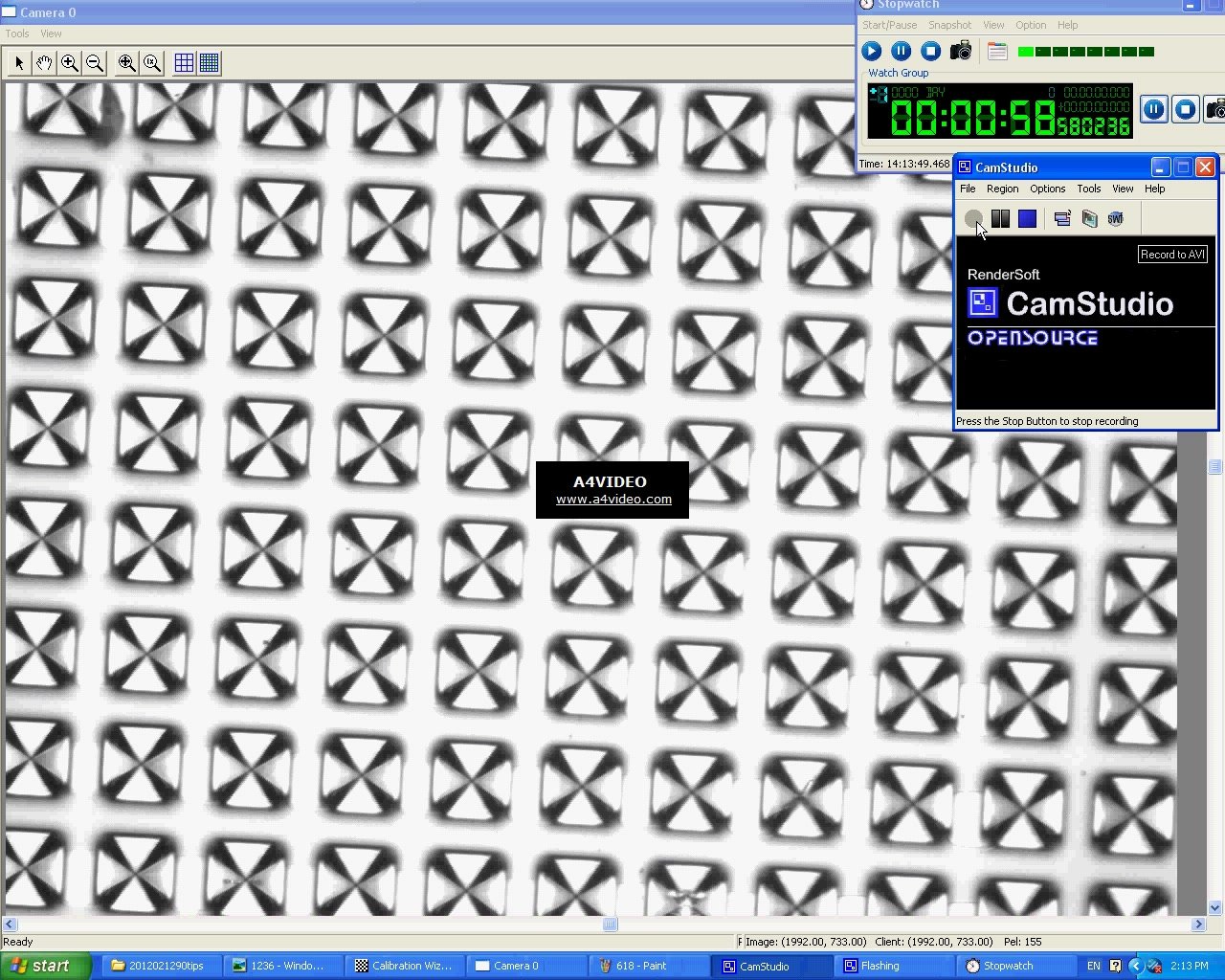Изображение извлечено из короткого видео

Двоичная версия с пороговым значением, установленным на 95

Answer 1

Подход к шаблонам

Вот простое решение matchTemplate, аналогичное подходу, который упоминает Гай Сиртон.

Сопоставление с шаблоном будет работать до тех пор, пока у вас не будет большого масштабирования или поворота с вашей целью.

Вот шаблон, который я использовал:

Вот код, который я использовал для обнаружения нескольких беспрепятственных крестов:

#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <iostream>

using namespace cv;
using namespace std;

int main(int argc, char* argv[])
{
    string inputName = "crosses.jpg";
    string outputName = "crosses_detect.png";
    Mat img   = imread( inputName, 1);
    Mat templ = imread( "crosses-template.jpg", 1);

    int resultCols =  img.cols - templ.cols + 1;
    int resultRows = img.rows - templ.rows + 1;
    Mat result( resultCols, resultRows, CV_32FC1 );

    matchTemplate(img, templ, result, CV_TM_CCOEFF);
    normalize(result, result, 0, 255.0, NORM_MINMAX, CV_8UC1, Mat());

    Mat resultMask;
    threshold(result, resultMask, 180.0, 255.0, THRESH_BINARY);

    Mat temp = resultMask.clone();
    vector< vector<Point> > contours;
    findContours(temp, contours, CV_RETR_EXTERNAL, CV_CHAIN_APPROX_SIMPLE, Point(templ.cols / 2, templ.rows / 2));

    vector< vector<Point> >::iterator i;
    for(i = contours.begin(); i != contours.end(); i++)
    {
        Moments m = moments(*i, false);
        Point2f centroid(m.m10 / m.m00, m.m01 / m.m00);
        circle(img, centroid, 3, Scalar(0, 255, 0), 3);
    }

    imshow("img", img);
    imshow("results", result);
    imshow("resultMask", resultMask);

    imwrite(outputName, img);

    waitKey(0);

    return 0;
}

Это приводит к этому обнаружению изображения: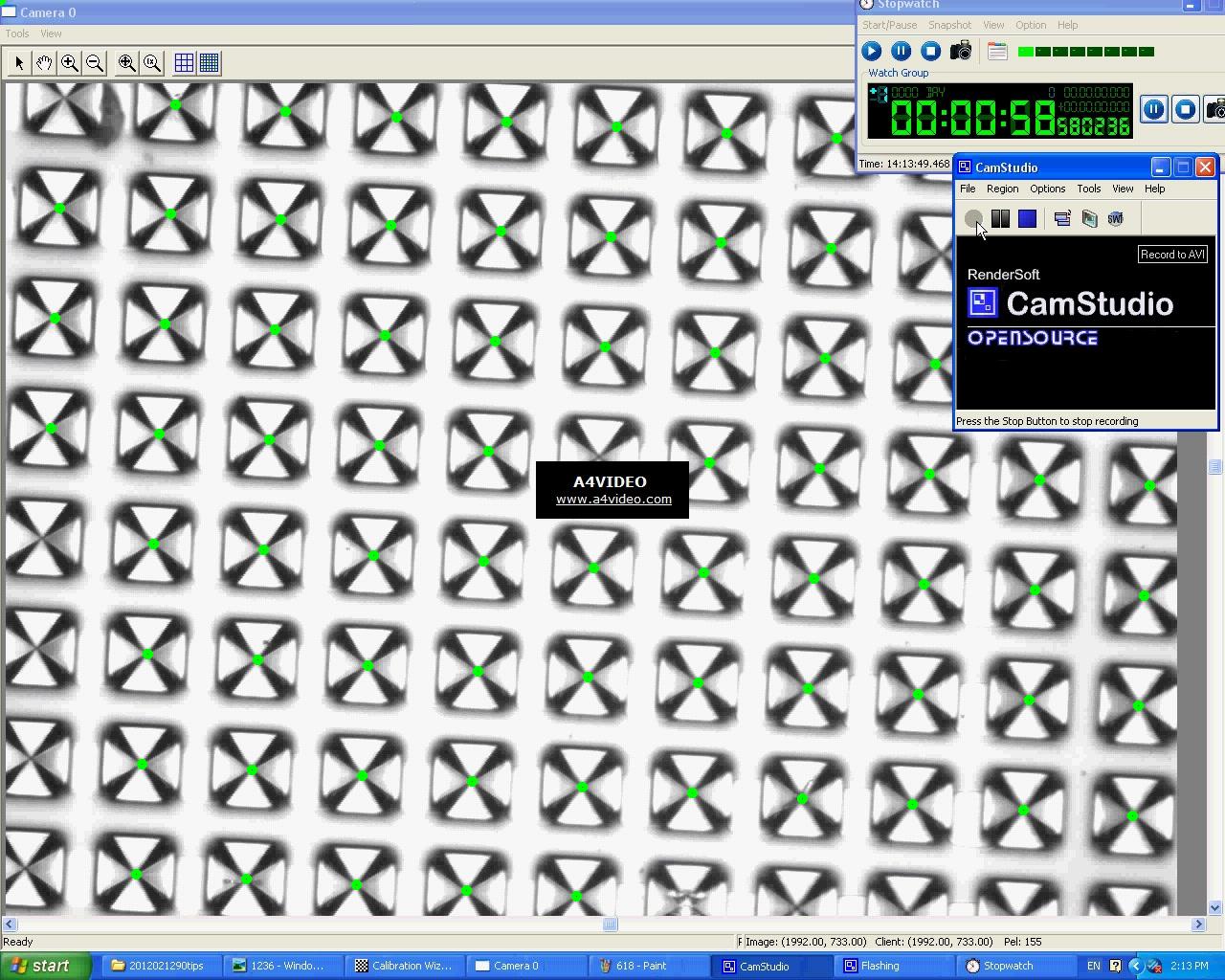

Этот код в основном устанавливает порог, чтобы отделить перекрестные пики от остальной части изображения, а затем обнаруживает все эти контуры. Наконец, он вычисляет центр тяжести каждого контура, чтобы определить центр креста.

Альтернатива обнаружения формы

Вот альтернативный подход с использованием обнаружения треугольника. Это не так точно, как matchTemplate подход, но может быть альтернативой, с которой вы могли бы поиграть.

С помощью findContours мы обнаруживаем все треугольники на изображении, что приводит к следующему:

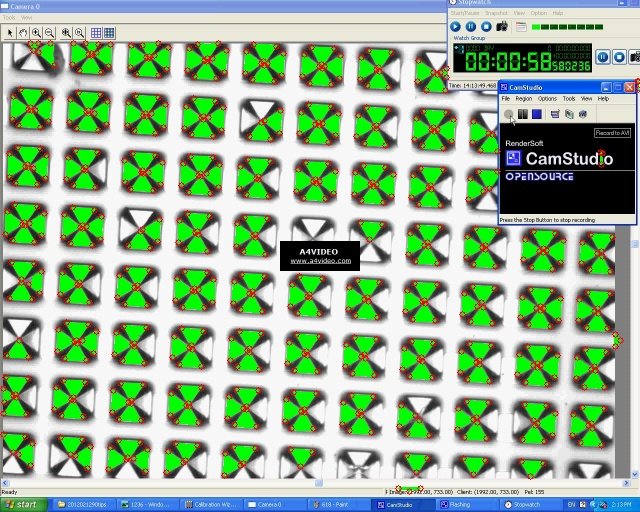
Затем я заметил, что все треугольные вершины кластеризуются вблизи центра пересечения, поэтому эти кластеры используются для центрирования точки пересечения, показанной ниже:

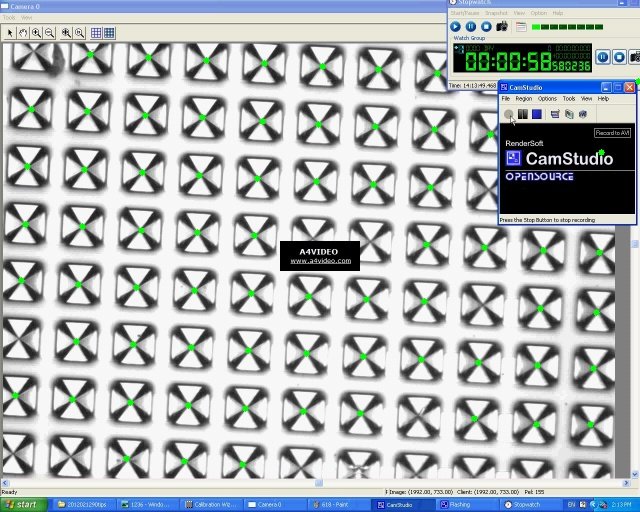
Наконец, вот код, который я использовал для этого:

#include <opencv2/core/core.hpp>
#include <opencv2/highgui/highgui.hpp>
#include <opencv2/imgproc/imgproc.hpp>
#include <iostream>
#include <list>

using namespace cv;
using namespace std;

vector<Point> getAllTriangleVertices(Mat& img, const vector< vector<Point> >& contours);
double euclideanDist(Point a, Point b);

vector< vector<Point> > groupPointsWithinRadius(vector<Point>& points, double radius);
void printPointVector(const vector<Point>& points);
Point computeClusterAverage(const vector<Point>& cluster);

int main(int argc, char* argv[])
{
    Mat img   = imread("crosses.jpg", 1);
    double resizeFactor = 0.5;
    resize(img, img, Size(0, 0), resizeFactor, resizeFactor);

    Mat momentImg = img.clone();

    Mat gray;
    cvtColor(img, gray, CV_BGR2GRAY);

    adaptiveThreshold(gray, gray, 255.0, ADAPTIVE_THRESH_MEAN_C, THRESH_BINARY, 19, 15);
    imshow("threshold", gray);
    waitKey();

    vector< vector<Point> > contours;
    findContours(gray, contours, CV_RETR_LIST, CV_CHAIN_APPROX_SIMPLE);

    vector<Point> allTriangleVertices = getAllTriangleVertices(img, contours);

    imshow("img", img);
    imwrite("shape_detect.jpg", img);
    waitKey();

    printPointVector(allTriangleVertices);
    vector< vector<Point> > clusters = groupPointsWithinRadius(allTriangleVertices, 10.0*resizeFactor);
    cout << "Number of clusters: " << clusters.size() << endl;

    vector< vector<Point> >::iterator cluster;
    for(cluster = clusters.begin(); cluster != clusters.end(); ++cluster)
    {
        printPointVector(*cluster);

        Point clusterAvg = computeClusterAverage(*cluster);
        circle(momentImg, clusterAvg, 3, Scalar(0, 255, 0), CV_FILLED);
    }

    imshow("momentImg", momentImg);
    imwrite("centroids.jpg", momentImg);
    waitKey();

    return 0;
}

vector<Point> getAllTriangleVertices(Mat& img, const vector< vector<Point> >& contours)
{
    vector<Point> approxTriangle;
    vector<Point> allTriangleVertices;
    for(size_t i = 0; i < contours.size(); i++)
    {
        approxPolyDP(contours[i], approxTriangle, arcLength(Mat(contours[i]), true)*0.05, true);
        if(approxTriangle.size() == 3)
        {
            copy(approxTriangle.begin(), approxTriangle.end(), back_inserter(allTriangleVertices));
            drawContours(img, contours, i, Scalar(0, 255, 0), CV_FILLED);

            vector<Point>::iterator vertex;
            for(vertex = approxTriangle.begin(); vertex != approxTriangle.end(); ++vertex)
            {
                circle(img, *vertex, 3, Scalar(0, 0, 255), 1);
            }
        }
    }

    return allTriangleVertices;
}

double euclideanDist(Point a, Point b)
{
    Point c = a - b;
    return cv::sqrt(c.x*c.x + c.y*c.y);
}

vector< vector<Point> > groupPointsWithinRadius(vector<Point>& points, double radius)
{
    vector< vector<Point> > clusters;
    vector<Point>::iterator i;
    for(i = points.begin(); i != points.end();)
    {
        vector<Point> subCluster;
        subCluster.push_back(*i);

        vector<Point>::iterator j;
        for(j = points.begin(); j != points.end(); )
        {
            if(j != i &&  euclideanDist(*i, *j) < radius)
            {
                subCluster.push_back(*j);
                j = points.erase(j);
            }
            else
            {
                ++j;
            }
        }

        if(subCluster.size() > 1)
        {
            clusters.push_back(subCluster);
        }

        i = points.erase(i);
    }

    return clusters;
}

Point computeClusterAverage(const vector<Point>& cluster)
{
    Point2d sum;
    vector<Point>::const_iterator point;
    for(point = cluster.begin(); point != cluster.end(); ++point)
    {
        sum.x += point->x;
        sum.y += point->y;
    }

    sum.x /= (double)cluster.size();
    sum.y /= (double)cluster.size();

    return Point(cvRound(sum.x), cvRound(sum.y));
}

void printPointVector(const vector<Point>& points)
{
    vector<Point>::const_iterator point;
    for(point = points.begin(); point != points.end(); ++point)
    {
        cout << "(" << point->x << ", " << point->y << ")";
        if(point + 1 != points.end())
        {
            cout << ", ";
        }
    }
    cout << endl;
}

Я исправил несколько ошибок в моей предыдущей реализации и немного исправил код. Я также проверил это с различными факторами изменения размера, и это, казалось, работало довольно хорошо. Однако после того, как я достиг четвертой шкалы, у него начались проблемы с правильным определением треугольников, так что это может не сработать для очень маленьких скрещиваний. Кроме того, кажется, есть ошибка в moments функционировать как для некоторых допустимых кластеров, которые он возвращал (-NaN, -NaN) местоположений. Итак, я считаю, что точность немного улучшилась. Возможно, потребуется еще несколько настроек, но в целом я думаю, что это будет хорошей отправной точкой для вас.

Я думаю, что мое обнаружение треугольника работало бы лучше, если бы черная граница вокруг треугольников была немного толще / острее, и если было меньше теней на самих треугольниках.

Надеюсь, это поможет!

Answer 2

Как насчет простого определения автокорреляции, поскольку у вас есть хороший периодический шаблон в ваших изображениях.

Допустим, у вас есть целевое изображение:

И шаблон изображения для синхронизации с

Вы можете определить автокорреляцию обоих:

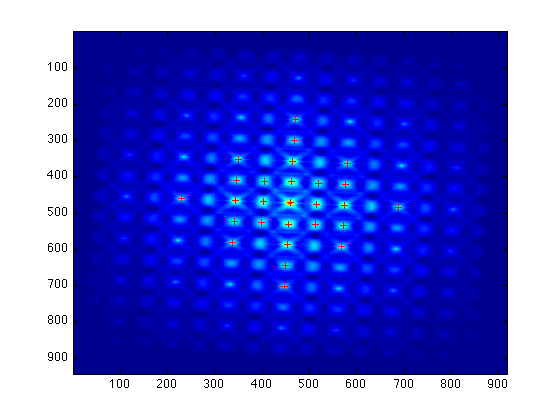
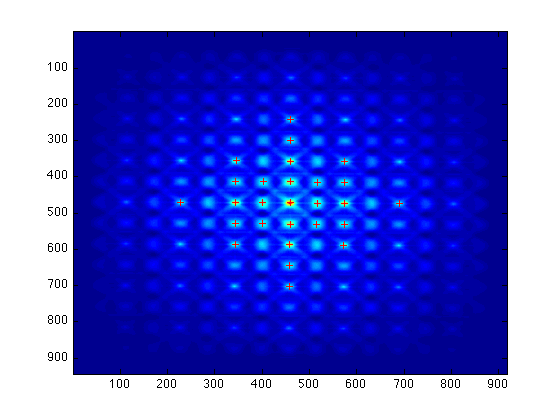
В обоих случаях вы можете обнаружить пики ACF, как в этом примере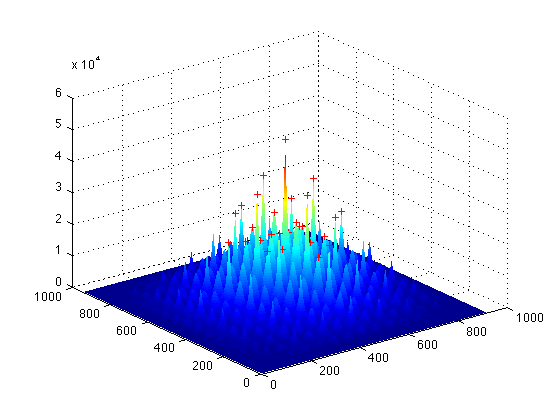

Эти пики вы можете сопоставить друг с другом, используя венгерский алгоритм. Здесь совпадение обозначено белой линией.

Это дает вам набор совпадающих 2D координат, которые, как мы надеемся, удовлетворяют соотношению:

x = Ax'

куда A матрица преобразования с масштабированием и вращением. Решение, таким образом, дает вам поворот и масштабирование между вашим шаблоном и целевым изображением. Затем можно установить перевод с помощью обычной взаимной корреляции с частично исправленным / исправленным изображением и шаблоном изображения.

Answer 3

В прошлом я использовал коммерческий инструмент под названием HexSight ( http://www.lmi3d.com/product/hexsight) в очень похожем приложении. Мы были очень довольны его производительностью и точностью.

Если вы ищете что-то очень грубое / базовое, вы можете попытаться вычислить взаимную корреляцию между опорным изображением и изображением, на которое вы смотрите. Альтернатива (которую использует HexSight) состоит в том, чтобы начать с некоторого алгоритма обнаружения краев, прежде чем пытаться найти совпадения с эталонным изображением. В любом случае вы можете использовать некоторый алгоритм уточнения, когда у вас есть приблизительный кандидат. Учитывая, что вы пытаетесь найти какой-то конкретный тип цели, вы можете применить эвристику или воспользоваться конкретной целью с помощью специального алгоритма.

Вот идея для пользовательского решения, предполагая, что кресты равномерно распределены по сетке, и изображение не слишком искажено:

• Суммируйте все строки и столбцы изображения. Это создаст пики между строками и столбцами крестиков (которые белого цвета).
• Определите поворот изображения путем поиска угла, который максимизирует ширину и амплитуду этих пиков. Вы можете выполнить бинарный поиск между +/- вашим максимальным ожидаемым углом.
• После того, как вы определили угол, теперь вы можете использовать центральные линии пиков, чтобы определить местоположение зондов. На самом деле у вас будет еще один узкий / меньший пик прямо вокруг центра целей.

Согласно предположениям, это должно быть достаточно надежным и точным, поскольку он использует информацию всего изображения. Он не будет слишком чувствительным к каким-либо локальным проблемам, он даже будет работать, если цель (или несколько) полностью отсутствует или скрыта.

Хорошая оптика и освещение - необходимые условия для получения высококачественных результатов из любой системы. Изображение, к которому вы привязываетесь, выглядит не очень хорошо.