Применение idwt2 в MATLAB несколько раз
Я использую MATLAB для применения дискретного вейвлет-преобразования к изображению. Я применяю его несколько раз (3), чтобы получить 3-х уровневое преобразование. Я использую dwt2 функция, предоставляемая MATLAB для сжатия и idwt2 сделать декомпрессию. Проблема в том, что я не знаю, как распаковать несколько раз, как в применении idwt2 несколько раз к предыдущему полученному выводу, так как он возвращает матрицу. Взять, к примеру:
x = idwt2(scaled3, vertical3, horizontal3, diagonal3, Lo_R, Ho_R);
Как должен idwt2 быть применены к х?
2 ответа
Глядя на документацию для dwt2 а также idwt2 Похоже, у вас есть 2 основных варианта восстановления ваших многократно разложенных изображений:
- Сохраните все матрицы коэффициентов детализации по горизонтали, вертикали и диагонали на каждом этапе декомпозиции и используйте их при реконструкции.
- Введите пустую матрицу (
[]) для любых матриц коэффициентов детализации, которые вы не сохранили из предыдущих этапов декомпозиции.
Поскольку это был медленный день, вот некоторый код, показывающий, как это сделать и как выглядят результаты для каждого случая...
Сначала загрузите образец изображения и инициализируйте некоторые переменные:
load woman; % Load image data
nLevel = 3; % Number of decompositions
nColors = size(map, 1); % Number of colors in colormap
cA = cell(1, nLevel); % Approximation coefficients
cH = cell(1, nLevel); % Horizontal detail coefficients
cV = cell(1, nLevel); % Vertical detail coefficients
cD = cell(1, nLevel); % Diagonal detail coefficients
Теперь примените декомпозиции (в данном случае 3) и сохраните матрицы коэффициентов детализации для каждого шага в массиве ячеек:
startImage = X;
for iLevel = 1:nLevel,
[cA{iLevel}, cH{iLevel}, cV{iLevel}, cD{iLevel}] = dwt2(startImage, 'db1');
startImage = cA{iLevel};
end
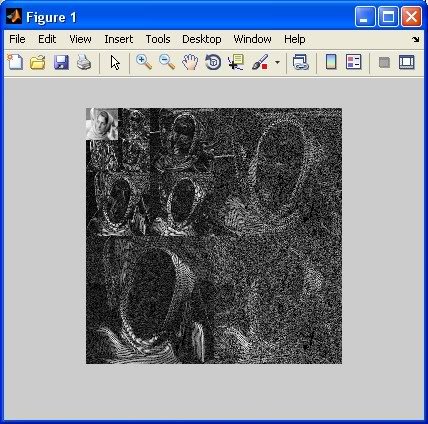
Чтобы увидеть, как будет выглядеть окончательное разложенное изображение, вместе со всеми матрицами коэффициентов детализации, запустите следующий код (который использует wcodemat):
tiledImage = wcodemat(cA{nLevel}, nColors);
for iLevel = nLevel:-1:1,
tiledImage = [tiledImage wcodemat(cH{iLevel}, nColors); ...
wcodemat(cV{iLevel}, nColors) wcodemat(cD{iLevel}, nColors)];
end
figure;
imshow(tiledImage, map);
Вы должны увидеть что-то вроде этого:
Теперь пришло время восстановить! Следующий код выполняет "полную" реконструкцию (используя все сохраненные матрицы коэффициентов детализации) и "частичную" реконструкцию (не используя ни одну из них), а затем строит изображения:
fullRecon = cA{nLevel};
for iLevel = nLevel:-1:1,
fullRecon = idwt2(fullRecon, cH{iLevel}, cV{iLevel}, cD{iLevel}, 'db1');
end
partialRecon = cA{nLevel};
for iLevel = nLevel:-1:1,
partialRecon = idwt2(partialRecon, [], [], [], 'db1');
end
figure;
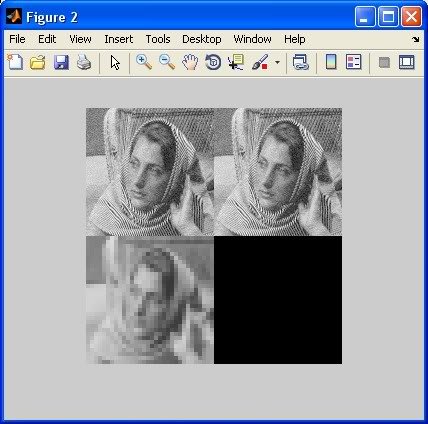
imshow([X fullRecon; partialRecon zeros(size(X))], map, ...
'InitialMagnification', 50);
Обратите внимание, что исходная (вверху слева) и "полная" реконструкция (вверху справа) выглядят неразличимо, но "частичная" реконструкция (внизу слева) очень пикселизирована. Разница не будет такой серьезной, если вы примените меньше шагов разложения, например, 1 или 2.
% Multi-level reconstruction from DWT coefficients
% The variable "coefs" is what you get when you perform forward dwt2()
% on the image you're decomposing. It is a long row
% vector that has cA- approximation details, cH -horizontal details, cV-
% vertical details, cD-diagonal details
L=3; % For db 3-level reconstruction for example
k=size(image,1)/2^L; % I am assuming a square sized image where both
% dimensions are equal
for level=0:(L-1)
s=k*2^level;
if level==0
cA=reshape(coefs(1,1:s^2),s,s);
figure;imshow(cA,[])
end
cH=reshape(coefs(1,(s^2+1):2*s^2),s,s);
figure;imshow(cH,[])
cV=reshape(coefs(1,(2*s^2+1):3*s^2),s,s);
figure;imshow(cV,[])
cD=reshape(coefs(1,(3*s^2+1):4*s^2),s,s);
figure;imshow(cD,[])
I_rec=idwt2(cA,cH,cV,cD,"db1");
figure;imshow(I_rec,[])
cA=I_rec; % The recosntructed image is the approximation detail-cA
% for next levels of reconstruction
end