Выбор размера мини-пакета для регрессии нейронной сети

Question

Я делаю регрессию нейронной сети с 4 функциями. Как определить размер мини-партии для моей проблемы? Я вижу, что люди используют размер пакета 100-1000 для компьютерного зрения с 32*32*3 функциями для каждого изображения, означает ли это, что я должен использовать размер пакета 1 миллион? У меня есть миллиарды данных и десятки гигабайт памяти, поэтому для меня нет строгих требований не делать этого.

Я также заметил, что использование мини-партии размером ~ 1000 делает конвергенцию намного быстрее, чем размер партии в 1 миллион. Я думал, что должно быть наоборот, так как градиент, рассчитанный с большим размером партии, является наиболее представительным для градиента всей выборки? Почему использование мини-пакета ускоряет конвергенцию?

Answer 1

От размера пакета Tradeoff против количества итераций для обучения нейронной сети:

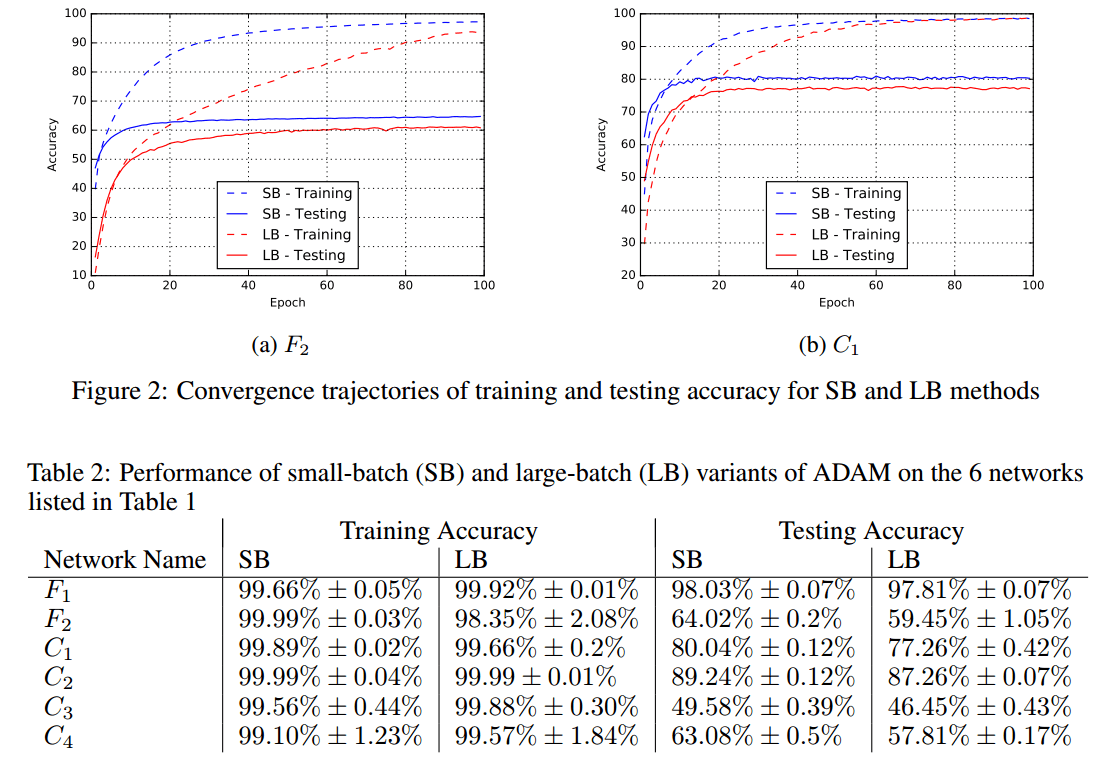
Из Нитиш Шириш Кескар, Дхиватса Мудигере, Хорхе Носедал, Михаила Смелянского, Пинг Так Питер Танг. О крупномасштабном обучении для глубокого обучения: разрыв в обобщении и острые минимумы. https://arxiv.org/abs/1609.04836:

Метод стохастического градиентного спуска и его варианты являются алгоритмами выбора для многих задач глубокого обучения. Эти методы работают в режиме малой партии, когда часть обучающих данных, обычно 32-512 точек данных, отбирается для вычисления приближения к градиенту. На практике наблюдалось, что при использовании более крупной партии качество модели значительно ухудшается, что измеряется ее способностью к обобщению. Были предприняты некоторые попытки исследовать причину такого обобщения в режиме больших партий, однако точный ответ для этого явления до сих пор неизвестен. В этой статье мы представляем достаточно числовых доказательств, подтверждающих мнение о том, что методы больших партий имеют тенденцию сходиться к точным минимизаторам функций обучения и тестирования - и что острые минимумы приводят к худшему обобщению. Напротив, мелкосерийные методы постоянно сходятся к плоским минимизаторам, и наши эксперименты подтверждают широко распространенное мнение о том, что это происходит из-за собственного шума при оценке градиента. Мы также обсуждаем несколько эмпирических стратегий, которые помогают методам больших партий устранить пробел в обобщении и завершить с набором будущих идей исследования и открытых вопросов.

[...]

Отсутствие способности к обобщению связано с тем, что методы больших партий имеют тенденцию сходиться к резким минимизаторам обучающей функции. Эти минимизаторы характеризуются большими положительными собственными значениями в $\nabla^2 f(x)$ и имеют тенденцию обобщать менее хорошо. Напротив, мелкосерийные методы сходятся к плоским минимизаторам, характеризующимся небольшими положительными собственными значениями $\nabla^2 f(x)$. Мы наблюдали, что ландшафт функций потерь глубоких нейронных сетей таков, что методы больших партий почти неизменно притягиваются к областям с резкими минимумами и что, в отличие от методов небольших партий, не могут покинуть бассейны этих минимизаторов.

[...]

Кроме того, несколько хороших идей от Яна Гудфеллоу, отвечающих на вопрос, почему не использовать весь тренировочный набор для вычисления градиента? на Quora:

Размер скорости обучения ограничен, в основном, такими факторами, как степень изогнутости функции стоимости. Вы можете думать о градиентном спуске как о линейном приближении к функции стоимости, а затем о движении вниз по этой приблизительной стоимости. Если функция стоимости сильно нелинейна (сильно изогнута), то аппроксимация не будет очень хорошей для очень большого расстояния, поэтому безопасны только небольшие размеры шагов. Вы можете прочитать больше об этом в Главе 4 учебника по углубленному обучению по численным вычислениям: http://www.deeplearningbook.org/contents/numerical.html

Когда вы помещаете m примеров в мини-пакет, вам необходимо выполнить O(m) вычисления и использовать O(m) память, но вы уменьшаете количество неопределенности в градиенте только в O(sqrt(m)). Другими словами, снижается предельная отдача от размещения большего количества примеров в мини-пакете. Подробнее об этом вы можете прочитать в главе 8 учебника по углубленному обучению об алгоритмах оптимизации для глубокого обучения: http://www.deeplearningbook.org/contents/optimization.html

Кроме того, если вы подумаете об этом, даже использование всего тренировочного набора не даст вам истинного градиента. Истинным градиентом будет ожидаемый градиент с учетом всех возможных примеров, взвешенных по распределению, генерирующему данные. Использование всего обучающего набора - это просто использование очень большого размера мини-пакета, когда размер мини-пакета ограничен суммой, которую вы тратите на сбор данных, а не суммой, которую вы тратите на вычисления.