Генерация скользящего движения с использованием магического битборда
Это вопрос, касающийся общей картины того, как проверить ход скользящей фигуры в шахматах, используя магические битборды. Просто чтобы уточнить, я не спрашиваю, как магические битборды работают внутри.
Теперь немного подробнее по этому вопросу. Я пишу представление шахматной доски, используя битборд, и я хочу проверить ходы скользящих фигур, используя магические битборды. Может кто-нибудь перечислить основные шаги, как этого добиться? В качестве примера рассмотрим следующую позицию доски:
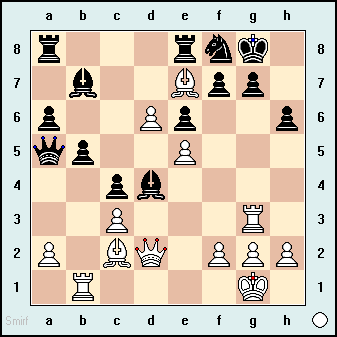
Предположим, у нас есть все магические функции и структуры данных, инициализированные и готовые к использованию. Таким образом, используя только сигнатуры функций для магических битбордов, можете ли вы перечислить шаги (псевдокод или любой язык), чтобы проверить заданный ход для белой ладьи на g3?
3 ответа
Хорошо, что мы можем предположить, что доступны магические функции битовой доски, но в целом функции генерации перемещения битовой доски могут принимать любую технику, которая создает битовую доску, которая дает возможные квадраты для перехода. Сказать RookMoves Если вы используете такую функцию, вы должны заполнить список перемещений следующим образом:
UInt64 pieceBitboard = Bitboard[SideToMove | Piece.Rook];
UInt64 targetBitboard = ~Bitboard[SideToMove | Piece.All];
while (pieceBitboard != 0) {
Int32 from = Bit.Pop(ref pieceBitboard);
UInt64 moveBitboard = targetBitboard & RookMoves(from, OccupiedBitboard);
while (moveBitboard != 0) {
Int32 to = Bit.Pop(ref moveBitboard);
moveList[index++] = Move.Create(this, from, to);
}
}
где Bit.Pop(ref x) возвращает наименее значимый бит в x в то же время "высовывая" (удаляя) его из x,
Чтобы проверить ход (я интерпретирую это как подтверждение правильности хода), вы должны либо проверить, есть ли этот шаг в списке ходов, либо выполнить ход и посмотреть, оставит ли он вас под контролем. Конечно, вам может понадобиться проверить, подчиняется ли оно правилам перемещения фигуры, но это тривиально.
if ((RookRays[move.From] & Bit.At[move.To]) == 0)
return false;
Int32 side = SideToMove;
position.Make(move);
Boolean valid = position.InCheck(side);
position.Unmake(move);
return valid;
Проще говоря, волшебные битборды - эффективный способ занять позицию и получить легальные ходы для скользящей фигуры.
Во-первых, вам нужно найти магические числа. Часть кода, который вы пишете, чтобы найти магические числа, также будет повторно использоваться при использовании магических чисел.
Для начала вам нужно написать 5 функций. Они не должны быть особенно быстрыми, потому что вы будете использовать их только при поиске магических чисел и один раз при запуске программы, прежде чем использовать свои магические числа. Вы можете использовать любую старую технику в этих функциях.
uint64_t blockermask_rook (int square);
uint64_t blockermask_bishop (int square);
uint64_t moveboard_rook (int square, uint64_t blockerboard);
uint64_t moveboard_bishop (int square, uint64_t blockerboard);
uint64_t blockerboard (int index, uint64_t blockermask);
Таким образом, вы можете спросить себя: а есть ли маска блокировщика, доска перемещения и доска блокировщика? Ну, я только что придумал условия, но вот что я имею в виду под ними:
/* Example, Rook on e4:
*
* The blocker mask A blocker board The move board
* 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
* 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
* 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
* 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0
* 0 1 1 1 0 1 1 0 0 1 1 0 0 0 0 0 0 0 1 1 0 1 1 1
* 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0
* 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0
* 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
*/
Маска блокиратора - это все квадраты, которые могут быть заняты и блокируют вашу фигуру от дальнейшего продвижения. Квадраты не обязательно должны быть частью этого, потому что ваша фигура не может пройти дальше этого квадрата в любом случае. Количество единиц в этой битовой доске определяет, какой размер таблицы поиска вам нужен для этой комбинации фигуры и квадрата. В этом случае их 10, поэтому есть 2^10 (1024) возможных перестановок фигур, которые могут заблокировать ладью e4.
Блокаторная доска - одна из этих перестановок. В этом примере есть части на b4, c4, e2, e5 и e7. Это вражеские и дружелюбные фигуры. Доска блокировщика всегда является подмножеством маски блокировщика (на ней не обязательно показывать фигуры на других клетках (например, blockers = occupancy & blockermask;)).
Доска ходов - это итоговые доступные ходы для вашей фигуры, для данной доски блокировщиков. Это включает в себя возможные захваты для вашего произведения. Обратите внимание, что это также включает в себя захват ваших собственных фигур (но вы можете просто И это с НЕ из ваших собственных мест расположения штук, чтобы удалить их).
Итак, в основном вам нужно сгенерировать маску блокировщика на всех клетках, как для ладьи, так и для слона. И вам также нужно создать все возможные блокирующие доски на каждом квадрате, как для ладьи, так и для слона. Когда вы генерируете доски блокировщиков, вы также должны генерировать получившиеся доски движений. Храните все эти вещи в массивах для последующего использования.
Теперь, когда вы это сделали, для каждой комбинации квадрата / фигуры вы пытаетесь выбрать случайные 64-битные числа и посмотреть, являются ли они магическими. Вы узнаете, волшебны ли они, используя волшебную формулу, return ((blockerboard*magic) >> (64-bits));, который создаст магический индекс из 0..2^ бит (0..1024 в случае ладьи е4). Для определенной фигуры / квадрата, если две доски блокировщиков когда-либо генерируют один и тот же магический индекс, но эти две доски блокировок имеют разные доски перемещения, то это число магглов, и вам следует попробовать новый.
Как только вы это сделаете, у вас будет 64 магических номера ладьи и 64 магических числа слона. Чтобы использовать их, при запуске программы вы инициализируете все маски блокировщиков, доски блокировщиков и перемещайте доски. И теперь ваша программа может эффективно искать доски ходов для слонов и грачей на любом квадрате (и, следовательно, также на ферзях). Код для этого будет выглядеть примерно так:
/* Retrieves the move board for the given square and occupancy board. */
uint64_t magic_move_rook (int8_t square, uint64_t occupancy)
{
/* Remove occupants that aren't in the blocker mask for this square. */
occupancy &= Rook.blockmask[square];
/* Calculate the magic move index. */
int index = (occupancy*Rook.magic[square]) >> (64-Rook.bits[square]);
/* Return the pre-calculated move board. */
return Rook.moveboard[square][index];
}
Хаха, никогда не слышал о "волшебной доске". Google это, и это именно то, что я ожидал. Хотя я не вижу в этом никакой магии. В любом случае, чтобы ответить на ваш вопрос, вам нужно сгенерировать доступную позицию бита перемещения текущего выбранного фрагмента. Не уверен, что еще нужно.
Что касается кода psuedo что-то вроде так, я думаю:
Positions KingChessPiece::getMovablePositions(){
(x,y) = current bit position in the bitboard
availablePosition = [ (x+1,y),(x-1,y),(x,y+1),(x,y-1) ]
for each position in availablePosition
if p_i is occupied then remove it from list
return availablePosition
}
Я имею в виду, что в этом нет ничего сложного, вам просто нужно убедиться, что вы получаете и устанавливаете положение таким образом, чтобы это было совместимо с внутренней структурой, которую вы используете.
РЕДАКТИРОВАТЬ:
пример королевы:
Position QueenChessPiece::getMovablePosition(){
(x,y) = queens current position
availablePosition = []; //empty list
//check diagonal positions
//move top left diagonal
availablePosition.concat( this.generateAvailablePosition(x,y,-1,1);
//move top right diagonal
availablePosition.concat( this.generateAvailablePosition(x,y,1,1);
//move bottom right diagonal
availablePosition.concat( this.generateAvailablePosition(x,y,1,-1);
//move bottom left diagonal
availablePosition.concat( this.generateAvailablePosition(x,y,-1,-1);
//move straight up
availablePosition.concat( this.generateAvailablePosition(x,y,0,1) )
//move straight down
availablePosition.concat( this.generateAvailablePosition(x,y,0,-1) )
//move left
availablePosition.concat( this.generateAvailablePosition(x,y,-1,0) )
//move right
availablePosition.concat( this.generateAvailablePosition(x,y,1,0) )
return availablePosition;
}
Position QueenChess::generateAvailablePosition(x,y,dx,dy){
availPosition = [];
while( !isSpaceOccupied(x + dx , y + dy))
availPosition.add( position(x + dx ,y + dy) );
x += dx;
y += dy;
endWhile
return availPosition;
}