Нахождение локальных максимумов и минимумов
Я ищу эффективный в вычислительном отношении способ найти локальные максимумы / минимумы для большого списка чисел в R. Надеюсь, без for петли...
Например, если у меня есть файл данных, как 1 2 3 2 1 1 2 1Я хочу, чтобы функция возвращала 3 и 7, которые являются позициями локальных максимумов.
17 ответов
diff(diff(x)) (или же diff(x,differences=2): спасибо @ZheyuanLi) по существу вычисляет дискретный аналог второй производной, поэтому должен быть отрицательным при локальных максимумах. +1 ниже заботится о том, что результат diff короче, чем входной вектор.
edit: добавлена коррекция @Tommy для случаев, когда delta-x не равен 1...
tt <- c(1,2,3,2,1, 1, 2, 1)
which(diff(sign(diff(tt)))==-2)+1
Мое предложение выше ( http://statweb.stanford.edu/~tibs/PPC/Rdist/) предназначено для случая, когда данные являются более шумными.
Решение @ Бена довольно милое. Это не обрабатывает следующие случаи, хотя:
# all these return numeric(0):
x <- c(1,2,9,9,2,1,1,5,5,1) # duplicated points at maxima
which(diff(sign(diff(x)))==-2)+1
x <- c(2,2,9,9,2,1,1,5,5,1) # duplicated points at start
which(diff(sign(diff(x)))==-2)+1
x <- c(3,2,9,9,2,1,1,5,5,1) # start is maxima
which(diff(sign(diff(x)))==-2)+1
Вот более надежная (и более медленная, уродливая) версия:
localMaxima <- function(x) {
# Use -Inf instead if x is numeric (non-integer)
y <- diff(c(-.Machine$integer.max, x)) > 0L
rle(y)$lengths
y <- cumsum(rle(y)$lengths)
y <- y[seq.int(1L, length(y), 2L)]
if (x[[1]] == x[[2]]) {
y <- y[-1]
}
y
}
x <- c(1,2,9,9,2,1,1,5,5,1)
localMaxima(x) # 3, 8
x <- c(2,2,9,9,2,1,1,5,5,1)
localMaxima(x) # 3, 8
x <- c(3,2,9,9,2,1,1,5,5,1)
localMaxima(x) # 1, 3, 8
Используйте функцию zoo library rollapply:
x <- c(1, 2, 3, 2, 1, 1, 2, 1)
library(zoo)
xz <- as.zoo(x)
rollapply(xz, 3, function(x) which.min(x)==2)
# 2 3 4 5 6 7
#FALSE FALSE FALSE TRUE FALSE FALSE
rollapply(xz, 3, function(x) which.max(x)==2)
# 2 3 4 5 6 7
#FALSE TRUE FALSE FALSE FALSE TRUE
Затем извлеките индекс, используя "coredata" для тех значений, где "which.max" является "центральным значением", сигнализирующим о локальном максимуме. Очевидно, вы могли бы сделать то же самое для локальных минимумов, используя which.min вместо which.max,
rxz <- rollapply(xz, 3, function(x) which.max(x)==2)
index(rxz)[coredata(rxz)]
#[1] 3 7
Я предполагаю, что вам не нужны начальные или конечные значения, но если вы захотите, вы можете дополнить концы своих векторов перед обработкой, как это делают теломеры на хромосомах.
(Я отмечаю пакет ppc ("Пиковые контрасты вероятности") для проведения масс-спектрометрического анализа, просто потому, что я не знал о его доступности до прочтения комментария @BenBolker выше, и я думаю, что добавление этих нескольких слов увеличит шансы того, что кто-то с массовый интерес увидит это в поиске.)
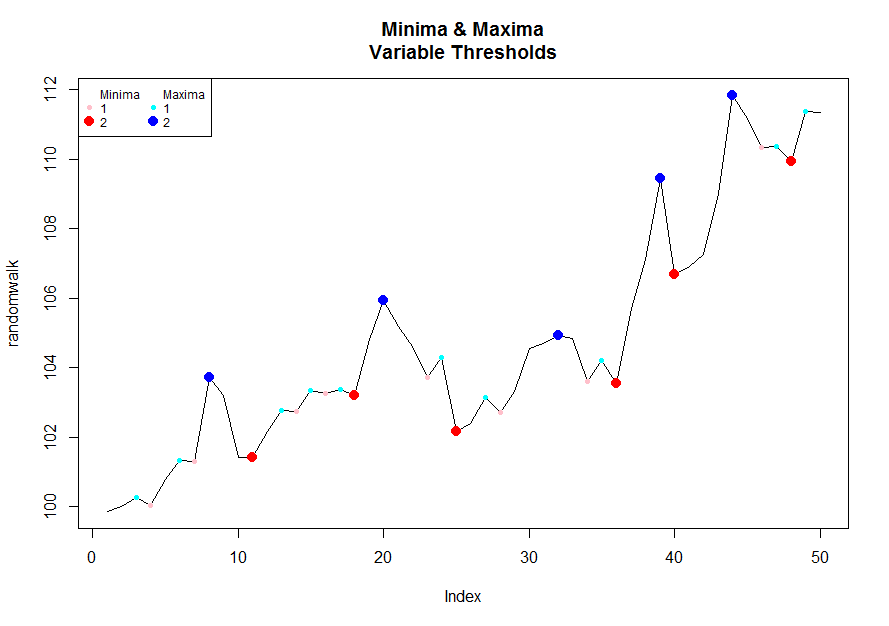
Я сделал удар сегодня. Я знаю, что вы сказали, надеюсь, без циклов for, но я придерживался с помощью функции apply. Несколько компактный и быстрый и позволяет задавать пороговое значение, чтобы вы могли превысить 1.
Функция:
inflect <- function(x, threshold = 1){
up <- sapply(1:threshold, function(n) c(x[-(seq(n))], rep(NA, n)))
down <- sapply(-1:-threshold, function(n) c(rep(NA,abs(n)), x[-seq(length(x), length(x) - abs(n) + 1)]))
a <- cbind(x,up,down)
list(minima = which(apply(a, 1, min) == a[,1]), maxima = which(apply(a, 1, max) == a[,1]))
}
Чтобы визуализировать его / играть с порогами, вы можете запустить следующий код:
# Pick a desired threshold # to plot up to
n <- 2
# Generate Data
randomwalk <- 100 + cumsum(rnorm(50, 0.2, 1)) # climbs upwards most of the time
bottoms <- lapply(1:n, function(x) inflect(randomwalk, threshold = x)$minima)
tops <- lapply(1:n, function(x) inflect(randomwalk, threshold = x)$maxima)
# Color functions
cf.1 <- grDevices::colorRampPalette(c("pink","red"))
cf.2 <- grDevices::colorRampPalette(c("cyan","blue"))
plot(randomwalk, type = 'l', main = "Minima & Maxima\nVariable Thresholds")
for(i in 1:n){
points(bottoms[[i]], randomwalk[bottoms[[i]]], pch = 16, col = cf.1(n)[i], cex = i/1.5)
}
for(i in 1:n){
points(tops[[i]], randomwalk[tops[[i]]], pch = 16, col = cf.2(n)[i], cex = i/1.5)
}
legend("topleft", legend = c("Minima",1:n,"Maxima",1:n),
pch = rep(c(NA, rep(16,n)), 2), col = c(1, cf.1(n),1, cf.2(n)),
pt.cex = c(rep(c(1, c(1:n) / 1.5), 2)), cex = .75, ncol = 2)
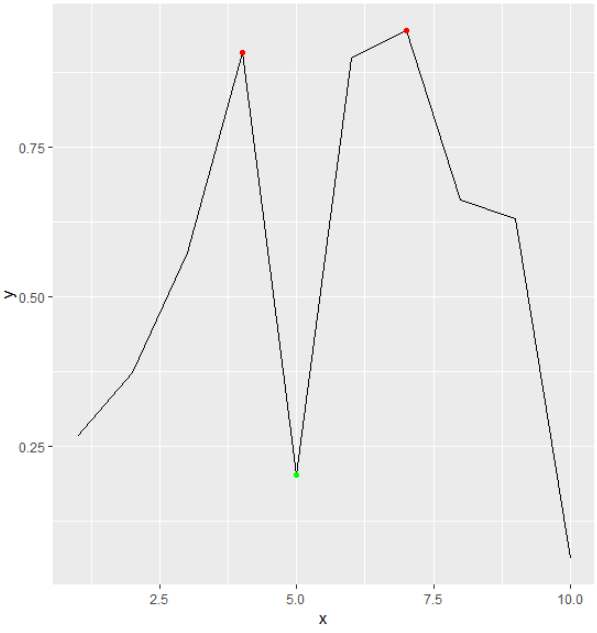
Поздно на вечеринку, но это может быть интересно другим. В настоящее время вы можете использовать (внутреннюю) функциюfind_peaks от ggpmiscпакет. Вы можете параметризовать его, используяthreshold, span а также strictаргументы. посколькуggpmisc пакет предназначен для использования с ggplot2вы можете напрямую построить минимумы и максимумы, используяstat_peaks а также stat_valleys функции:
set.seed(1)
x <- 1:10
y <- runif(10)
# Maxima
x[ggpmisc:::find_peaks(y)]
[1] 4 7
y[ggpmisc:::find_peaks(y)]
[1] 0.9082078 0.9446753
# Minima
x[ggpmisc:::find_peaks(-y)]
[1] 5
y[ggpmisc:::find_peaks(-y)]
[1] 0.2016819
# Plot
ggplot(data = data.frame(x, y), aes(x = x, y = y)) + geom_line() + stat_peaks(col = "red") + stat_valleys(col = "green")
Есть несколько хороших решений, но это зависит от того, что вам нужно.
Просто diff(tt) возвращает различия.
Вы хотите определить, когда вы переходите от увеличения значений к уменьшению значений. Один из способов сделать это - @Ben:
diff(sign(diff(tt)))==-2
Проблема здесь состоит в том, что это будет обнаруживать только те изменения, которые немедленно переходят от строго возрастающих к строго уменьшающимся.
Небольшое изменение позволит повторить значения на пике (возвращение TRUE для последнего появления пикового значения):
diff(diff(x)>=0)<0
Затем вам просто нужно правильно заполнить переднюю и заднюю части, если вы хотите обнаружить максимумы в начале или в конце
Вот все, что входит в функцию (включая поиск долин):
which.peaks <- function(x,partial=TRUE,decreasing=FALSE){
if (decreasing){
if (partial){
which(diff(c(FALSE,diff(x)>0,TRUE))>0)
}else {
which(diff(diff(x)>0)>0)+1
}
}else {
if (partial){
which(diff(c(TRUE,diff(x)>=0,FALSE))<0)
}else {
which(diff(diff(x)>=0)<0)+1
}
}
}
Ответ @42- это здорово, но у меня был случай, когда я не хотел использовать zoo, Это легко реализовать с помощью dplyr с помощью lag а также lead:
library(dplyr)
test = data_frame(x = sample(1:10, 20, replace = TRUE))
mutate(test, local.minima = if_else(lag(x) > x & lead(x) > x, TRUE, FALSE)
Словно rollapply Решение, вы можете контролировать размер окна и крайние случаи с помощью lag/lead аргументы n а также defaultсоответственно.
In the case I'm working on, duplicates are frequent. So I have implemented a function that allows finding first or last extrema (min or max):
locate_xtrem <- function (x, last = FALSE)
{
# use rle to deal with duplicates
x_rle <- rle(x)
# force the first value to be identified as an extrema
first_value <- x_rle$values[1] - x_rle$values[2]
# differentiate the series, keep only the sign, and use 'rle' function to
# locate increase or decrease concerning multiple successive values.
# The result values is a series of (only) -1 and 1.
#
# ! NOTE: with this method, last value will be considered as an extrema
diff_sign_rle <- c(first_value, diff(x_rle$values)) %>% sign() %>% rle()
# this vector will be used to get the initial positions
diff_idx <- cumsum(diff_sign_rle$lengths)
# find min and max
diff_min <- diff_idx[diff_sign_rle$values < 0]
diff_max <- diff_idx[diff_sign_rle$values > 0]
# get the min and max indexes in the original series
x_idx <- cumsum(x_rle$lengths)
if (last) {
min <- x_idx[diff_min]
max <- x_idx[diff_max]
} else {
min <- x_idx[diff_min] - x_rle$lengths[diff_min] + 1
max <- x_idx[diff_max] - x_rle$lengths[diff_max] + 1
}
# just get number of occurences
min_nb <- x_rle$lengths[diff_min]
max_nb <- x_rle$lengths[diff_max]
# format the result as a tibble
bind_rows(
tibble(Idx = min, Values = x[min], NB = min_nb, Status = "min"),
tibble(Idx = max, Values = x[max], NB = max_nb, Status = "max")) %>%
arrange(.data$Idx) %>%
mutate(Last = last) %>%
mutate_at(vars(.data$Idx, .data$NB), as.integer)
}
The answer to the original question is:
> x <- c(1, 2, 3, 2, 1, 1, 2, 1)
> locate_xtrem(x)
# A tibble: 5 x 5
Idx Values NB Status Last
<int> <dbl> <int> <chr> <lgl>
1 1 1 1 min FALSE
2 3 3 1 max FALSE
3 5 1 2 min FALSE
4 7 2 1 max FALSE
5 8 1 1 min FALSE
Результат показывает, что второй минимум равен 1 и что это значение повторяется дважды, начиная с индекса 5. Таким образом, можно получить другой результат, указав это время функции для поиска последних вхождений локальных экстремумов:
> locate_xtrem(x, last = TRUE)
# A tibble: 5 x 5
Idx Values NB Status Last
<int> <dbl> <int> <chr> <lgl>
1 1 1 1 min TRUE
2 3 3 1 max TRUE
3 6 1 2 min TRUE
4 7 2 1 max TRUE
5 8 1 1 min TRUE
В зависимости от цели затем можно переключаться между первым и последним значением локальных экстремумов. Второй результат сlast = TRUE также можно получить с помощью операции между столбцами "Idx" и "NB"...
Наконец, чтобы справиться с шумом в данных, можно реализовать функцию для удаления флуктуаций ниже заданного порога. Код не отображается, поскольку он выходит за рамки исходного вопроса. Я завернул его в пакет (в основном для автоматизации процесса тестирования) и привожу ниже пример результата:
x_series %>% xtrem::locate_xtrem()
x_series %>% xtrem::locate_xtrem() %>% remove_noise()
Вот решение для минимумов:
@ Решение Бена
x <- c(1,2,3,2,1,2,1)
which(diff(sign(diff(x)))==+2)+1 # 5
Пожалуйста, рассмотрите случаи на посту Томми!
Решение @ Томми:
localMinima <- function(x) {
# Use -Inf instead if x is numeric (non-integer)
y <- diff(c(.Machine$integer.max, x)) > 0L
rle(y)$lengths
y <- cumsum(rle(y)$lengths)
y <- y[seq.int(1L, length(y), 2L)]
if (x[[1]] == x[[2]]) {
y <- y[-1]
}
y
}
x <- c(1,2,9,9,2,1,1,5,5,1)
localMinima(x) # 1, 7, 10
x <- c(2,2,9,9,2,1,1,5,5,1)
localMinima(x) # 7, 10
x <- c(3,2,9,9,2,1,1,5,5,1)
localMinima(x) # 2, 7, 10
Пожалуйста, обратите внимание: ни localMaxima ни localMinima может обрабатывать дублированные максимумы / минимумы при запуске!
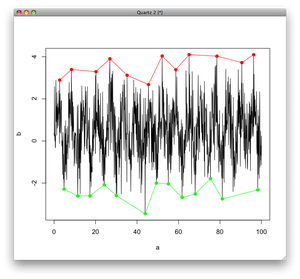
У меня были некоторые проблемы с получением местоположений для работы в предыдущих решениях, и я нашел способ получить минимумы и максимумы напрямую. Приведенный ниже код сделает это и отобразит его, отметив минимумы зеленым цветом и максимумы красным. в отличие от which.max() функция, которая вытянет все индексы минимумов / максимумов из фрейма данных. Нулевое значение добавляется в первом diff() функция для учета отсутствующей уменьшенной длины результата, возникающего при каждом использовании функции. Вставить это в самый внутренний diff() Вызов функции избавляет от необходимости добавлять смещение вне логического выражения. Это не имеет большого значения, но я чувствую, что это более чистый способ сделать это.
# create example data called stockData
stockData = data.frame(x = 1:30, y=rnorm(30,7))
# get the location of the minima/maxima. note the added zero offsets
# the location to get the correct indices
min_indexes = which(diff( sign(diff( c(0,stockData$y)))) == 2)
max_indexes = which(diff( sign(diff( c(0,stockData$y)))) == -2)
# get the actual values where the minima/maxima are located
min_locs = stockData[min_indexes,]
max_locs = stockData[max_indexes,]
# plot the data and mark minima with red and maxima with green
plot(stockData$y, type="l")
points( min_locs, col="red", pch=19, cex=1 )
points( max_locs, col="green", pch=19, cex=1 )
Эта функция Тимоти Пуазо удобна для шумных сериалов:
3 мая 2009 г.
Алгоритм для поиска локальных
экстремумов в векторе. Раздел: Алгоритм - Теги: Экстремумы, Временные ряды - Тимоти Пуазо @ 18:46Я трачу некоторое время на поиск алгоритма для поиска локальных экстремумов в векторе (временном ряду). Решение, которое я использовал, заключается в том, чтобы "пройти" по вектору на шаг больше 1, чтобы сохранить только одно значение, даже если значения очень зашумлены (см. Рисунок в конце сообщения).
Это выглядит так:
findpeaks <- function(vec,bw=1,x.coo=c(1:length(vec)))
{
pos.x.max <- NULL
pos.y.max <- NULL
pos.x.min <- NULL
pos.y.min <- NULL for(i in 1:(length(vec)-1)) { if((i+1+bw)>length(vec)){
sup.stop <- length(vec)}else{sup.stop <- i+1+bw
}
if((i-bw)<1){inf.stop <- 1}else{inf.stop <- i-bw}
subset.sup <- vec[(i+1):sup.stop]
subset.inf <- vec[inf.stop:(i-1)]
is.max <- sum(subset.inf > vec[i]) == 0
is.nomin <- sum(subset.sup > vec[i]) == 0
no.max <- sum(subset.inf > vec[i]) == length(subset.inf)
no.nomin <- sum(subset.sup > vec[i]) == length(subset.sup)
if(is.max & is.nomin){
pos.x.max <- c(pos.x.max,x.coo[i])
pos.y.max <- c(pos.y.max,vec[i])
}
if(no.max & no.nomin){
pos.x.min <- c(pos.x.min,x.coo[i])
pos.y.min <- c(pos.y.min,vec[i])
}
}
return(list(pos.x.max,pos.y.max,pos.x.min,pos.y.min))
}
В pracma пакет, используйте
tt <- c(1,2,3,2,1, 1, 2, 1)
tt_peaks <- findpeaks(tt, zero = "0", peakpat = NULL,
minpeakheight = -Inf, minpeakdistance = 1, threshold = 0, npeaks = 0, sortstr = FALSE)
[,1] [,2] [,3] [,4]
[1,] 3 3 1 5
[2,] 2 7 6 8
Это возвращает матрицу с 4 столбцами. Первый столбец показывает абсолютные значения локальных пиков. 2-й столбец - это индексы. 3-й и 4-й столбцы - это начало и конец пиков (с потенциальным перекрытием).
См. https://www.rdocumentation.org/packages/pracma/versions/1.9.9/topics/findpeaks для получения подробной информации.
Одно предостережение: я использовал его в серии нецелых чисел, и пик был на один индекс слишком поздно (для всех пиков), и я не знаю почему. Поэтому мне пришлось вручную удалить "1" из моего вектора индекса (ничего страшного).
Finding local maxima and minima for a not so easy sequence e.g. 1 0 1 1 2 0 1 1 0 1 1 1 0 1 I would give their positions at (1), 5, 7.5, 11 and (14) for maxima and 2, 6, 9, 13 for minima.
#Position 1 1 1 1 1
# 1 2 3 4 5 6 7 8 9 0 1 2 3 4
x <- c(1,0,1,1,2,0,1,1,0,1,1,1,0,1) #Frequency
# p v p v p v p v p p..Peak, v..Valey
peakPosition <- function(x, inclBorders=TRUE) {
if(inclBorders) {y <- c(min(x), x, min(x))
} else {y <- c(x[1], x)}
y <- data.frame(x=sign(diff(y)), i=1:(length(y)-1))
y <- y[y$x!=0,]
idx <- diff(y$x)<0
(y$i[c(idx,F)] + y$i[c(F,idx)] - 1)/2
}
#Find Peaks
peakPosition(x)
#1.0 5.0 7.5 11.0 14.0
#Find Valeys
peakPosition(-x)
#2 6 9 13
peakPosition(c(1,2,3,2,1,1,2,1)) #3 7
Здесь мы видим много хороших функций и идей с разными функциями. Проблема почти во всех примерах - эффективность. Часто мы видим использование сложных функций, таких как
diff() или же
for()-циклы, которые становятся медленными, когда задействованы большие наборы данных. Позвольте мне представить эффективную функцию, которую я использую каждый день, с минимальным набором функций, но очень быстрой:
Функция локального максимума
amax()
Цель состоит в том, чтобы обнаружить все локальные максимумы в векторе с действительными значениями. Если первый элемент
x[1]является глобальным максимумом, он игнорируется, потому что нет информации о предыдущем элементе. Если есть плато, определяется первый край.
@param x числовой вектор
@return возвращает признаки локальных максимумов. Если
x[1] = max, то игнорируется.
amax <- function(x)
{
a1 <- c(0,x,0)
a2 <- c(x,0,0)
a3 <- c(0,0,x)
e <- which((a1 >= a2 & a1 > a3)[2:(length(x))])
if(!is.na(e[1] == 1))
if(e[1]==1)
e <- e[-1]
if(length(e) == 0) e <- NaN
return (e)
}
a <- c(1,2,3,2,1,5,5,4)
amax(a) # 3, 6
Мне понравилось решение @mikeck, так что мне не пришлось преобразовывать свои кадры данных туда и обратно из объекта зоопарка. Но я также хотел использовать окно шире 1. Их решение рассматривает только значение x вдали от интересующего значения, а не значения в пределах расстояния x. Вот что я придумал. Вам нужно будет добавить дополнительную линию отставания/опережения для каждого значения, отличного от интересующего вас значения, которое вы хотите посмотреть.
x <- data.frame(AIC = c(98, 97, 96, 97, 98, 99, 98, 98, 97, 96, 95, 94, 93, 92, 93, 94, 95, 96, 95, 94, 93, 92, 91, 90, 89, 88))
x <- x %>%
mutate(local.minima = if_else(lag(AIC) > AIC & lead(AIC) > AIC &
lag(AIC, 2) > AIC & lead(AIC, 2) > AIC &
lag(AIC, 3) > AIC & lead(AIC, 3) > AIC, TRUE, FALSE),
local.minima = if_else(is.na(local.minima), TRUE, local.minima))
Я опубликовал это в другом месте, но я думаю, что это интересный способ сделать это. Я не уверен, какова его вычислительная эффективность, но это очень лаконичный способ решения проблемы.
vals=rbinom(1000,20,0.5)
text=paste0(substr(format(diff(vals),scientific=TRUE),1,1),collapse="")
sort(na.omit(c(gregexpr('[ ]-',text)[[1]]+1,ifelse(grepl('^-',text),1,NA),
ifelse(grepl('[^-]$',text),length(vals),NA))))
Улучшение (быстрый и простой метод) формулы, предложенной @BEN и относящейся к случаям, предложенным @TOMMY:
следующая рекурсивная формула обрабатывает любые случаи:
dx=c(0,sign(diff(x)))
numberofzeros= length(dx) - sum(abs(dx)) -1 # to find the number of zeros
# in the dx minus the first one
# which is added intentionally.
#running recursive formula to clear middle zeros
# iterate for the number of zeros
for (i in 1:numberofzeros){
dx = sign(2*dx + c(0,rev(sign(diff(rev(dx))))))
}
Теперь формулу, предоставленную @Ben Bolker, можно использовать с небольшими изменениями:
plot(x)
points(which(diff(dx)==2),x[which(diff(dx)==2)],col = 'blue')#Local MIN.
points(which(diff(dx)==-2),x[which(diff(dx)==-2)],col = 'red')#Local MAX.