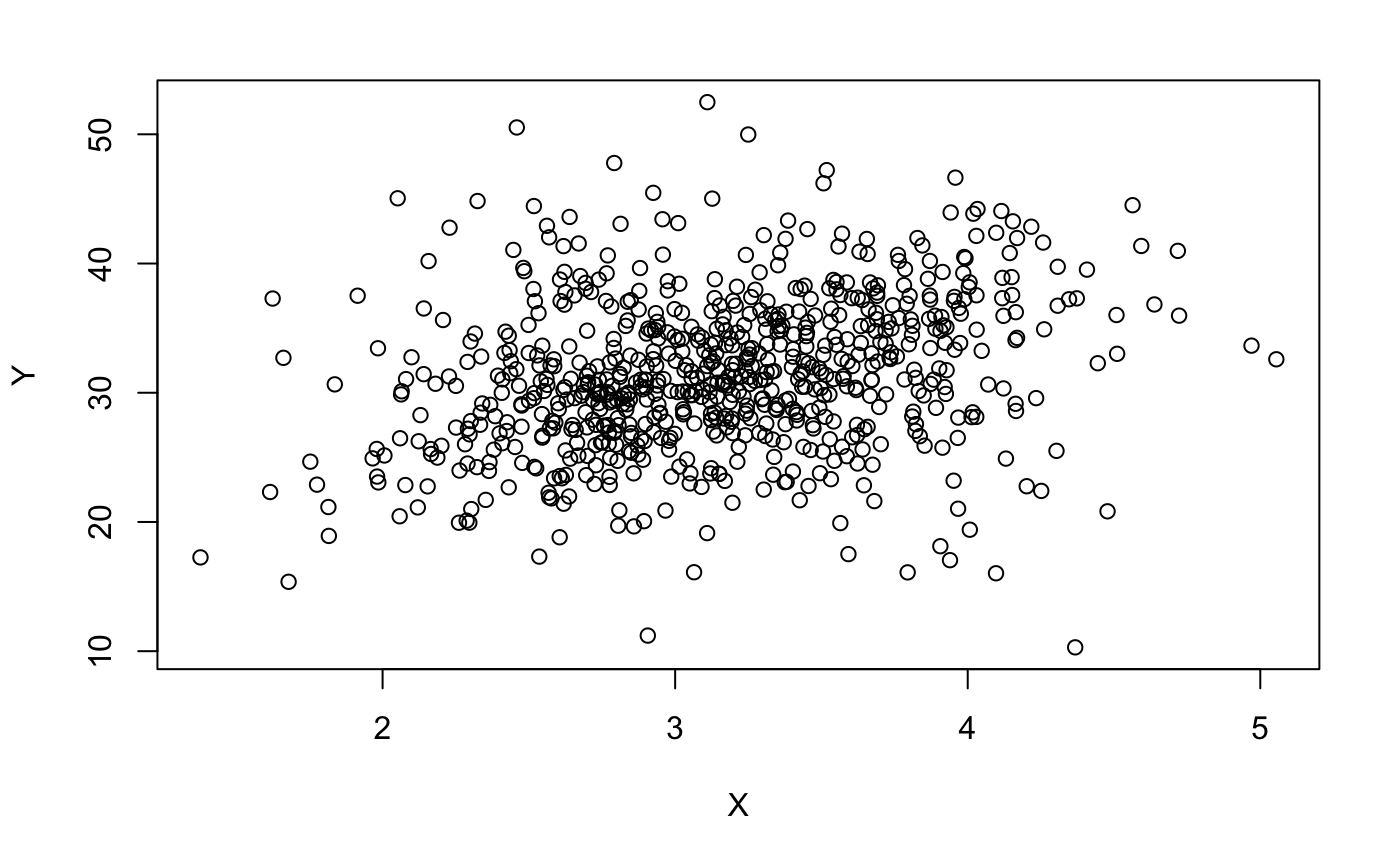
Генерация коррелированных векторов (X,Y), в результате чего rho = f(x) "хоккейная клюшка"

Question

Я хочу смоделировать зависимые (с изменением корреляции rho) переменные, чтобы "воспроизвести" эту фигуру.

Точка останова корреляции
rho = 0 для X=x <= 2,4
rho = 0,5 для X=x > 2,4

Двустороннее распределение Y | X
X = N ~ (mu_x, sd_x)
Y | X = N ~ (mu_x + sd_x / sd_y * rho (Y-mu_y), (1-rho ^ 2) sd_x)

Даны:
mu_x = 3,13; sd_x = 0,6
среднее_y = 31,3; sd_y = 6,7

Мой код работает для генерации коррелированных данных, 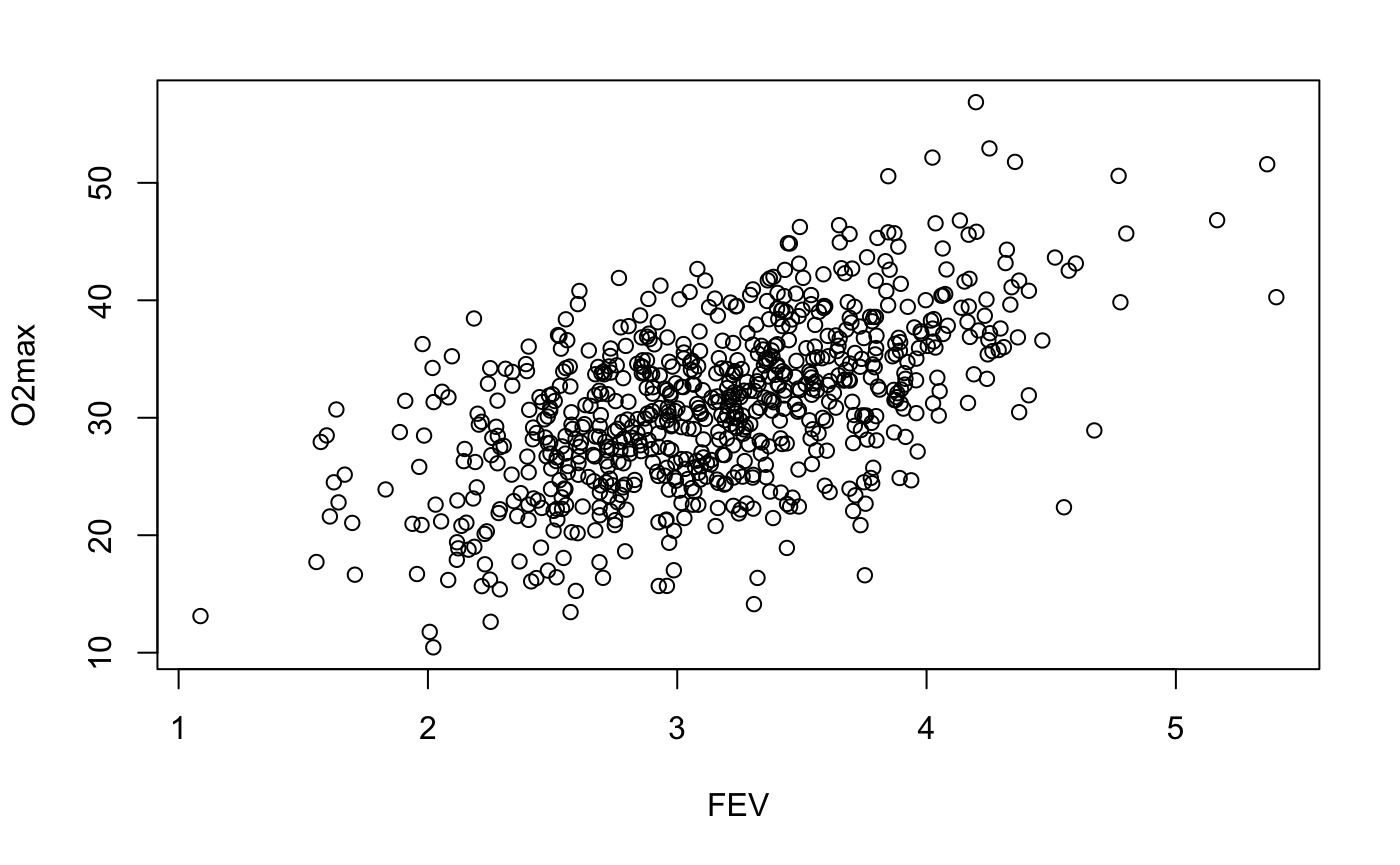но пропускает "точку останова". Вот мой код для сюжета выше:

X = rnorm (n, mean_x, sd_x)
Y = rnorm (n, mean_y + sd_y / sd_x * rho * (X-mean_x), (1-rho ^ 2) * sd_y)

Как мне сделать rho = f(x)? На данный момент я склеиваю два распределения, чтобы получить хоккейную клюшку, похожую на блок разброса.

 # Correlated Vectors (X, Y) - Hockey Stick 
 set.seed = 47
 n = 729
 mean_x = 3.13; sd_x = 0.6  # FEV
 mean_y =  31.3; sd_y = 6.7 # O2max

 # rho and breakpoint
 rho = 0.7; breakpoint = 3.5
 index_break = sum(X<breakpoint)

 # Generate X distributuion
 X = rnorm(n, mean_x, sd_x)

 # Generate Y disrtribution parts
 Y_rho = vector(); Y = vector()
 Y_rho = rnorm(n, mean_y + sd_y/sd_x*rho*(X-mean_x), (1-rho^2)*sd_y[1:index_break]
 Y = rnorm(n, mean_y, sd_y)[(index_break+1):length(FEV)]
 Y = c(Y_rho, Y)

 # plot
 plot(X, Y)

Большое спасибо заранее.