Случайные числа, которые добавляют к 100: Matlab
[Я делю численность населения на разные матрицы и хочу проверить свой код, используя случайные числа на данный момент.]
Быстрый вопрос, ребята, и спасибо за вашу помощь заранее -
Если я использую;
100*rand(9,1)
Каков наилучший способ заставить эти 9 чисел добавить к 100?
Я хотел бы 9 случайных чисел от 0 до 100, которые складываются до 100.
Есть ли встроенная команда, которая делает это, потому что я не могу найти ее.
4 ответа
Я часто вижу ошибку: предположение, что для генерации случайных чисел с заданной суммой нужно просто использовать равномерный случайный набор и просто масштабировать их. Но действительно ли результат действительно случайно, если вы делаете это таким образом?
Попробуйте этот простой тест в двух измерениях. Создайте огромную случайную выборку, затем масштабируйте их до суммы 1. Я буду использовать bsxfun для масштабирования.
xy = rand(10000000,2);
xy = bsxfun(@times,xy,1./sum(xy,2));
hist(xy(:,1),100)
Если бы они были действительно равномерно случайными, то координата x была бы равномерной, как и координата y. Любая ценность будет в равной степени вероятна. Фактически, чтобы две точки суммировали с 1, они должны лежать вдоль линии, соединяющей две точки (0,1), (1,0) в плоскости (x,y). Чтобы точки были одинаковыми, любая точка вдоль этой линии должна быть одинаково вероятной.
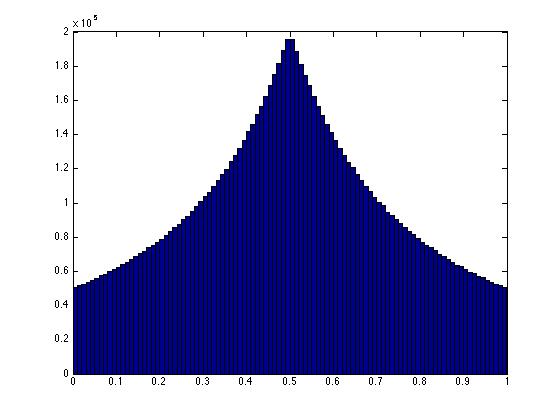
Очевидно, что однородность не работает, когда я использую решение для масштабирования. Любая точка на этой линии НЕ одинаково вероятна. Мы можем видеть, что то же самое происходит в 3-х измерениях. Обратите внимание, что на 3-м рисунке здесь точки в центре треугольной области более плотно упакованы. Это отражение неоднородности.
xyz = rand(10000,3);
xyz = bsxfun(@times,xyz,1./sum(xyz,2));
plot3(xyz(:,1),xyz(:,2),xyz(:,3),'.')
view(70,35)
box on
grid on
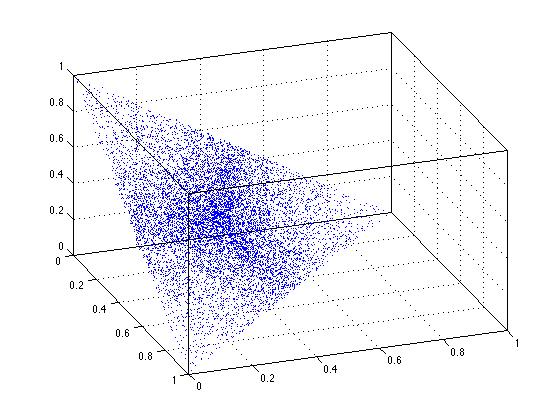
Опять же, простое решение масштабирования не удается. Он просто НЕ дает действительно единообразных результатов в интересующей области.
Можем ли мы сделать лучше? Ну да. Простое решение в 2-й состоит в том, чтобы сгенерировать одно случайное число, которое обозначает расстояние вдоль линии, соединяющей точки (0,1) и 1,0).
t = rand(10000000,1);
xy = t*[0 1] + (1-t)*[1 0];
hist(xy(:,1),100)
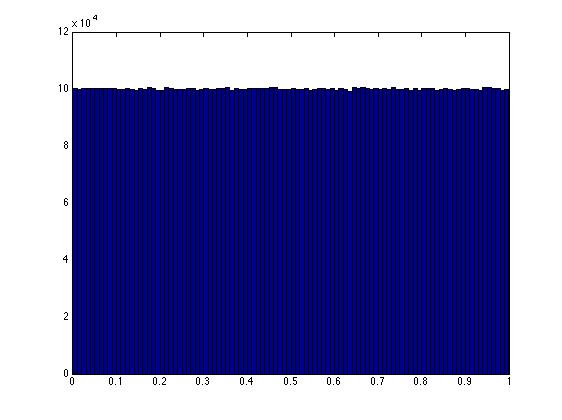
Можно показать, что ЛЮБАЯ точка вдоль линии, определяемой уравнением x+y = 1 в единичном квадрате, теперь с равной вероятностью была выбрана. Это отражено в красивой плоской гистограмме.
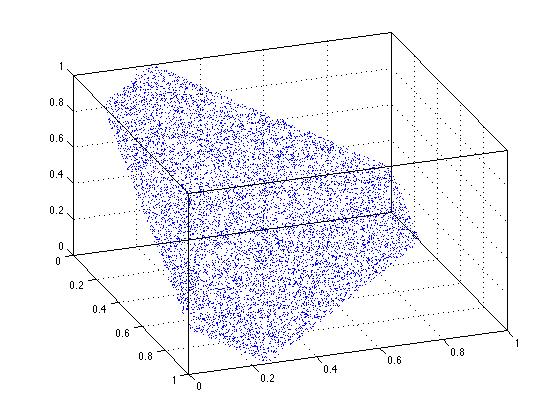
Работает ли уловка сортировки, предложенная Дэвидом Шварцем, в n-измерениях? Ясно, что это происходит в 2-х измерениях, и рисунок ниже показывает, что это происходит в 3-х измерениях. Не вдаваясь в глубокие размышления по этому вопросу, я считаю, что это сработает для рассматриваемого основного случая в n-измерениях.
n = 10000;
uv = [zeros(n,1),sort(rand(n,2),2),ones(n,1)];
xyz = diff(uv,[],2);
plot3(xyz(:,1),xyz(:,2),xyz(:,3),'.')
box on
grid on
view(70,35)
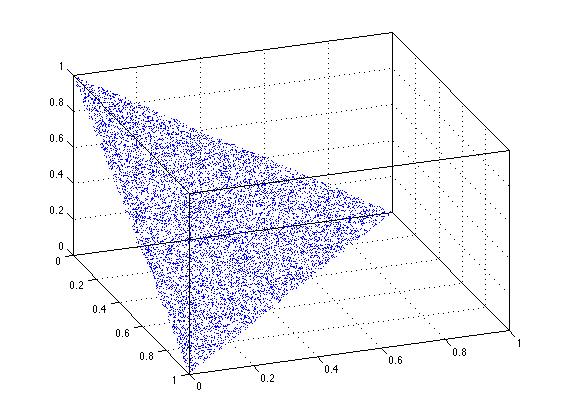
Можно также загрузить функцию randfixedsum из обмена файлами, вклад Роджера Стаффорда. Это более общее решение для генерации действительно однородных случайных множеств в единичном гиперкубе с любой заданной фиксированной суммой. Таким образом, для генерации случайных наборов точек, лежащих в единичном 3-кубе, при условии ограничения они составляют 1,25...
xyz = randfixedsum(3,10000,1.25,0,1)';
plot3(xyz(:,1),xyz(:,2),xyz(:,3),'.')
view(70,35)
box on
grid on
Один простой способ - выбрать 8 случайных чисел от 0 до 100. Добавьте 0 и 100 в список, чтобы получить 10 чисел. Сортировать их. Затем выведите разницу между каждой последовательной парой чисел. Например, вот 8 случайных чисел от 0 до 100:
96, 38, 95, 5, 13, 57, 13, 20
Так что добавьте 0 и 100 и сортируйте.
0, 5, 13, 13, 20, 38, 57, 95, 96, 100
Теперь вычтите:
5-0 = 5
13-5 = 8
13-13 = 0
20-13 = 7
38-20 = 18
57-38 = 19
95-57 = 38
96-95 = 1
100-96 = 4
И вот, у вас есть это, девять чисел, которые составляют 100: 0, 1, 4, 5, 7, 8, 18, 19, 38. То, что я получил ноль, а одно было просто странной удачей.
Еще не поздно дать правильный ответ
Давайте поговорим о выборке X1...XN в диапазоне [0...1], такой, что Sum(X1, ..., XN) равен 1. Тогда вы можете изменить его масштаб до 100
Это называется распространением Дирихле, и ниже приведен пример кода. Простейший случай, когда все параметры равны 1, тогда все предельные распределения для X1,..., XN будут U(0,1). В общем случае, если параметры отличаются от 1, предельные распределения могут иметь пики.
----------------- взято отсюда ---------------------
Дирихле является вектором гамма-случайных переменных единичного масштаба, нормированных по их сумме. Таким образом, без проверки ошибок, вы получите следующее:
a = [1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0 1.0]; // 9 numbers to sample
n = 10000;
r = drchrnd(a,n)
function r = drchrnd(a,n)
p = length(a);
r = gamrnd(repmat(a,n,1),1,n,p);
r = r ./ repmat(sum(r,2),1,p);
Возьмите список из N - 1 чисел, создайте список из N + 1 чисел, вставив 0 и 100, отсортируйте список и разведите их до общего числа N чисел.