Выбор рулетки в генетических алгоритмах
Кто-нибудь может предоставить какой-нибудь псевдокод для функции выбора рулетки? Как бы я это реализовал:
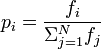
Я не очень понимаю, как читать эту математическую запись. Я никогда не принимал никакой вероятности или статистики.
13 ответов
Прошло несколько лет с тех пор, как я сделал это сам, однако следующий псевдокод был найден достаточно легко в Google.
для всех жителей
сумма += пригодность этого человека
конец для
для всех жителей
вероятность = сумма вероятностей + (пригодность / сумма)
сумма вероятностей += вероятность
конец для
цикл, пока новое население не заполнится
сделай это дважды
число = случайное число от 0 до 1
для всех жителей
если число> вероятность, но меньше, чем следующая вероятность
тогда вы были выбраны
конец для
конец
создать потомство
конец циклаСайт, откуда это пришло, можно найти здесь, если вам нужна дополнительная информация.
Уже много правильных решений, но я думаю, что этот код более понятен.
def select(fs):
p = random.uniform(0, sum(fs))
for i, f in enumerate(fs):
if p <= 0:
break
p -= f
return i
Кроме того, если вы накапливаете фс, вы можете найти более эффективное решение.
cfs = [sum(fs[:i+1]) for i in xrange(len(fs))]
def select(cfs):
return bisect.bisect_left(cfs, random.uniform(0, cfs[-1]))
Это и быстрее, и это очень лаконичный код. STL в C++ имеет похожий алгоритм деления пополам, если вы используете этот язык.
Опубликованный псевдокод содержал некоторые неясные элементы, и он добавляет сложность генерации потомства вместо выполнения чистого отбора. Вот простая реализация этого псевдокода на python:
def roulette_select(population, fitnesses, num):
""" Roulette selection, implemented according to:
<http://stackru.com/questions/177271/roulette
-selection-in-genetic-algorithms/177278#177278>
"""
total_fitness = float(sum(fitnesses))
rel_fitness = [f/total_fitness for f in fitnesses]
# Generate probability intervals for each individual
probs = [sum(rel_fitness[:i+1]) for i in range(len(rel_fitness))]
# Draw new population
new_population = []
for n in xrange(num):
r = rand()
for (i, individual) in enumerate(population):
if r <= probs[i]:
new_population.append(individual)
break
return new_population
Это называется выбором колеса рулетки посредством стохастического принятия:
/// \param[in] f_max maximum fitness of the population
///
/// \return index of the selected individual
///
/// \note Assuming positive fitness. Greater is better.
unsigned rw_selection(double f_max)
{
for (;;)
{
// Select randomly one of the individuals
unsigned i(random_individual());
// The selection is accepted with probability fitness(i) / f_max
if (uniform_random_01() < fitness(i) / f_max)
return i;
}
}
Среднее количество попыток, необходимых для одного выбора:
τ = fmax / avg (f)
- fmax - максимальная приспособленность населения
- avg (f) - средняя пригодность
τ явно не зависит от количества особей в популяции (N), но соотношение может изменяться в зависимости от N.
Однако во многих приложениях (где пригодность остается ограниченной и средняя пригодность не уменьшается до 0 для увеличения N) τ не увеличивается неограниченно с N, и, таким образом, типичная сложность этого алгоритма составляет O (1) (выбор колеса рулетки с использованием Алгоритмы поиска имеют сложность O (N) или O (log N)).
Распределение вероятностей этой процедуры действительно такое же, как при классическом выборе колеса рулетки.
Для получения дополнительной информации см.:
- Выбор колеса рулетки посредством стохастического принятия (Адам Липоски, Дорота Липовска - 2011)
Вот некоторый код в C:
// Find the sum of fitnesses. The function fitness(i) should
//return the fitness value for member i**
float sumFitness = 0.0f;
for (int i=0; i < nmembers; i++)
sumFitness += fitness(i);
// Get a floating point number in the interval 0.0 ... sumFitness**
float randomNumber = (float(rand() % 10000) / 9999.0f) * sumFitness;
// Translate this number to the corresponding member**
int memberID=0;
float partialSum=0.0f;
while (randomNumber > partialSum)
{
partialSum += fitness(memberID);
memberID++;
}
**// We have just found the member of the population using the roulette algorithm**
**// It is stored in the "memberID" variable**
**// Repeat this procedure as many times to find random members of the population**
Из вышеприведенного ответа я получил следующее, что было для меня понятнее, чем сам ответ.
Чтобы привести пример:
Random (sum):: Random (12) Итерируя по совокупности, мы проверяем следующее: random Давайте выберем 7 в качестве случайного числа. В этом примере наиболее подходящий (индекс 3) имеет самый высокий процент выбора (33%); так как случайное число должно приземлиться только в пределах 6->10, и оно будет выбрано.Index | Fitness | Sum | 7 < Sum
0 | 2 | 2 | false
1 | 3 | 5 | false
2 | 1 | 6 | false
3 | 4 | 10 | true
4 | 2 | 12 | ...
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
}
double rand = (((double)rand() / (double)RAND_MAX) * sum);
sum = 0;
for (unsigned int i=0;i<sets.size();i++) {
sum += sets[i].eval();
if (rand < sum) {
//breed i
break;
}
}
Профессор Трун из Стэнфордской лаборатории искусственного интеллекта также представил быстрый (er?) Код повторной выборки в python во время своего CS373 Udacity. Результат поиска Google привел к следующей ссылке:
http://www.udacity-forums.com/cs373/questions/20194/fast-resampling-algorithm
Надеюсь это поможет
Вот компактная реализация Java, которую я недавно написал для выбора рулетки, надеюсь, полезной.
public static gene rouletteSelection()
{
float totalScore = 0;
float runningScore = 0;
for (gene g : genes)
{
totalScore += g.score;
}
float rnd = (float) (Math.random() * totalScore);
for (gene g : genes)
{
if ( rnd>=runningScore &&
rnd<=runningScore+g.score)
{
return g;
}
runningScore+=g.score;
}
return null;
}
Выбор колеса рулетки в MatLab:
TotalFitness=sum(Fitness);
ProbSelection=zeros(PopLength,1);
CumProb=zeros(PopLength,1);
for i=1:PopLength
ProbSelection(i)=Fitness(i)/TotalFitness;
if i==1
CumProb(i)=ProbSelection(i);
else
CumProb(i)=CumProb(i-1)+ProbSelection(i);
end
end
SelectInd=rand(PopLength,1);
for i=1:PopLength
flag=0;
for j=1:PopLength
if(CumProb(j)<SelectInd(i) && CumProb(j+1)>=SelectInd(i))
SelectedPop(i,1:IndLength)=CurrentPop(j+1,1:IndLength);
flag=1;
break;
end
end
if(flag==0)
SelectedPop(i,1:IndLength)=CurrentPop(1,1:IndLength);
end
end
Итак, есть 2 способа реализации выбора колеса рулетки: обычный и стохастический прием.
Обычный алгоритм:
# there will be some amount of repeating organisms here.
mating_pool = []
all_organisms_in_population.each do |organism|
organism.fitness.times { mating_pool.push(organism) }
end
# [very_fit_organism, very_fit_organism, very_fit_organism, not_so_fit_organism]
return mating_pool.sample #=> random, likely fit, parent!
Алгоритмстохастического принятия:
max_fitness_in_population = all_organisms_in_population.sort_by(:fitness)[0]
loop do
random_parent = all_organisms_in_population.sample
probability = random_parent.fitness/max_fitness_in_population * 100
# if random_parent's fitness is 90%,
# it's very likely that rand(100) is smaller than it.
if rand(100) < probability
return random_parent #=> random, likely fit, parent!
else
next #=> or let's keep on searching for one.
end
end
Вы можете выбрать любой, они будут возвращать идентичные результаты.
Полезные ресурсы:
http://natureofcode.com/book/chapter-9-the-evolution-of-code - понятная для новичков глава о генетических алгоритмах. объясняет выбор колеса рулетки как набор деревянных букв (чем больше вы вставляете - тем больше шансов выбрать обычный алгоритм A).
https://en.wikipedia.org/wiki/Fitness_proportionate_selection - описывает алгоритм стохастического принятия.
Вот код на Python. Этот код также может обрабатывать отрицательное значение пригодности.
from numpy import min, sum, ptp, array
from numpy.random import uniform
list_fitness1 = array([-12, -45, 0, 72.1, -32.3])
list_fitness2 = array([0.5, 6.32, 988.2, 1.23])
def get_index_roulette_wheel_selection(list_fitness=None):
""" It can handle negative also. Make sure your list fitness is 1D-numpy array"""
scaled_fitness = (list_fitness - min(list_fitness)) / ptp(list_fitness)
minimized_fitness = 1.0 - scaled_fitness
total_sum = sum(minimized_fitness)
r = uniform(low=0, high=total_sum)
for idx, f in enumerate(minimized_fitness):
r = r + f
if r > total_sum:
return idx
get_index_roulette_wheel_selection(list_fitness1)
get_index_roulette_wheel_selection(list_fitness2)
- Убедитесь, что ваш фитнес-список представляет собой массив 1D-numpy
- Список пригодности увеличен до диапазона [0, 1]
- Преобразование максимальной задачи в минимальную задачу на 1.0 - scaled_fitness_list
- Случайное число от 0 до суммы (minimizzed_fitness_list)
- Продолжайте добавлять элемент в свернутый список пригодности, пока мы не получим значение больше общей суммы
- Вы можете увидеть, если фитнес маленький -> он имеет большее значение в minimized_fitness -> У него больше шансов добавить и сделать значение больше, чем общая сумма.
Based on my research ,Here is another implementation in C# if there is a need for it:
//those with higher fitness get selected wit a large probability
//return-->individuals with highest fitness
private int RouletteSelection()
{
double randomFitness = m_random.NextDouble() * m_totalFitness;
int idx = -1;
int mid;
int first = 0;
int last = m_populationSize -1;
mid = (last - first)/2;
// ArrayList's BinarySearch is for exact values only
// so do this by hand.
while (idx == -1 && first <= last)
{
if (randomFitness < (double)m_fitnessTable[mid])
{
last = mid;
}
else if (randomFitness > (double)m_fitnessTable[mid])
{
first = mid;
}
mid = (first + last)/2;
// lies between i and i+1
if ((last - first) == 1)
idx = last;
}
return idx;
}
Это расширение массива Swift 4 реализует взвешенный случайный отбор, также известный как выбор рулетки из его элементов:
public extension Array where Element == Double {
/// Consider the elements as weight values and return a weighted random selection by index.
/// a.k.a Roulette wheel selection.
func weightedRandomIndex() -> Int {
var selected: Int = 0
var total: Double = self[0]
for i in 1..<self.count { // start at 1
total += self[i]
if( Double.random(in: 0...1) <= (self[i] / total)) { selected = i }
}
return selected
}
}
Например, дан массив из двух элементов:
[0.9, 0.1]
weightedRandomIndex() вернет ноль 90% времени и один 10% времени.
Вот более полный тест:
let weights = [0.1, 0.7, 0.1, 0.1]
var results = [Int:Int]()
let n = 100000
for _ in 0..<n {
let index = weights.weightedRandomIndex()
results[index] = results[index, default:0] + 1
}
for (key,val) in results.sorted(by: { a,b in weights[a.key] < weights[b.key] }) {
print(weights[key], Double(val)/Double(n))
}
выход:
0.1 0.09906
0.1 0.10126
0.1 0.09876
0.7 0.70092
Этот ответ в основном совпадает с ответом Эндрю Мао здесь: /questions/41498123/algoritm-vyibora-kolesa-ruletki/41498147#41498147
Я написал версию на C# и действительно ищу подтверждение того, что это действительно правильно:
(roulette_selector - это случайное число, которое будет в диапазоне от 0,0 до 1,0)
private Individual Select_Roulette(double sum_fitness)
{
Individual ret = new Individual();
bool loop = true;
while (loop)
{
//this will give us a double within the range 0.0 to total fitness
double slice = roulette_selector.NextDouble() * sum_fitness;
double curFitness = 0.0;
foreach (Individual ind in _generation)
{
curFitness += ind.Fitness;
if (curFitness >= slice)
{
loop = false;
ret = ind;
break;
}
}
}
return ret;
}