Как происходит "переполнение стека" и как его предотвратить?
Как происходит переполнение стека и каков наилучший способ предотвратить это, или способы его предотвращения, особенно на веб-серверах, но другие примеры также будут интересны?
11 ответов
стек
В этом контексте стек является последним входным, первым выходным буфером, в который вы помещаете данные во время работы вашей программы. "Последний пришел, первый вышел" (LIFO) означает, что последнее, что вы вставляете, это всегда первое, что вы возвращаете - если вы помещаете 2 стека в стек, "А", а затем "В", то первое, что вы вставляете со стека будет "B", а следующая вещь - "A".
Когда вы вызываете функцию в своем коде, следующая инструкция после вызова функции сохраняется в стеке и в любом пространстве памяти, которое может быть перезаписано вызовом функции. Вызываемая функция может использовать больше стека для своих локальных переменных. Когда это сделано, он освобождает используемое пространство стека локальной переменной, а затем возвращается к предыдущей функции.
Переполнение стека
Переполнение стека - это когда вы используете больше памяти для стека, чем предполагалось использовать вашей программе. Во встроенных системах у вас может быть только 256 байтов для стека, и если каждая функция занимает 32 байта, то вы можете иметь только вызовы функций 8: глубокая функция 1 вызывает функцию 2, которая вызывает функцию 3, которая вызывает функцию 4 .... кто вызывает функция 8, которая вызывает функцию 9, но функция 9 перезаписывает память вне стека. Это может перезаписать память, код и т. Д.
Многие программисты совершают эту ошибку, вызывая функцию A, которая затем вызывает функцию B, которая затем вызывает функцию C, которая затем вызывает функцию A. Это может работать большую часть времени, но только один неправильный ввод приведет к тому, что он навсегда войдет в этот круг пока компьютер не распознает, что стек перегружен.
Причиной этого также являются рекурсивные функции, но если вы пишете рекурсивно (т. Е. Ваша функция вызывает себя), вам нужно знать об этом и использовать статические / глобальные переменные для предотвращения бесконечной рекурсии.
Как правило, ОС и используемый вами язык программирования управляют стеком, и это не в ваших руках. Вы должны взглянуть на свой график вызовов (древовидную структуру, которая показывает от вашей основной функции, которую вызывает каждая функция), чтобы увидеть, насколько глубоки ваши вызовы функций, и обнаружить циклы и рекурсию, которые не предназначены. Преднамеренные циклы и рекурсия должны быть искусственно проверены на наличие ошибок, если они вызывают друг друга слишком много раз.
Помимо хороших практик программирования, статического и динамического тестирования, в этих системах высокого уровня мало что можно сделать.
Встроенные системы
Во встроенном мире, особенно в коде высокой надежности (автомобильный, авиационный, космический), вы проводите подробные обзоры и проверки кода, но также делаете следующее:
- Запретить рекурсию и циклы - обеспечивается политикой и тестированием
- Держите код и стеки далеко друг от друга (код во флэш-памяти, стек в оперативной памяти, и никогда не встречаться)
- Поместите защитные полосы вокруг стека - пустую область памяти, которую вы заполняете магическим числом (обычно это программная команда прерывания, но здесь много вариантов), и сотни или тысячи раз в секунду вы смотрите на защитные полосы, чтобы убедиться, они не были перезаписаны.
- Используйте защиту памяти (т. Е. Не выполняйте в стеке, не читайте и не записывайте только вне стека)
- Прерывания не вызывают вторичные функции - они устанавливают флаги, копируют данные и позволяют приложению позаботиться об их обработке (в противном случае вы можете получить 8 в глубине дерева вызовов функций, иметь прерывание, а затем выйти из других функций внутри прерывать, вызывая выброс). У вас есть несколько деревьев вызовов - одно для основных процессов и одно для каждого прерывания. Если ваши прерывания могут прервать друг друга... ну, есть драконы...
Языки и системы высокого уровня
Но на языках высокого уровня работают в операционных системах:
- Сократите хранилище локальных переменных (локальные переменные хранятся в стеке - хотя компиляторы достаточно умны в этом и иногда помещают большие локальные ресурсы в кучу, если дерево вызовов мелкое)
- Избегайте или строго ограничивайте рекурсию
- Не разбивайте свои программы слишком далеко на меньшие и меньшие функции - даже без учета локальных переменных каждый вызов функции занимает до 64 байт в стеке (32-битный процессор, сохраняя половину регистров ЦП, флагов и т. Д.)
- Держите дерево вызовов мелким (аналогично приведенному выше утверждению)
Веб-серверы
Это зависит от имеющейся у вас "песочницы", можете ли вы контролировать или даже видеть стек. Скорее всего, вы можете обращаться с веб-серверами так же, как с любым другим языком и операционной системой высокого уровня - это в значительной степени не в ваших руках, но проверьте язык и стек серверов, которые вы используете. Например, можно создать стек на вашем сервере SQL.
-Адам
Переполнение стека в реальном коде происходит очень редко. Большинство ситуаций, в которых это происходит, являются рекурсиями, когда завершение было забыто. Однако это может происходить редко в структурах с высокой степенью вложенности, например, в больших документах XML Единственная реальная помощь здесь - это рефакторинг кода для использования явного стекового объекта вместо стека вызовов.
Большинство людей скажут вам, что переполнение стека происходит с рекурсией без пути выхода - хотя в большинстве случаев это так, если вы работаете с достаточно большими структурами данных, даже правильный путь выхода из рекурсии вам не поможет.
Некоторые варианты в этом случае:
- Поиск в ширину
- Хвостовая рекурсия, отличная запись в блоге.Net (извините, 32-разрядная версия.Net)
Переполнение стека происходит, когда Джефф и Джоэл хотят дать миру лучшее место, чтобы получить ответы на технические вопросы. Слишком поздно предотвращать переполнение стека. Этот "другой сайт" мог бы предотвратить это, не будучи лохматым.;)
Бесконечная рекурсия является распространенным способом получения ошибки переполнения стека. Чтобы предотвратить - всегда убедитесь, что есть выходной путь, который будет выбран.:-)
Другой способ получить переполнение стека (по крайней мере в C/C++) - объявить в стеке какую-то огромную переменную.
char hugeArray[100000000];
Это сделает это.
Помимо формы переполнения стека, получаемой при прямой рекурсии (например, Fibonacci(1000000)), более тонкой его формой, которую я испытывал много раз, является косвенная рекурсия, когда функция вызывает другую функцию, которая вызывает другую, а затем одна из этих функций снова вызывает первую.
Обычно это может происходить в функциях, которые вызываются в ответ на события, но сами могут генерировать новые события, например:
void WindowSizeChanged(Size& newsize) {
// override window size to constrain width
newSize.width=200;
ResizeWindow(newSize);
}
В этом случае вызов ResizeWindow может вызвать WindowSizeChanged() обратный вызов, который будет запущен снова, который вызывает ResizeWindow снова, пока вы не исчерпаете стек. В подобных ситуациях вам часто приходится откладывать ответ на событие до тех пор, пока не вернется фрейм стека, например, отправив сообщение.
Обычно переполнение стека является результатом бесконечного рекурсивного вызова (учитывая обычный объем памяти в стандартных компьютерах в настоящее время).
Когда вы совершаете вызов метода, функции или процедуры, "стандартный" способ или выполнение вызова состоит из:
- Перенос направления возврата для вызова в стек (это следующее предложение после вызова)
- Обычно пространство для возвращаемого значения зарезервировано в стеке
- Загрузка каждого параметра в стек (порядок расходится и зависит от каждого компилятора, также некоторые из них иногда сохраняются в регистрах ЦП для повышения производительности)
- Делая фактический звонок.
Таким образом, обычно это занимает несколько байтов в зависимости от количества и типа параметров, а также от архитектуры машины.
Тогда вы увидите, что если вы начнете делать рекурсивные вызовы, стек начнет расти. Теперь стек обычно зарезервирован в памяти таким образом, что он растет в направлении, противоположном куче, поэтому при большом количестве вызовов без "возврата" стек начинает заполняться.
Теперь в старые времена переполнение стека могло происходить просто потому, что вы исчерпали всю доступную память, вот так. С моделью виртуальной памяти (до 4 ГБ в системе X86), которая обычно выходит за рамки, если вы получаете ошибку переполнения стека, ищите бесконечный рекурсивный вызов.
Я воссоздал проблему переполнения стека, получив наиболее распространенное число Фибоначчи, то есть 1, 1, 2, 3, 5... так что расчет для fib(1) = 1 или fib(3) = 2.. fib(n знак равно
для n, скажем, нас будет интересовать - что, если n = 100000, то каким будет соответствующее число Фибоначчи??
Подход с одним циклом, как показано ниже -
package com.company.dynamicProgramming;
import java.math.BigInteger;
public class FibonacciByBigDecimal {
public static void main(String ...args) {
int n = 100000;
BigInteger[] fibOfnS = new BigInteger[n + 1];
System.out.println("fibonacci of "+ n + " is : " + fibByLoop(n));
}
static BigInteger fibByLoop(int n){
if(n==1 || n==2 ){
return BigInteger.ONE;
}
BigInteger fib = BigInteger.ONE;
BigInteger fip = BigInteger.ONE;
for (int i = 3; i <= n; i++){
BigInteger p = fib;
fib = fib.add(fip);
fip = p;
}
return fib;
}
}
это довольно просто, и результат -
fibonacci of 100000 is : 2597406934722172416615503402127591541488048538651769658472477070395253454351127368626555677283671674475463758722307443211163839947387509103096569738218830449305228763853133492135302679278956701051276578271635608073050532200243233114383986516137827238124777453778337299916214634050054669860390862750996639366409211890125271960172105060300350586894028558103675117658251368377438684936413457338834365158775425371912410500332195991330062204363035213756525421823998690848556374080179251761629391754963458558616300762819916081109836526352995440694284206571046044903805647136346033000520852277707554446794723709030979019014860432846819857961015951001850608264919234587313399150133919932363102301864172536477136266475080133982431231703431452964181790051187957316766834979901682011849907756686456845066287392485603914047605199550066288826345877189410680370091879365001733011710028310473947456256091444932821374855573864080579813028266640270354294412104919995803131876805899186513425175959911520563155337703996941035518275274919959802257507902037798103089922984996304496255814045517000250299764322193462165366210841876745428298261398234478366581588040819003307382939500082132009374715485131027220817305432264866949630987914714362925554252624043999615326979876807510646819068792118299167964409178271868561702918102212679267401362650499784968843680975254700131004574186406448299485872551744746695651879126916993244564817673322257149314967763345846623830333820239702436859478287641875788572910710133700300094229333597292779191409212804901545976262791057055248158884051779418192905216769576608748815567860128818354354292307397810154785701328438612728620176653953444993001980062953893698550072328665131718113588661353747268458543254898113717660519461693791688442534259478126310388952047956594380715301911253964847112638900713362856910155145342332944128435722099628674611942095166100230974070996553190050815866991144544264788287264284501725332048648319457892039984893823636745618220375097348566847433887249049337031633826571760729778891798913667325190623247118037280173921572390822769228077292456662750538337500692607721059361942126892030256744356537800831830637593334502350256972906515285327194367756015666039916404882563967693079290502951488693413799125174856667074717514938979038653338139534684837808612673755438382110844897653836848318258836339917310455850905663846202501463131183108742907729262215943020429159474030610183981685506695026197376150857176119947587572212987205312060791864980361596092339594104118635168854883911918517906151156275293615849000872150192226511785315089251027528045151238603792184692121533829287136924321527332714157478829590260157195485316444794546750285840236000238344790520345108033282013803880708980734832620122795263360677366987578332625485944906021917368867786241120562109836985019729017715780112040458649153935115783499546100636635745448508241888279067531359950519206222976015376529797308588164873117308237059828489404487403932053592935976454165560795472477862029969232956138971989467942218727360512336559521133108778758228879597580320459608479024506385194174312616377510459921102486879496341706862092908893068525234805692599833377510390101316617812305114571932706629167125446512151746802548190358351688971707570677865618800822034683632101813026232996027599403579997774046244952114531588370357904483293150007246173417355805567832153454341170020258560809166294198637401514569572272836921963229511187762530753402594781448204657460288485500062806934811398276016855584079542162057543557291510641537592939022884356120792643705560062367986544382464373946972471945996555795505838034825597839682776084731530251788951718630722761103630509360074262261717363058613291544024695432904616258691774630578507674937487992329181750163484068813465534370997589353607405172909412697657593295156818624747127636468836551757018353417274662607306510451195762866349922848678780591085118985653555434958761664016447588028633629704046289097067736256584300235314749461233912068632146637087844699210427541569410912246568571204717241133378489816764096924981633421176857150311671040068175303192115415611958042570658693127276213710697472226029655524611053715554532499750843275200199214301910505362996007042963297805103066650638786268157658772683745128976850796366371059380911225428835839194121154773759981301921650952140133306070987313732926518169226845063443954056729812031546392324981793780469103793422169495229100793029949237507299325063050942813902793084134473061411643355614764093104425918481363930542369378976520526456347648318272633371512112030629233889286487949209737847861884868260804647319539200840398308008803869049557419756219293922110825766397681361044490024720948340326796768837621396744075713887292863079821849314343879778088737958896840946143415927131757836511457828935581859902923534388888846587452130838137779443636119762839036894595760120316502279857901545344747352706972851454599861422902737291131463782045516225447535356773622793648545035710208644541208984235038908770223039849380214734809687433336225449150117411751570704561050895274000206380497967960402617818664481248547269630823473377245543390519841308769781276565916764229022948181763075710255793365008152286383634493138089971785087070863632205869018938377766063006066757732427272929247421295265000706646722730009956124191409138984675224955790729398495608750456694217771551107346630456603944136235888443676215273928597072287937355966723924613827468703217858459948257514745406436460997059316120596841560473234396652457231650317792833860590388360417691428732735703986803342604670071717363573091122981306903286137122597937096605775172964528263757434075792282180744352908669606854021718597891166333863858589736209114248432178645039479195424208191626088571069110433994801473013100869848866430721216762473119618190737820766582968280796079482259549036328266578006994856825300536436674822534603705134503603152154296943991866236857638062351209884448741138600171173647632126029961408561925599707566827866778732377419444462275399909291044697716476151118672327238679208133367306181944849396607123345271856520253643621964198782752978813060080313141817069314468221189275784978281094367751540710106350553798003842219045508482239386993296926659221112742698133062300073465628498093636693049446801628553712633412620378491919498600097200836727876650786886306933418995225768314390832484886340318940194161036979843833346608676709431643653538430912157815543512852077720858098902099586449602479491970687230765687109234380719509824814473157813780080639358418756655098501321882852840184981407690738507369535377711880388528935347600930338598691608289335421147722936561907276264603726027239320991187820407067412272258120766729040071924237930330972132364184093956102995971291799828290009539147382437802779051112030954582532888721146170133440385939654047806199333224547317803407340902512130217279595753863158148810392952475410943880555098382627633127606718126171022011356181800775400227516734144169216424973175621363128588281978005788832454534581522434937268133433997710512532081478345067139835038332901313945986481820272322043341930929011907832896569222878337497354301561722829115627329468814853281922100752373626827643152685735493223028018101449649009015529248638338885664893002250974343601200814365153625369199446709711126951966725780061891215440222487564601554632812091945824653557432047644212650790655208208337976071465127508320487165271577472325887275761128357592132553934446289433258105028633583669291828566894736223508250294964065798630809614341696830467595174355313224362664207197608459024263017473392225291248366316428006552870975051997504913009859468071013602336440164400179188610853230764991714372054467823597211760465153200163085336319351589645890681722372812310320271897917951272799656053694032111242846590994556380215461316106267521633805664394318881268199494005537068697621855231858921100963441012933535733918459668197539834284696822889460076352031688922002021931318369757556962061115774305826305535862015637891246031220672933992617378379625150999935403648731423208873977968908908369996292995391977217796533421249291978383751460062054967341662833487341011097770535898066498136011395571584328308713940582535274056081011503907941688079197212933148303072638678631411038443128215994936824342998188719768637604496342597524256886188688978980888315865076262604856465004322896856149255063968811404400429503894245872382233543101078691517328333604779262727765686076177705616874050257743749983775830143856135427273838589774133526949165483929721519554793578923866762502745370104660909382449626626935321303744538892479216161188889702077910448563199514826630802879549546453583866307344423753319712279158861707289652090149848305435983200771326653407290662016775706409690183771201306823245333477966660525325490873601961480378241566071271650383582257289215708209369510995890132859490724306183325755201208090007175022022949742801823445413711916298449914722254196594682221468260644961839254249670903104007581488857971672246322887016438403908463856731164308169537326790303114583680575021119639905615169154708510459700542098571797318015564741406172334145847111268547929892443001391468289103679179216978616582489007322033591376706527676521307143985302760988478056216994659655461379174985659739227379416726495377801992098355427866179123126699374730777730569324430166839333011554515542656864937492128687049121754245967831132969248492466744261999033972825674873460201150442228780466124320183016108232183908654771042398228531316559685688005226571474428823317539456543881928624432662503345388199590085105211383124491861802624432195540433985722841341254409411771722156867086291742124053110620522842986199273629406208834754853645128123279609097213953775360023076765694208219943034648783348544492713539450224591334374664937701655605763384697062918725745426505879414630176639760457474311081556747091652708748125267159913793240527304613693961169892589808311906322510777928562071999459487700611801002296132304588294558440952496611158342804908643860880796440557763691857743754025896855927252514563404385217825890599553954627451385454452916761042969267970893580056234501918571489030418495767400819359973218711957496357095967825171096264752068890806407651445893132870767454169607107931692704285168093413311046353506242209810363216771910420786162184213763938194625697286781413636389620123976910465418956806197323148414224550071617215851321302030684176087215892702098879108938081045903397276547326416916845445627600759561367103584575649094430692452532085003091068783157561519847567569191284784654692558665111557913461272425336083635131342183905177154511228464455136016013513228948543271504760839307556100908786096663870612278690274831819331606701484957163004705262228238406266818448788374548131994380387613830128859885264201992286188208499588640888521352501457615396482647451025902530743172956899636499615707551855837165935367125448515089362904567736630035562457374779100987992499146967224041481601289530944015488942613783140087804311431741858071826185149051138744831358439067228949408258286021650288927228387426432786168690381960530155894459451808735197246008221529343980828254126128257157209350985382800738560472910941184006084485235377833503306861977724501886364070344973366473100602018128792886991861824418453968994777259482169137133647470453172979809245844361129618997595696240971845564020511432589591844724920942930301651488713079802102379065536525154780298059407529440513145807551537794861635879901158192019808879694967187448224156836463534326160242632934761634458163890163805123894184523973421841496889262398489648642093409816681494771155177009562669029850101513537599801272501241971119871526593747484778935488777815192931171431167444773882941064615028751327709474504763922874890662989841540259350834035142035136168819248238998027706666916342133424312054507359388616687691188185776118135771332483965209882085982391298606386822804754362408956522921410859852037330544625953261340234864689275060526893755148403298542086991221052597005628576707702567695300978970046408920009852106980295419699802138053295798159478289934443245491565327845223840551240445208226435420656313310702940722371552770504263482073984454889589248861397657079145414427653584572951329719091947694411910966797474262675590953832039169673494261360032263077428684105040061351052194413778158095005714526846009810352109249040027958050736436961021241137739717164869525493114805040126568351268829598413983222676377804500626507241731757395219796890754825199329259649801627068665658030178877405615167159731927320479376247375505855052839660294566992522173600874081212014209071041937598571721431338017425141582491824710905084715977249417049320254165239323233258851588893337097136310892571531417761978326033750109026284066415801371359356529278088456305951770081443994114674291850360748852366654744869928083230516815711602911836374147958492100860528981469547750812338896943152861021202736747049903930417035171342126923486700566627506229058636911882228903170510305406882096970875545329369434063981297696478031825451642178347347716471058423238594580183052756213910186997604305844068665712346869679456044155742100039179758348979935882751881524675930878928159243492197545387668305684668420775409821781247053354523194797398953320175988640281058825557698004397120538312459428957377696001857497335249965013509368925958021863811725906506436882127156815751021712900765992750370228283963962915973251173418586721023497317765969454283625519371556009143680329311962842546628403142444370648432390374906410811300792848955767243481200090309888457270907750873638873299642555050473812528975962934822878917619920725138309388288292510416837622758204081918933603653875284116785703720989718832986921927816629675844580174911809119663048187434155067790863948831489241504300476704527971283482211522202837062857314244107823792513645086677566622804977211397140621664116324756784216612961477109018826094677377686406176721484293894976671380122788941309026553511096118347012565197540807095384060916863936906673786627209429434264260402902158317345003727462588992622049877121178405563348492490326003508569099382392777297498413565614830788262363322368380709822346012274241379036473451735925215754757160934270935192901723954921426490691115271523338109124042812102893738488167358953934508930697715522989199698903885883275409044300321986834003470271220020159699371690650330547577095398748580670024491045504890061727189168031394528036165633941571334637222550477547460756055024108764382121688848916940371258901948490685379722244562009483819491532724502276218589169507405794983759821006604481996519360110261576947176202571702048684914616894068404140833587562118319210838005632144562018941505945780025318747471911604840677997765414830622179069330853875129298983009580277554145435058768984944179136535891620098725222049055183554603706533183176716110738009786625247488691476077664470147193074476302411660335671765564874440577990531996271632972009109449249216456030618827772947750764777446452586328919159107444252320082918209518021083700353881330983215894608680127954224752071924134648334963915094813097541433244209299930751481077919002346128122330161799429930618800533414550633932139339646861616416955220216447995417243171165744471364197733204899365074767844149929548073025856442942381787641506492878361767978677158510784235702640213388018875601989234056868423215585628508645525258377010620532224244987990625263484010774322488172558602233302076399933854152015343847725442917895130637050320444917797752370871958277976799686113626532291118629631164685159934660693460557545956063155830033697634000276685151293843638886090828376141157732003527565158745906567025439437931104838571313294490604926582363108949535090082673154497226396648088618041573977888472892174618974189721700770009862449653759012727015227634510874906948012210684952063002519011655963580552429180205586904259685261047412834518466736938580027700252965356366721619883672428226933950325930390994583168665542234654857020875504617520521853721567282679903418135520602999895366470106557900532129541336924472492212436324523042895188461779122338069674233980694887270587503389228395095135209123109258159006960395156367736067109050566299603571876423247920752836160805597697778756476767210521222327184821484446631261487584226092608875764331731023263768864822594691211032367737558122133470556805958008310127481673962019583598023967414489867276845869819376783757167936723213081586191045995058970991064686919463448038574143829629547131372173669836184558144505748676124322451519943362182916191468026091121793001864788050061351603144350076189213441602488091741051232290357179205497927970924502479940842696158818442616163780044759478212240873204124421169199805572649118243661921835714762891425805771871743688000324113008704819373962295017143090098476927237498875938639942530595331607891618810863505982444578942799346514915952884869757488025823353571677864826828051140885429732788197765736966005727700162592404301688659946862983717270595809808730901820120931003430058796552694788049809205484305467611034654748067290674399763612592434637719995843862812391985470202414880076880818848087892391591369463293113276849329777201646641727587259122354784480813433328050087758855264686119576962172239308693795757165821852416204341972383989932734803429262340722338155102209101262949249742423271698842023297303260161790575673111235465890298298313115123607606773968998153812286999642014609852579793691246016346088762321286205634215901479188632194659637483482564291616278532948239313229440231043277288768139550213348266388687453259281587854503890991561949632478855035090289390973718988003999026132015872678637873095678109625311008054489418857983565902063680699643165033912029944327726770869305240718416592070096139286401966725750087012218149733133695809600369751764951350040285926249203398111014953227533621844500744331562434532484217986108346261345897591234839970751854223281677187215956827243245910829019886390369784542622566912542747056097567984857136623679023878478161201477982939080513150258174523773529510165296934562786122241150783587755373348372764439838082000667214740034466322776918936967612878983488942094688102308427036452854504966759697318836044496702853190637396916357980928865719935397723495486787180416401415281489443785036291071517805285857583987711145474240156416477194116391354935466755593592608849200546384685403028080936417250583653368093407225310820844723570226809826951426162451204040711501448747856199922814664565893938488028643822313849852328452360667045805113679663751039248163336173274547275775636810977344539275827560597425160705468689657794530521602315939865780974801515414987097778078705357058008472376892422189750312758527140173117621279898744958406199843913365680297721208751934988504499713914285158032324823021340630312586072624541637765234505522051086318285359658520708173392709566445011404055106579055037417780393351658360904543047721422281816832539613634982525215232257690920254216409657452618066051777901592902884240599998882753691957540116954696152270401280857579766154722192925655963991820948894642657512288766330302133746367449217449351637104725732980832812726468187759356584218383594702792013663907689741738962252575782663990809792647011407580367850599381887184560094695833270775126181282015391041773950918244137561999937819240362469558235924171478702779448443108751901807414110290370706052085162975798361754251041642244867577350756338018895379263183389855955956527857227926155524494739363665533904528656215464288343162282921123290451842212532888101415884061619939195042230059898349966569463580186816717074818823215848647734386780911564660755175385552224428524049468033692299989300783900020690121517740696428573930196910500988278523053797637940257968953295112436166778910585557213381789089945453947915927374958600268237844486872037243488834616856290097850532497036933361942439802882364323553808208003875741710969289725499878566253048867033095150518452126944989251596392079421452606508516052325614861938282489838000815085351564642761700832096483117944401971780149213345335903336672376719229722069970766055482452247416927774637522135201716231722137632445699154022395494158227418930589911746931773776518735850032318014432883916374243795854695691221774098948611515564046609565094538115520921863711518684562543275047870530006998423140180169421109105925493596116719457630962328831271268328501760321771680400249657674186927113215573270049935709942324416387089242427584407651215572676037924765341808984312676941110313165951429479377670698881249643421933287404390485538222160837088907598277390184204138197811025854537088586701450623578513960109987476052535450100439353062072439709976445146790993381448994644609780957731953604938734950026860564555693224229691815630293922487606470873431166384205442489628760213650246991893040112513103835085621908060270866604873585849001704200923929789193938125116798421788115209259130435572321635660895603514383883939018953166274355609970015699780289236362349895374653428746875
Теперь другой подход, который я применил, - это Divide и Concur через рекурсию.
т.е. Fib(n) = fib(n-1) + Fib(n-2), а затем дальнейшая рекурсия для n-1 и n-2..... до 2 и 1., которые запрограммированы как -
package com.company.dynamicProgramming;
import java.math.BigInteger;
public class FibonacciByBigDecimal {
public static void main(String ...args) {
int n = 100000;
BigInteger[] fibOfnS = new BigInteger[n + 1];
System.out.println("fibonacci of "+ n + " is : " + fibByDivCon(n, fibOfnS));
}
static BigInteger fibByDivCon(int n, BigInteger[] fibOfnS){
if(fibOfnS[n]!=null){
return fibOfnS[n];
}
if (n == 1 || n== 2){
fibOfnS[n] = BigInteger.ONE;
return BigInteger.ONE;
}
// creates 2 further entries in stack
BigInteger fibOfn = fibByDivCon(n-1, fibOfnS).add( fibByDivCon(n-2, fibOfnS)) ;
fibOfnS[n] = fibOfn;
return fibOfn;
}
}
Когда я запустил код для n = 100000, результат будет следующим:
Exception in thread "main" java.lang.StackruError
at com.company.dynamicProgramming.FibonacciByBigDecimal.fibByDivCon(FibonacciByBigDecimal.java:29)
at com.company.dynamicProgramming.FibonacciByBigDecimal.fibByDivCon(FibonacciByBigDecimal.java:29)
at com.company.dynamicProgramming.FibonacciByBigDecimal.fibByDivCon(FibonacciByBigDecimal.java:29)
Выше вы можете видеть, что создается StackruError. Теперь причина этого - слишком много рекурсий, так как -
// creates 2 further entries in stack
BigInteger fibOfn = fibByDivCon(n-1, fibOfnS).add( fibByDivCon(n-2, fibOfnS)) ;
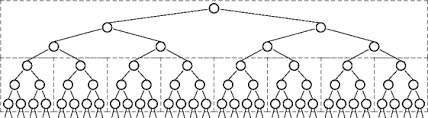
Таким образом, каждая запись в стеке создает еще 2 записи и так далее... что представлено как -
В конце концов будет создано так много записей, что система не сможет обработать их в стеке и вызовет StackruError.
Для предотвращения: Для приведенного выше примера - 1. Избегайте использования подхода рекурсии или уменьшайте / ограничивайте рекурсию снова на одно деление уровня, например, если n слишком велико, тогда разделите n, чтобы система могла справиться с его пределом.2. Используйте другой подход, например, цикл, который я использовал в первом примере кода. (Я вовсе не собираюсь ухудшать Divide & Concur или Recursion, поскольку они являются легендарными подходами во многих самых известных алгоритмах... я намерен ограничить рекурсию или держаться подальше от нее, если я подозреваю проблемы с переполнением стека)
Какие? Ни у кого нет любви к тем, кого охватывает бесконечный цикл?
do
{
JeffAtwood.WritesCode();
} while(Stackru.MakingMadBank.Equals(false));
Учитывая, что это было помечено как "взлом", я подозреваю, что "переполнение стека", на которое он ссылается, является переполнением стека вызовов, а не переполнением стека более высокого уровня, подобным тем, на которые ссылаются в большинстве других ответов здесь. На самом деле это не относится ни к каким управляемым или интерпретируемым средам, таким как.NET, Java, Python, Perl, PHP и т. Д., В которые обычно пишутся веб-приложения, поэтому ваш единственный риск - это сам веб-сервер, который, вероятно, написан на С или С ++.
Проверьте эту тему:
https://stackru.com/questions/7308/what-is-a-good-starting-point-for-learning-buffer-overflow
Переполнение стека происходит, когда ваша программа использует весь стек. Чаще всего это происходит, когда ваша программа имеет рекурсивную функцию, которая всегда вызывает сама себя. Каждый новый вызов рекурсивной функции занимает больше стека, пока в конечном итоге ваша программа не использует весь стек.