Решить х с помощью линейной системы, используя решение () в г

Question

Я пытаюсь преобразовать это уравнение в линейную системную задачу, а затем получить x с помощью метода execute() в r. Тем не менее, у меня есть некоторые проблемы в трансформации. Уравнение: (t(A)%*%t(R)-I)%*%x = -(t(q)%*%x)%*% l

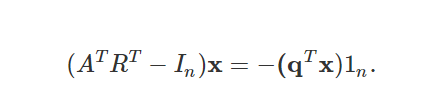
где A - матрица 500 * 500, R - матрица 500 * 500, I - единичная матрица 500 * 500, q - вектор 500*1, l - вектор 500*1, все элементы равны 1.

Я пытаюсь переместить х в левую сторону и не знаю, как это сделать. Может кто-нибудь помочь с этим? Спасибо!

Answer 1

Это уравнение, очевидно, имеет тривиальное решение x=0, С другой стороны, для того чтобы он имел нетривиальные решения, нужно переставить уравнение в задачу на собственные значения и найти x соответствует любому собственному значению, равному нулю (по крайней мере, с точностью до числовой точности).

Если вы переставите правую часть уравнения, чтобы она была внешним произведением 1_n и q, умноженного на xтогда уравнение принимает вид M*x=0. Если вы выполните собственное разложение M (которое по сути является [AR-I-1q]), надеюсь, вы найдете некоторые собственные значения, близкие к нулю. Имейте в виду, что эта матрица вполне может быть не симметричной, поэтому собственные значения могут быть сложными.