Как объединить систему ODE с системой FEM
У меня есть динамическая модель, настроенная как (жесткая) система ODE. В настоящее время я решаю это с помощью CVODE (из пакета SUNDIALS в пакете Python Assimulo), и все хорошо.
Теперь я хочу добавить новый 3D-радиатор (с температурно-зависимыми тепловыми параметрами) к этой проблеме. Вместо того, чтобы выписывать все уравнения с нуля для трехмерного уравнения теплопроводности, моя идея состоит в том, чтобы использовать существующую структуру FEM или FVM, чтобы предоставить мне интерфейс, который позволит мне легко обеспечить (t, y) для 3D-блока в рутину, и вернуть остатки y', Принцип состоит в том, чтобы использовать уравнения из системы FEM, но не решатель. CVODE может эксплуатировать разреженность, но ожидается, что объединенная система будет решать медленнее, чем система FEM, решая сама, с учетом этого.
# pseudocode of a residuals function for CVODE
def residual(t, y):
# ODE system of n equations
res[0] = <function of t,y>;
res[1] = <function of t,y>;
...
res[n] = <function of t,y>;
# Here we add the FEM/FVM residuals
for i in range(FEMcount):
res[n+1+i] = FEMequations[FEMcount](t,y)
return res
Мой вопрос заключается в том, является ли (а) этот подход разумным, и (б) существует ли библиотека FEM или FVM, которая позволит мне легко рассматривать ее как систему уравнений, так что я могу "привязать" ее к своему существующему набору Уравнения ОДУ.
Если не удается разрешить двум системам использовать одну и ту же временную ось, мне придется запустить их в пошаговом режиме, где я в течение короткого времени запускаю одну модель, обновляю граничные условия для другой, запускаю ту, обновляю BC первой модели и так далее.
У меня есть некоторый опыт работы с замечательной библиотекой FiPy, и я ожидаю в конечном итоге использовать эту библиотеку описанным выше способом. Но я хочу узнать об опыте с другими системами в задачах такого рода, а также о других подходах, которые я пропустил.
Изменить: Теперь у меня есть пример кода, который, кажется, работает, показывая, как остатки диффузии сетки FiPy могут быть решены с помощью CVODE. Тем не менее, это только один подход (с использованием FiPy), а остальные мои другие вопросы и проблемы остаются в силе. Любые предложения приветствуются.
from fipy import *
from fipy.solvers.scipy import DefaultSolver
solverFIPY = DefaultSolver()
from assimulo.solvers import CVode as solverASSIMULO
from assimulo.problem import Explicit_Problem as Problem
# FiPy Setup - Using params from the Mesh1D example
###################################################
nx = 50; dx = 1.; D = 1.
mesh = Grid1D(nx = nx, dx = dx)
phi = CellVariable(name="solution variable", mesh=mesh, value=0.)
valueLeft, valueRight = 1., 0.
phi.constrain(valueRight, mesh.facesRight)
phi.constrain(valueLeft, mesh.facesLeft)
# Instead of eqX = TransientTerm() == ExplicitDiffusionTerm(coeff=D),
# Rather just operate on the diffusion term. CVODE will calculate the
# Transient side
edt = ExplicitDiffusionTerm(coeff=D)
timeStepDuration = 0.9 * dx**2 / (2 * D)
steps = 100
# For comparison with an analytical solution - again,
# taken from the Mesh1D.py example
phiAnalytical = CellVariable(name="analytical value", mesh=mesh)
x = mesh.cellCenters[0]
t = timeStepDuration * steps
from scipy.special import erf
phiAnalytical.setValue(1 - erf(x / (2 * numerix.sqrt(D * t))))
if __name__ == '__main__':
viewer = Viewer(vars=(phi, phiAnalytical))#, datamin=0., datamax=1.)
viewer.plot()
raw_input('Press a key...')
# Now for the Assimulo/Sundials solver setup
############################################
def residual(t, X):
# Pretty straightforward, phi is the unknown
phi.value = X # This is a vector, 50 elements
# Can immediately return the residuals, CVODE sees this vector
# of 50 elements as X'(t), which is like TransientTerm() from FiPy
return edt.justResidualVector(var=phi, solver=solverFIPY)
x0 = phi.value
t0 = 0.
model = Problem(residual, x0, t0)
simulation = solverASSIMULO(model)
tfinal = steps * timeStepDuration # s,
cell_tol = [1.0e-8]*50
simulation.atol = cell_tol
simulation.rtol = 1e-6
simulation.iter = 'Newton'
t, x = simulation.simulate(tfinal, 0)
print x[-1]
# Write back the answer to compare
phi.value = x[-1]
viewer.plot()
raw_input('Press a key...')
Это даст график, показывающий идеальное совпадение:
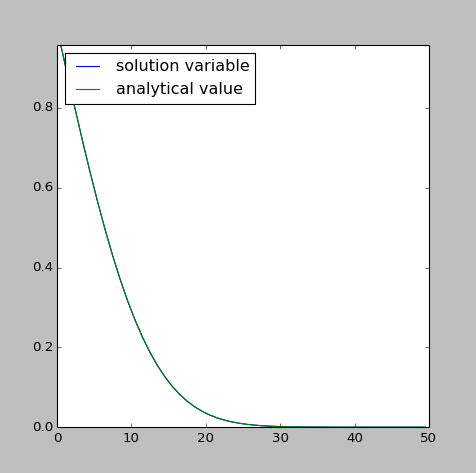
1 ответ
ODE - это дифференциальное уравнение в одном измерении.
Модель FEM предназначена для пространственных проблем, т. Е. Для задач в более высоких измерениях. Вы хотите метод конечных разностей. Проще понять и понять с точки зрения кого-то из мира ODE.
Вопрос, который, я думаю, вам действительно следует задать, заключается в том, как вы берете свой ODE и переносите его в трехмерное проблемное пространство.
Многомерные уравнения в частных производных трудно решить, но я отсылаю вас к методу CFD для выполнения этого, однако, только в 2D. http://lorenabarba.com/blog/cfd-python-12-steps-to-navier-stokes/
Чтобы пройти через это, у вас должен быть полдень! Удачи!