Деформации CUDA и расхождение нитей

Question

Я пытаюсь понять перекосы CUDA и расхождение потоков. Предположим, у меня есть ядро ​​умножения наивных матриц для умножения матриц nxn.

__global__ void matrix_multiply(float* a, float* b, float* c, int n)
{
    int row = blockIdx.y + blockDim.y + threadIdx.y;
    int col = blockIdx.x + blockDim.x + threadIdx.x;

    if(row < n && col < n) {
        float tmp = 0.0f;
        for(int i = 0; i < n; ++i)
            tmp += a[row * n + i] * b[i * n + col];
        c[row * n + col] = tmp;
    }
}

Если я запускаю ядро ​​с размером сетки 32 на 32 и размером блока 16 на 16, а матрицы имеют размер 500 на 500, сколько перекосов имеют потоки, которые столкнутся с расхождением потоков?

Поскольку каждый блок потока по правому краю матрицы будет иметь дивергенцию потока, не должно ли число перекосов с дивергенцией потока быть 256?

Answer 1

В вашем коде есть две потенциальные точки расхождения. Первый может быть создан if заявление и второе по условию в for петля. Второй безвреден с точки зрения расхождения деформации, так как вход n равномерно по всем потокам.

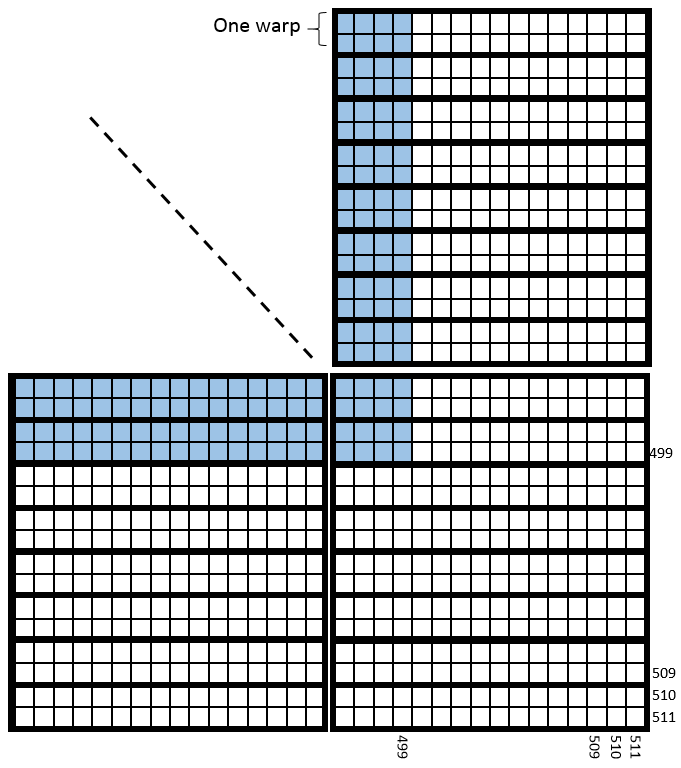
Во-первых, те потоки, которые не удовлетворяют условию, быстро завершатся. Если n 500, что, по-видимому, число быстро существующих потоков составляет (16*16)*(32*32)-(500*500)=12144. Имея в виду ответ на этот вопрос, существует 250 перекосов, сталкивающихся с дивергенцией, каждый из которых состоит из двух рядов по 16 * 16 самых верхних блоков, проходящих через правый край. В каждом из них полосы с идентификаторами 0, 1, 2, 3, 16, 17, 18 и 19 удовлетворяют условию и попадают в if блок пока остальные отключены. Там будет 6*(512/16)=192 деформации, которые if условие будет ложным для всех их линий, следовательно, они не сталкиваются с расхождением.

На рисунке ниже показано, что происходит в самом нижнем правом углу.