Числа Хэмминга по интервалам

Question

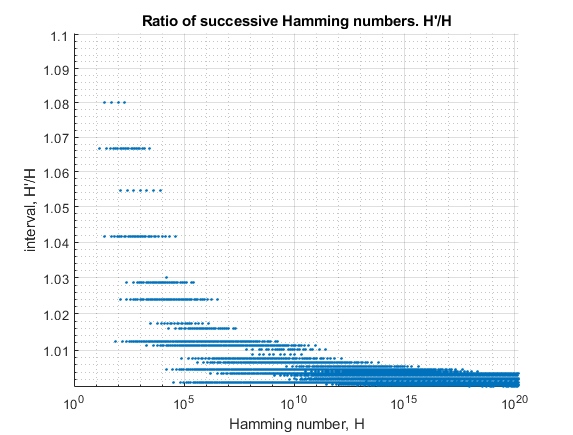
Вот несколько иной подход к генерации последовательности чисел Хэмминга (или обычных чисел, 5-гладких чисел) на основе интервала от одного числа в последовательности до следующего. Вот пример графика указанных интервалов:

Таким образом, существует относительно ограниченное количество дискретных интервалов, отделяющих одно число от следующего, и интервалы становятся меньше по мере увеличения H. Часто отмечается, что числа Хэмминга становятся более разреженными по мере увеличения их размера, что они и делают в абсолютном выражении, но в другом смысле (пропорционально) они сближаются.

В основном, когда H поднимается, появляется большая возможность для 2^i*3^j*5^k, где i,j,k - положительные или отрицательные целые числа, чтобы получить дробь около 1,0.

Оказывается, что таблица всего из 119 интервалов (i,j,k троек) охватывает числа Хэмминга примерно до 10^10000. Это примерно первые 1,59 триллиона чисел Хэмминга. Такая таблица (файл заголовка C), отсортированная по размеру интервала от малого к большому, находится здесь. Учитывая число Хэмминга, чтобы найти следующее, все, что требуется, - это найти первую запись в таблице, где умножение (сложение соответствующих показателей) даст результат с положительными степенями для i, j и k.

Например, миллионное число Хэмминга составляет 2^55*3^47*5^64, что составляет около 5,1931278e83. Следующее число Хэмминга после этого - 2^38*3^109*5^29 или около 5.1938179e83. Первая соответствующая запись в таблице:

{-17,62, -35}, // 1.000132901540844

Таким образом, хотя эти числа разделены примерно на 7e79, их соотношение составляет 1,000132901540844. Чтобы найти следующий номер, нужно просто попробовать до 119 записей в худшем случае, включая только сложения и сравнения (без умножений). Кроме того, таблица только из 3 коротких целых для каждой записи требует менее 1 КБ памяти. Алгоритм в основном O(1) в памяти и O(n) во времени, где n - длина последовательности.

Одним из способов его ускорения было бы вместо того, чтобы каждый раз искать таблицу по 0-му индексу, ограничивать список записей таблицы поиском только тех записей, которые эмпирически известны как преемники данной записи в данном диапазоне (n < 1,59). e12). Эти списки приведены в заголовочном файле выше в структуре succtab[], например:

{11, {47,55,58,65,66,68,70,72,73,75,76}},

Таким образом, эмпирически установлено, что за этим конкретным индексом следуют только 11 различных индексов, так что это единственные из них, которые искали.

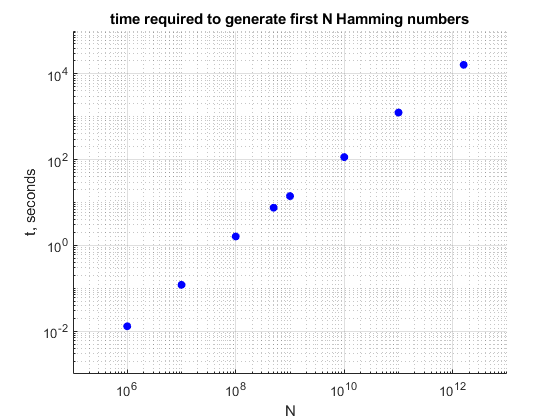
Это ускоряет алгоритм в 4 раза или около того, реализованный здесь (код C) вместе с заголовочным файлом выше. Вот график времени выполнения на i7-2600 с частотой 3,4 ГГц:

Я считаю, что это выгодно отличается от уровня техники - так ли это?

Задача Хэмминга иногда сводится к простому нахождению n-го числа Хэмминга без генерации всех промежуточных значений. Адаптация вышеупомянутой методики к известной схеме простого перечисления чисел Хэмминга в полосе вокруг желаемого диапазона дает этот график времени выполнения: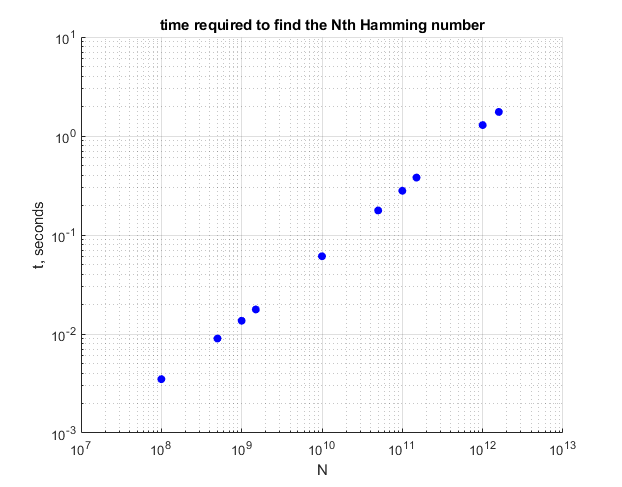

Так что это займет менее 2 секунд, чтобы найти 1,59 триллионное число Хэмминга. Код C для этого здесь. Это также выгодно отличается от уровня техники, по крайней мере, в данных пределах?

РЕДАКТИРОВАТЬ: границы для n (1,59e12, числа Хэмминга примерно до 10^10000) были выбраны на основе конкретной машины, где было желательно, чтобы i,j,k были короткие целые, а также разумное ожидание скорости выполнения. Могут быть сгенерированы таблицы большего размера, например, таблица из 200 записей позволила бы достичь значения n, равного примерно 1e18 (числа Хэмминга до 10^85000).

Другой вопрос будет, как ускорить это дальше. Одна потенциальная область: оказывается, что некоторые записи таблицы встречаются гораздо чаще, чем другие, и у них есть соответственно больший список преемников для проверки. Например, при генерации первых чисел 1.59e12 на эту запись попадают полностью 46% итераций:

{} -7470,2791,1312

У него 23 возможных разных преемника. Возможно, какой-то способ сузить это на основе других параметров (например, история предыдущих записей), хотя не было бы много места для дорогостоящей операции.

РЕДАКТИРОВАТЬ № 2:

Для некоторой информации о генерации таблицы, в основном, есть шесть классов дробей 2^i*3^j*5^k, где i,j,k - положительные или отрицательные целые числа: дроби с только 2,3 или 5 в числителе, и дроби только с 2,3 или 5 в знаменателе. Например, для класса с только 2 в числителе:

f = 2 ^ i / (3 ^ j * 5 ^ k), i> 0 и j,k >= 0

Программа A C для вычисления интервалов для этого класса дроби находится здесь. Для чисел Хэмминга примерно до 10 10000 он запускается за несколько секунд. Возможно, это можно сделать более эффективным.

Повторение аналогичного процесса для остальных 5 классов дробей дает шесть списков. Сортировка их всех вместе по размеру интервала и удаление дубликатов дает полную таблицу.

Answer 1

Перечисление троек составляет ~ n^2/3, но сортировка полосы составляет ~ n^2/3 log (n^2/3), т.е. ~ n^2/3 log n. Это, очевидно, не меняется даже при использовании схемы ~ n^1/3 зоны.

Действительно, эмпирические сложности на практике рассматриваются как ~ n^0,7.

Мне еще предстоит полностью понять ваш алгоритм, но представленные вами данные настоятельно предполагают чистую операцию ~ n^2/3, которая, безусловно, представляет собой явное и значительное улучшение по сравнению с предыдущим уровнем техники.

На мой взгляд, это было бы не так, если бы нужно было генерировать всю последовательность, чтобы найти "интервалы" (отношения), на которых основан ваш алгоритм. Но поскольку вы генерируете их независимо, как, по-видимому, предполагает ваше последующее редактирование, это не мешает вообще.

Исправление: если нас интересует только n- й член последовательности, то полная сортировка полосы не нужна; O (n) алгоритмывыбора k-го числа существуют.