Докажи это! не находится в O(n^p) для любого постоянного натурального числа p

Question

Как я могу доказать, что п! не в O(n^p) для любого постоянного натурального числа p? И есть (n k)(n выбрать k) в O(n^p) для всех k?

Answer 1

Приближение Стерлинга говорит, что

log (n!) = n log n - n + O(log n) = O(n log n)

Но

log (n^p) = p log n = O(log n)

для постоянного p, очевидно n! растет быстрее чем n^p и, следовательно, это не O(n^p),

Answer 2

Вы можете доказать, что п! не находится в O(n^p) для любого постоянного натурального числа p, показывая, что вы всегда можете выбрать n (для фиксированной константы p), так что n! > n^p,

(чтобы понять, выберите несколько низких значений p и нанесите n! против n ^ p)

Рассуждения для второй части следуют тем же строкам. Связать (n выбрать k), а затем использовать первую часть.

Подсказка: как отметил Касабланка, вы можете использовать приближение Стирлинга

Answer 3

Редактировать (3/2011) - более простой метод, использующий только простое исчисление

Один из способов показать, что O (n!) Не равно O(n^p), - сравнить журнал n! с журналом п ^ р.

ln(n!) = сумма (ln(i)) {i: 1 до n}

ln (n ^ p) = p * ln (n)

Это не помогает, так как мы не знаем, какова будет сумма логов. Хитрость заключается в том, чтобы вычислить нижнюю границу, используя интеграл от ln (i) di от 1 до n

На изображении ниже видно, что чернота ln(x) меньше, чем функция шага суммы синего цвета.

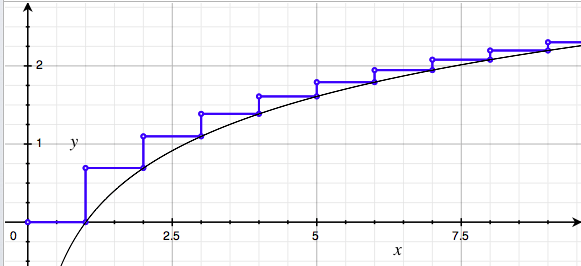
Учитывая, что неопределенный интеграл от ln (i) di равен i*ln(i) - i + C, мы можем интегрировать от 1 до n, чтобы получить:

n * ln (n) - n + 1 в качестве нижней границы.

И потому что нельзя выбрать p, которое больше всех возможных n:

O (pln (n)) ln(n)), O(n^p)

примечание: интегрирование ln (n) для получения приближения к ln(n!) является основой для приближения Стирлинга. Это приблизительное приближение, и если вы продолжите его, взяв антилог: n! >= e*(n/e)^n, тогда как у Стирлинга вместо e - sqrt(2*pi*n).

Интегрирование от 1 до n + 1 даст вам верхнюю границу (функция шага суммы будет вписываться в график ln (n))