Почему я получаю только NaN и Inf при моделировании ODE45 в Октаве?
Я использую Octave с ODE45 для моделирования системы уравнений ODE. Но проблема в том, что моделирование ODE дает неправильные значения. Посмотрите на этот код Octave:
function dx = dynamik(t, x)
b1 = 1000;
b2 = 2000;
m1 = 10;
m2 = 7;
M = 2000;
g = 9.82;
mu = 0.3;
L = 0.1;
Ap = 0.004;
Am = 0.002;
Pp = 2*10^6;
Pm = 2.1*10^6;
k1 = 1.78e+4;
k2 = 4.04e+4;
k3 = 8.86e+3;
dx= [ x(2);
-k1/m1*x(1) + k1/m1*x(3) - b1/m1*x(4) + b1/m1*x(4) + Ap/m1*Pp - Pm*Am/m1*x(2);
x(4);
k1/M*x(1) - k1/M*x(3) + b1/M*x(2) - b1/M*x(4) - g*mu*x(4) - k2/M*x(3) + k3*L/M*sin(x(5));
x(6);
3*k2/(m2*L)*x(3) - 3*k2/m2*sin(x(5)) - 3*k3/(m2*L^2)*x(5) - 3*b2/(m2*L^2)*x(6) + 3*g/(2*L)*sin(x(5))];
endfunction
tspan = 0:0.5:10;
init = [0, 0, 0, 0, 0, 0];
[t, y] = ode45(@dynamik, tspan, init);
Это дает:
>> y
y =
0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00 0.0000e+00
1.6659e+08 -6.9253e+10 -1.9336e+05 8.0380e+07 -4.4787e+07 3.8388e+12
5.9331e+18 -2.4665e+21 -6.8864e+15 2.8628e+18 -1.3333e+32 1.1428e+37
2.1131e+29 -8.7843e+31 -2.4526e+26 1.0196e+29 -3.9691e+56 3.4019e+61
7.5258e+39 -3.1286e+42 -8.7350e+36 3.6313e+39 -1.1816e+81 1.0127e+86
2.6803e+50 -1.1142e+53 -3.1110e+47 1.2933e+50 -3.5174e+105 3.0148e+110
9.5460e+60 -3.9684e+63 -1.1080e+58 4.6060e+60 -1.0471e+130 8.9747e+134
3.3998e+71 -1.4134e+74 -3.9461e+68 1.6404e+71 -3.1171e+154 2.6717e+159
1.2109e+82 -5.0337e+84 -1.4054e+79 5.8425e+81 -9.2794e+178 7.9533e+183
4.3125e+92 -1.7928e+95 -5.0054e+89 2.0808e+92 -2.7624e+203 2.3676e+208
1.5359e+103 -6.3849e+105 -1.7827e+100 7.4109e+102 -8.2234e+227 7.0482e+232
5.4701e+113 -2.2740e+116 -6.3491e+110 2.6394e+113 -2.4480e+252 2.0982e+257
1.9482e+124 -8.0989e+126 -2.2612e+121 9.4003e+123 -7.2875e+276 6.2461e+281
6.9386e+134 -2.8844e+137 -8.0534e+131 3.3479e+134 -2.1694e+301 1.8594e+306
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN NaN
Но в OpenModelica у меня есть этот код:
model Hydraulik_System_1
// Types for variables
type PositionCylinder = Real(unit="m");
type Position = Real(unit="m");
type Velocity = Real(unit="m/s");
type DegreesPosition = Real(unit="rad");
type DegreesVelocity = Real(unit="rad/s");
type pressure = Real(unit="Pa");
type flows = Real(unit="l/min", min=0.0);
// Types for parameters
type spring = Real(unit="N/m");
type damper = Real(unit="Ns/m");
type mass = Real(unit="kg");
type friction = Real(unit="%");
type length = Real(unit="m");
type gravitation = Real(unit="m/s^2");
type area = Real(unit="cm^2");
// Parameters
parameter spring k1 = 1.78*10^4;
parameter spring k2 = 4.04*10^4;
parameter spring k3 = 8.86*10^3;
parameter mass m1 = 10;
parameter mass m2 = 7;
parameter mass M = 2000;
parameter damper b1 = 1000;
parameter damper b2 = 2000;
parameter gravitation g = 9.82;
parameter friction mu = 0.3;
parameter area Am = 0.002;
parameter area Ap = 0.004;
parameter length L = 0.1;
parameter pressure Pp = 2*10^6;
parameter pressure Pm = 2.1*10^6;
// Variables
PositionCylinder x1;
Position x3;
Velocity x2 , x4;
DegreesPosition x5;
DegreesVelocity x6;
initial equation
x1 = 0;
x2 = 0;
x3 = 0;
x4 = 0;
x5 = 0;
x6 = 0;
equation
der(x1) = x2;
der(x2) = - k1/m1*x1 + k1/m1*x3 - b1/m1*x4 + b1/m1*x4 + Ap/m1*Pp - Pm*Am/m1*x2;
der(x3) = x4;
der(x4) = k1/M*x1 - k1/M*x3 + b1/M*x2 - b1/M*x4 - g*mu*x4 - k2/M*x3 + k3*L/M*sin(x5);
der(x5) = x6;
der(x6) = 3*k2/(m2*L)*x3 - 3*k2/m2*sin(x5) - 3*k3/(m2*L^2)*x5 - 3*b2/(m2*L^2)*x6 + 3*g/(2*L)*sin(x5);
end Hydraulik_System_1;
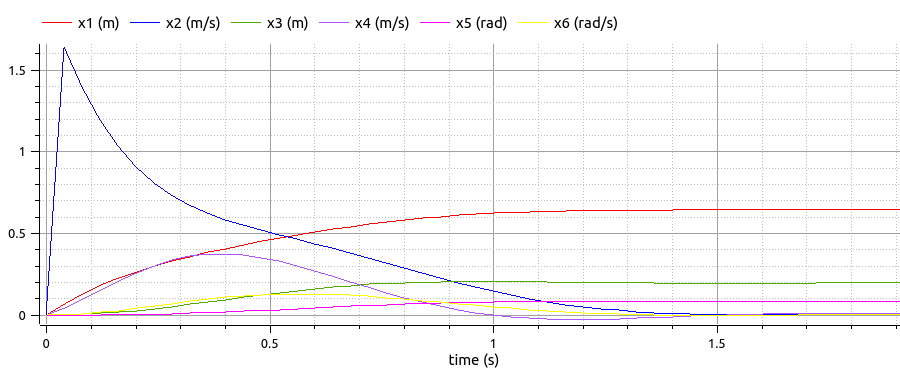
И результат выглядит так:
Можете ли вы сказать мне, почему это происходит с моими симуляциями? Существует огромная разница между результатом моделирования OpenModelica и результатом моделирования Octave. Зачем? Не имеет значения, если я изменю решатель ODE. Результаты будут почти такими же.
1 ответ
Я использовал lsode и тоже получил правильные ответы, но нужно было переключать параметры вызова и уменьшать tspan.
Сначала поменяйте местами параметры в функции:
function dx = dynamik(x, t)
Установить tspan:
tspan = 0:0.0625:2;
Тогда lsode вызов:
[y,t] = lsode(@dynamik, init, tspan );
Обновление: установлено odepkgи смог воспроизвести вашу ошибку. Также видел ошибку с ode23, но не с ode23s, Это указывает на то, что ваш ODE "жесткий", поэтому Runge-Kutta 4/5 не совсем подходящий алгоритм.