Поиск пути, имеющего подпуть и максимальный gcd (начальный узел, конечный узел)
Я получил вопрос в конкурсе (который закончился несколько недель назад). Вопрос, который я интерпретировал, был:
Дан неориентированный ациклический граф, который связан (N-1) ребрами и N узлами. Граф гарантированно будет подключен. Для двух узлов u и v необходимо найти два узла x и y графа, чтобы путь между этими двумя узлами полностью перекрывал путь между заданными городами u и v, а gcd(x, y) максимально возможен.
Ограничения
1 <= N <= 5 * 10 ^ 5
1 <= a,b, u, v <= N
где a,b - два произвольных узла в графе.
Пример пусть в графе 10 узлов (от 1 до 10)
Теперь в предыдущей строке я дам два целых числа a и b, что означает, что a и b напрямую связаны.
1 4
1 5
1 2
4 3
4 6
5 7
2 10
2 9
2 8
Наконец уф 4 2
Ответ - 4
Путь от u до v - 4 -> 1 -> 2
Теперь некоторые пути, которые полностью перекрывают путь от u к v:
4 -> 1 -> 2 -> 10
3 -> 4 -> 1 -> 2 -> 9
4 -> 1 -> 2 -> 8
и так далее....
Обратите внимание, что выбор пути от 4 до 8 полностью перекрывает путь u к v, а также gcd(4,8) = 4, что является максимально возможным.
График: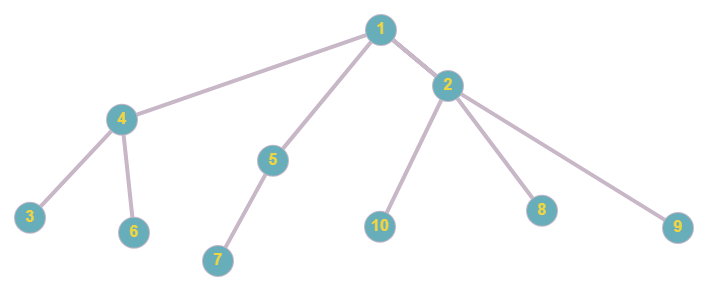 
Ограничение времени: 3.0 секунды
Мой подход к решению проблемы был:
Найдите путь от каждого узла к каждому другому узлу и сохраните его в списке массивов.
Переберите все списки и найдите, содержатся ли пути u и v в массиве.
Если путь найден, вычислите gcd начального и конечного узла и проверьте максимальный gcd.
Однако я думаю, что мой подход слишком груб, а код слишком длинный, и я думаю, что он слишком сложен.
Может ли кто-нибудь предложить какое-либо предложение или подход для решения этого вопроса?
1 ответ
Может быть, вы можете сделать DFS на начальной и конечной вершины и удалить из тех вершин, которые уже на подграфе. Теперь у вас есть все возможные вершины, которые могут быть частью решения. Проверьте все возможные комбинации из этих вершин и выберите пару с максимальным gcd. Во время выполнения dfs обязательно добавьте условие if, чтобы игнорировать примыкающую к нему вершину, чтобы на каждой стороне вспомогательного пути вы получали только те вершины, которые не являются частью вспомогательного пути.