Минимальное покрытие пути в ориентированном ациклическом графе
Вопрос, который я собираюсь здесь задать, уже задавался ранее при переполнении стека. Но я не могу правильно понять решения, опубликованные Скиминок.
Вот ссылка.
Я попробовал решение, опубликованное по вышеуказанной ссылке, с двумя примерами тестов, но не смог получить правильный ответ.
Для теста 1::
N = 3 и K = 2
5 4 7
DAG будет::
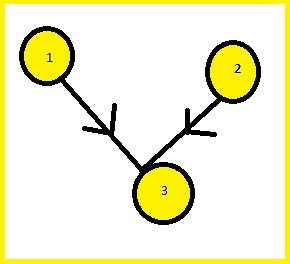
Примечание: я построил вышеупомянутую DAG, учитывая:
Пусть pi и pj - две разные проблемы. Затем мы нарисуем направленное ребро от pi до pj тогда и только тогда, когда pj может быть решен сразу после pi в тот же день, последовательно. А именно, должны быть выполнены следующие условия:
я |vi - vj| >= K (требование к рейтингу). Затем я построил двудольный граф с учетом: Для каждого направленного ребра (u, v) исходного DAG следует добавить неориентированный ребро (au, bv) к двудольному графу, где {ai} и {bi} - две части размера n. Ответ = максимальное совпадение мощности в приведенном выше двудольном графе. максимальное совпадение мощности в приведенном выше двудольном графе =1 (egde зеленого цвета) Но ответ 2. Аналогично, пример теста 2: 5 1 5 3 4 5 6 Максимальное количество элементов в приведенном выше графике - БОЛЬШЕ, ЧЕМ ОДИН, но Правильный ответ - 1. Я думаю, что я не реализую это правильно, пожалуйста, вы можете сказать, где я делаю ошибку или есть какой-либо другой метод Спасибо!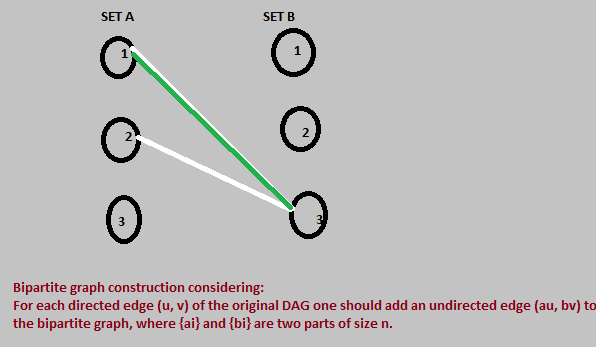
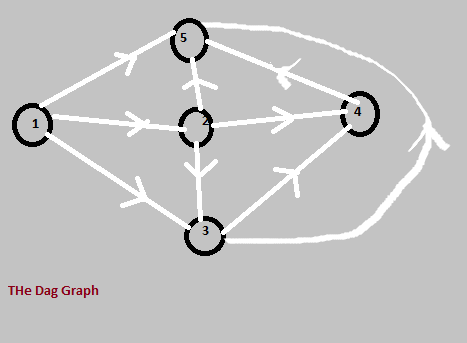
1 ответ
Я нашел ответ сам, на следующий день я отправил этот вопрос.
И мое решение прошло все тестовые случаи.
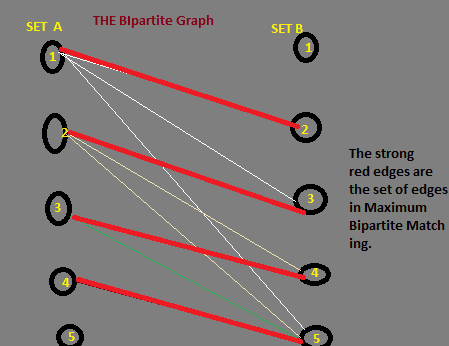
Я делал ошибку на последнем этапе. На самом деле ответ / решение - это общее количество вершин в SET B, которое не содержит ребра максимального двойного соответствия.
Например, на примере тестового примера 1::
Максимальное совпадение M={(1A,3B)}.
Ни одно ребро максимального совпадения не попадает на две вершины (вершина 1 и вершина 2). Поэтому ответ равен числу таких вершин =2
Для теста 2::
Максимальное совпадение M={(1A,2B),(2A,3B),(3A,4B),(4A,5B)}.
Ни одно ребро максимального соответствия не попадает в одну вершину (вершина 1). Так что ответ равен 1