Каков наилучший алгоритм проверки, является ли число простым?
Просто пример того, что я ищу: я мог бы представить каждое нечетное число с битом, например, для данного диапазона чисел (1, 10], начиная с 3:
1110
Следующий словарь можно сжать более правильно? Я мог бы определить кратные пять с некоторой работой, но числа, заканчивающиеся на 1, 3, 7 или 9, должны быть там в массиве битов. Надеюсь, это прояснит, чего я хочу.
Я ищу лучший алгоритм, чтобы проверить, является ли число простым, то есть булевой функцией:
bool isprime(number);
Я хотел бы знать лучший алгоритм для реализации этой функциональности. Естественно, была бы структура данных, которую я мог бы запросить. Я определяю лучший алгоритм, который будет алгоритмом, который создает структуру данных с самым низким потреблением памяти для диапазона (1, N], где N - константа.
35 ответов
Есть много способов сделать тест на первичность.
На самом деле нет структуры данных для запроса. Если у вас есть много чисел для тестирования, вам, вероятно, следует выполнить вероятностный тест, поскольку они быстрее, а затем выполнить детерминистический тест, чтобы убедиться, что число простое.
Вы должны знать, что математика позади самых быстрых алгоритмов не для слабонервных.
Самым быстрым алгоритмом для общего простого тестирования является AKS. Статья в Википедии подробно описывает это и ссылается на оригинальную статью.
Если вы хотите найти большие числа, посмотрите на простые числа, которые имеют специальные формы, такие как простые числа Мерсенна.
Алгоритм, который я обычно реализую (легко понять и кодировать), выглядит следующим образом (на Python):
def isprime(n):
"""Returns True if n is prime."""
if n == 2:
return True
if n == 3:
return True
if n % 2 == 0:
return False
if n % 3 == 0:
return False
i = 5
w = 2
while i * i <= n:
if n % i == 0:
return False
i += w
w = 6 - w
return True
Это вариант классики O(sqrt(N)) алгоритм. Он использует тот факт, что простое число (кроме 2 и 3) имеет форму 6k - 1 или же 6k + 1 и смотрит только на делители этой формы.
Иногда, если мне действительно нужна скорость и диапазон ограничен, я применяю тест псевдопростого числа на основе маленькой теоремы Ферма. Если мне действительно нужно больше скорости (т.е. вообще избегать алгоритма O(sqrt(N))), я предварительно вычисляю ложные срабатывания (см. Числа Кармайкла) и выполняю двоичный поиск. Это, безусловно, самый быстрый тест, который я когда-либо проводил, единственным недостатком является то, что диапазон ограничен.
На мой взгляд, лучший способ - использовать то, что было раньше.
Есть списки первых N простые числа в интернете с N протяженностью не менее пятидесяти миллионов. Загрузите файлы и используйте их, это, вероятно, будет намного быстрее, чем любой другой метод, который вы придумали.
Если вам нужен реальный алгоритм для создания собственных простых чисел, в Википедии есть много полезных вещей о простых числах, в том числе ссылки на различные методы для этого и простое тестирование здесь, как основанные на вероятности, так и быстрые детерминированные методы.
Должны быть согласованные усилия, чтобы найти первый миллиард (или даже больше) простых чисел и опубликовать их где-нибудь в сети, чтобы люди могли перестать выполнять эту работу снова и снова и снова и...:-)
bool isPrime(int n)
{
// Corner cases
if (n <= 1) return false;
if (n <= 3) return true;
// This is checked so that we can skip
// middle five numbers in below loop
if (n%2 == 0 || n%3 == 0) return false;
for (int i=5; i*i<=n; i=i+6)
if (n%i == 0 || n%(i+2) == 0)
return false;
return true;
}
this is just c++ implementation of above AKS algorithm
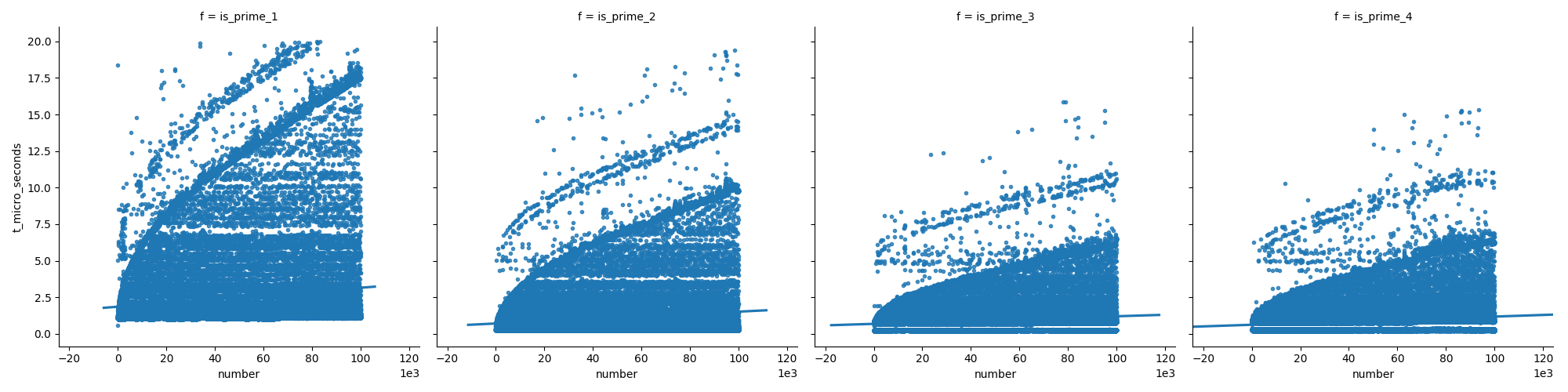
Я сравнил эффективность самых популярных предложений, чтобы определить, является ли число простым. я использовал python 3.6 на ubuntu 17.10; Я проверил с номерами до 100.000 (вы можете проверить с большими числами, используя мой код ниже).
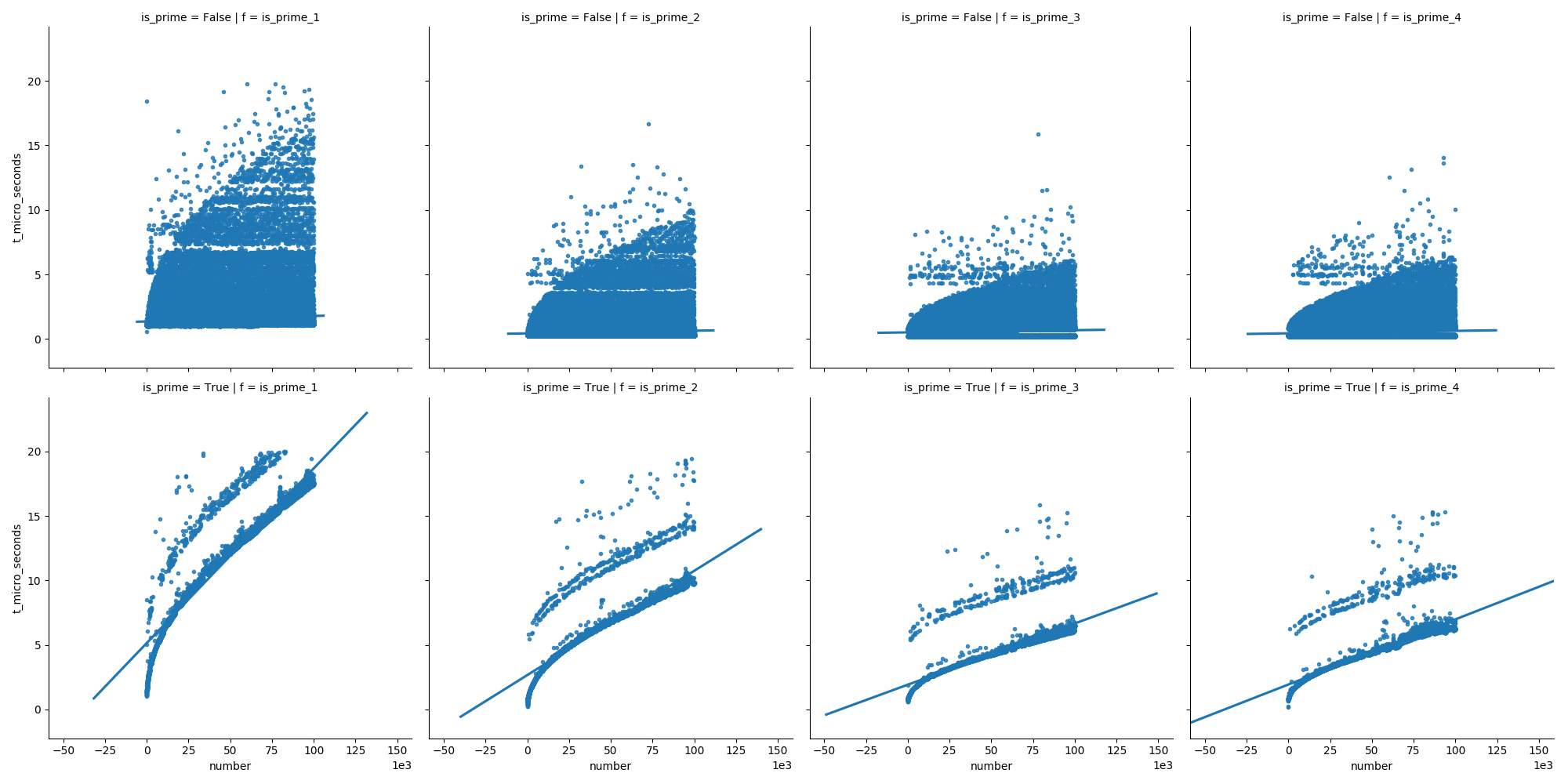
На этом первом графике сравниваются функции (которые объясняются ниже в моем ответе), показывая, что последние функции не растут так же быстро, как первая при увеличении чисел.
И на втором графике мы видим, что в случае простых чисел время неуклонно растет, но не простые числа растут не так быстро во времени (потому что большинство из них можно устранить на ранней стадии).
Вот функции, которые я использовал:
этот ответ и этот ответ предложил конструкцию, использующую
all():def is_prime_1(n): return n > 1 and all(n % i for i in range(2, int(math.sqrt(n)) + 1))Этот ответ использовал какой-то цикл while:
def is_prime_2(n): if n <= 1: return False if n == 2: return True if n == 3: return True if n % 2 == 0: return False if n % 3 == 0: return False i = 5 w = 2 while i * i <= n: if n % i == 0: return False i += w w = 6 - w return TrueЭтот ответ включал версию с
forцикл:def is_prime_3(n): if n <= 1: return False if n % 2 == 0 and n > 2: return False for i in range(3, int(math.sqrt(n)) + 1, 2): if n % i == 0: return False return TrueИ я смешал несколько идей из других ответов в новый:
def is_prime_4(n): if n <= 1: # negative numbers, 0 or 1 return False if n <= 3: # 2 and 3 return True if n % 2 == 0 or n % 3 == 0: return False for i in range(5, int(math.sqrt(n)) + 1, 2): if n % i == 0: return False return True
Вот мой скрипт для сравнения вариантов:
import math
import pandas as pd
import seaborn as sns
import time
from matplotlib import pyplot as plt
def is_prime_1(n):
...
def is_prime_2(n):
...
def is_prime_3(n):
...
def is_prime_4(n):
...
default_func_list = (is_prime_1, is_prime_2, is_prime_3, is_prime_4)
def assert_equal_results(func_list=default_func_list, n):
for i in range(-2, n):
r_list = [f(i) for f in func_list]
if not all(r == r_list[0] for r in r_list):
print(i, r_list)
raise ValueError
print('all functions return the same results for integers up to {}'.format(n))
def compare_functions(func_list=default_func_list, n):
result_list = []
n_measurements = 3
for f in func_list:
for i in range(1, n + 1):
ret_list = []
t_sum = 0
for _ in range(n_measurements):
t_start = time.perf_counter()
is_prime = f(i)
t_end = time.perf_counter()
ret_list.append(is_prime)
t_sum += (t_end - t_start)
is_prime = ret_list[0]
assert all(ret == is_prime for ret in ret_list)
result_list.append((f.__name__, i, is_prime, t_sum / n_measurements))
df = pd.DataFrame(
data=result_list,
columns=['f', 'number', 'is_prime', 't_seconds'])
df['t_micro_seconds'] = df['t_seconds'].map(lambda x: round(x * 10**6, 2))
print('df.shape:', df.shape)
print()
print('', '-' * 41)
print('| {:11s} | {:11s} | {:11s} |'.format(
'is_prime', 'count', 'percent'))
df_sub1 = df[df['f'] == 'is_prime_1']
print('| {:11s} | {:11,d} | {:9.1f} % |'.format(
'all', df_sub1.shape[0], 100))
for (is_prime, count) in df_sub1['is_prime'].value_counts().iteritems():
print('| {:11s} | {:11,d} | {:9.1f} % |'.format(
str(is_prime), count, count * 100 / df_sub1.shape[0]))
print('', '-' * 41)
print()
print('', '-' * 69)
print('| {:11s} | {:11s} | {:11s} | {:11s} | {:11s} |'.format(
'f', 'is_prime', 't min (us)', 't mean (us)', 't max (us)'))
for f, df_sub1 in df.groupby(['f', ]):
col = df_sub1['t_micro_seconds']
print('|{0}|{0}|{0}|{0}|{0}|'.format('-' * 13))
print('| {:11s} | {:11s} | {:11.2f} | {:11.2f} | {:11.2f} |'.format(
f, 'all', col.min(), col.mean(), col.max()))
for is_prime, df_sub2 in df_sub1.groupby(['is_prime', ]):
col = df_sub2['t_micro_seconds']
print('| {:11s} | {:11s} | {:11.2f} | {:11.2f} | {:11.2f} |'.format(
f, str(is_prime), col.min(), col.mean(), col.max()))
print('', '-' * 69)
return df
Запуск функции compare_functions(n=10**5) (числа до 100.000) я получаю этот вывод:
df.shape: (400000, 5)
-----------------------------------------
| is_prime | count | percent |
| all | 100,000 | 100.0 % |
| False | 90,408 | 90.4 % |
| True | 9,592 | 9.6 % |
-----------------------------------------
---------------------------------------------------------------------
| f | is_prime | t min (us) | t mean (us) | t max (us) |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_1 | all | 0.57 | 2.50 | 154.35 |
| is_prime_1 | False | 0.57 | 1.52 | 154.35 |
| is_prime_1 | True | 0.89 | 11.66 | 55.54 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_2 | all | 0.24 | 1.14 | 304.82 |
| is_prime_2 | False | 0.24 | 0.56 | 304.82 |
| is_prime_2 | True | 0.25 | 6.67 | 48.49 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_3 | all | 0.20 | 0.95 | 50.99 |
| is_prime_3 | False | 0.20 | 0.60 | 40.62 |
| is_prime_3 | True | 0.58 | 4.22 | 50.99 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_4 | all | 0.20 | 0.89 | 20.09 |
| is_prime_4 | False | 0.21 | 0.53 | 14.63 |
| is_prime_4 | True | 0.20 | 4.27 | 20.09 |
---------------------------------------------------------------------
Затем, запустив функцию compare_functions(n=10**6) (числа до 1.000.000) я получаю этот вывод:
df.shape: (4000000, 5)
-----------------------------------------
| is_prime | count | percent |
| all | 1,000,000 | 100.0 % |
| False | 921,502 | 92.2 % |
| True | 78,498 | 7.8 % |
-----------------------------------------
---------------------------------------------------------------------
| f | is_prime | t min (us) | t mean (us) | t max (us) |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_1 | all | 0.51 | 5.39 | 1414.87 |
| is_prime_1 | False | 0.51 | 2.19 | 413.42 |
| is_prime_1 | True | 0.87 | 42.98 | 1414.87 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_2 | all | 0.24 | 2.65 | 612.69 |
| is_prime_2 | False | 0.24 | 0.89 | 322.81 |
| is_prime_2 | True | 0.24 | 23.27 | 612.69 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_3 | all | 0.20 | 1.93 | 67.40 |
| is_prime_3 | False | 0.20 | 0.82 | 61.39 |
| is_prime_3 | True | 0.59 | 14.97 | 67.40 |
|-------------|-------------|-------------|-------------|-------------|
| is_prime_4 | all | 0.18 | 1.88 | 332.13 |
| is_prime_4 | False | 0.20 | 0.74 | 311.94 |
| is_prime_4 | True | 0.18 | 15.23 | 332.13 |
---------------------------------------------------------------------
Я использовал следующий скрипт для отображения результатов:
def plot_1(func_list=default_func_list, n):
df_orig = compare_functions(func_list=func_list, n=n)
df_filtered = df_orig[df_orig['t_micro_seconds'] <= 20]
sns.lmplot(
data=df_filtered, x='number', y='t_micro_seconds',
col='f',
# row='is_prime',
markers='.',
ci=None)
plt.ticklabel_format(style='sci', axis='x', scilimits=(3, 3))
plt.show()
Можно использовать sympy.
import sympy
sympy.ntheory.primetest.isprime(33393939393929292929292911111111)
True
Из симпати документов. Первым шагом является поиск тривиальных факторов, которые в случае их обнаружения позволяют быстро вернуться. Далее, если сито достаточно велико, используйте поиск сито на сите. Для небольших чисел выполняется ряд детерминированных тестов Миллера-Рабина с основаниями, о которых известно, что в их диапазоне нет контрпримеров. Наконец, если число больше 2^64, выполняется сильный тест BPSW. Несмотря на то, что это вероятный простой тест, и мы считаем, что существуют контрпримеры, известных контрпримеров нет
Согласно википедии, Сито Эратосфена имеет сложность O(n * (log n) * (log log n)) и требует O(n) память - так что это хорошее начало, если вы не тестируете особо большие числа.
В Python 3:
def is_prime(a):
if a < 2:
return False
elif a!=2 and a % 2 == 0:
return False
else:
return all (a % i for i in range(3, int(a**0.5)+1))
Пояснение: Простое число - это число, которое делится только на себя и 1. Пример: 2,3,5,7...
1) если a<2: если "a" меньше 2, это не простое число.
2) elif a! = 2 и a % 2 == 0: если "a" делится на 2, то это определенно не простое число. Но если a=2, мы не хотим оценивать это, поскольку это простое число. Отсюда условие а! = 2
3) вернуть все (% i для i в диапазоне (3, int (a0.5) +1)): ** Сначала посмотрите, что команда all() делает в python. Начиная с 3 мы делим "а" до его квадратного корня (а **0,5). Если "а" делится, вывод будет ложным. Почему квадратный корень? Допустим, а =16. Квадратный корень из 16 = 4. Нам не нужно оценивать до 15. Нам нужно только проверить до 4, чтобы сказать, что это не простое число.
Дополнительно: цикл для нахождения всех простых чисел в диапазоне.
for i in range(1,100):
if is_prime(i):
print("{} is a prime number".format(i))
Для больших чисел вы не можете просто наивно проверить, делится ли число кандидатов N на одно из чисел меньше, чем sqrt(N). Доступны гораздо более масштабируемые тесты, такие как тест примитивности Миллера-Рабина. Ниже у вас есть реализация в Python:
def is_prime(x):
"""Fast implementation fo Miller-Rabin primality test, guaranteed to be correct."""
import math
def get_sd(x):
"""Returns (s: int, d: int) for which x = d*2^s """
if not x: return 0, 0
s = 0
while 1:
if x % 2 == 0:
x /= 2
s += 1
else:
return s, x
if x <= 2:
return x == 2
# x - 1 = d*2^s
s, d = get_sd(x - 1)
if not s:
return False # divisible by 2!
log2x = int(math.log(x) / math.log(2)) + 1
# As long as Riemann hypothesis holds true, it is impossible
# that all the numbers below this threshold are strong liars.
# Hence the number is guaranteed to be a prime if no contradiction is found.
threshold = min(x, 2*log2x*log2x+1)
for a in range(2, threshold):
# From Fermat's little theorem if x is a prime then a^(x-1) % x == 1
# Hence the below must hold true if x is indeed a prime:
if pow(a, d, x) != 1:
for r in range(0, s):
if -pow(a, d*2**r, x) % x == 1:
break
else:
# Contradicts Fermat's little theorem, hence not a prime.
return False
# No contradiction found, hence x must be a prime.
return True
Вы можете использовать его, чтобы найти огромные простые числа:
x = 10000000000000000000000000000000000000000000000000000000000000000000000000000
for e in range(1000):
if is_prime(x + e):
print('%d is a prime!' % (x + e))
break
# 10000000000000000000000000000000000000000000000000000000000000000000000000133 is a prime!
Если вы тестируете случайные целые числа, возможно, вы хотите сначала проверить, делится ли число кандидатов на любое из простых чисел, меньших, скажем, 1000, прежде чем позвонить Миллеру-Рабину. Это поможет вам отфильтровать очевидные не простые числа, такие как 10444344345.
Python 3:
def is_prime(a):
return a > 1 and all(a % i for i in range(2, int(a**0.5) + 1))
Слишком поздно на вечеринку, но надеюсь, это поможет. Это актуально, если вы ищете большие простые числа:
Для проверки больших нечетных чисел необходимо использовать тест Ферма и / или Миллера-Рабина.
Эти тесты используют модульное возведение в степень, которое является довольно дорогим, для n биты возведения в степень вам нужно как минимум n большое умножение и инт n большой международный отдел. Это означает, что сложность модульного возведения в степень составляет O(n³).
Поэтому, прежде чем использовать большие пушки, вам нужно сделать несколько пробных делений. Но не делайте это наивно, есть способ сделать это быстро. Сначала умножьте столько простых чисел, сколько вписывается в слова, которые вы используете для больших целых чисел. Если вы используете 32-битные слова, умножьте 3*5*7*11*13*17*19*23*29=3234846615 и вычислите наибольший общий делитель с числом, которое вы тестируете, используя евклидов алгоритм. После первого шага число уменьшается ниже размера слова и продолжается алгоритм, не выполняя полных целочисленных делений. Если GCD!= 1, это означает, что одно из простых чисел, которые вы умножили вместе, делит число, поэтому у вас есть доказательство того, что оно не простое. Затем продолжите с 31*37*41*43*47 = 95041567 и так далее.
После того, как вы проверили несколько сотен (или тысяч) простых чисел таким образом, вы можете выполнить 40 раундов теста Миллера-Рабина, чтобы подтвердить, что число простое, после 40 раундов вы можете быть уверены, что число простое, есть только 2^-80 шанс, что это нет (это скорее ваши аппаратные неисправности...).
Лучший алгоритм для простого числа javascript
function isPrime(num) {
if (num <= 1) return false;
else if (num <= 3) return true;
else if (num % 2 == 0 || num % 3 == 0) return false;
var i = 5;
while (i * i <= num) {
if (num % i == 0 || num % (i + 2) == 0) return false;
i += 6;
}
return true
}
import math
import time
def check_prime(n):
if n == 1:
return False
if n == 2:
return True
if n % 2 == 0:
return False
from_i = 3
to_i = math.sqrt(n) + 1
for i in range(from_i, int(to_i), 2):
if n % i == 0:
return False
return True
В Python:
def is_prime(n):
return not any(n % p == 0 for p in range(2, int(math.sqrt(n)) + 1))
Более прямое преобразование из математического формализма в Python будет использовать все (n% p! = 0...), но это требует строгой оценки всех значений p. Не любая версия может завершиться досрочно, если найдено значение True.
У меня есть простая функция, которая работает до (2^61)-1 Здесь:
from math import sqrt
def isprime(num): num > 1 and return all(num % x for x in range(2, int(sqrt(num)+1)))
Объяснение:
all() Функция может быть переопределена следующим образом:
def all(variables):
for element in variables:
if not element: return False
return True
all() Функция просто проходит через серию bools / numbers и возвращает False если он видит 0 или False,
sqrt() Функция просто делает квадратный корень из числа.
Например:
>>> from math import sqrt
>>> sqrt(9)
>>> 3
>>> sqrt(100)
>>> 10
num % x part возвращает остаток от num / x.
В заключение, range(2, int(sqrt(num))) означает, что он создаст список, который начинается в 2 и заканчивается в int(sqrt(num)+1)
Для получения дополнительной информации о ассортименте, посмотрите на этот сайт!
num > 1 часть просто проверяет, является ли переменная num больше 1, потому что 1 и 0 не считаются простыми числами.
Я надеюсь, что это помогло:)
bool isPrime(int n) {
if(n <= 3)
return (n > 1)==0? false: true;
else if(n%2 == 0 || n%3 == 0)
return false;
int i = 5;
while(i * i <= n){
if(n%i == 0 || (n%(i+2) == 0))
return false;
i = i + 6;
}
return true;
}
для любого числа минимальное количество итераций для проверки того, является ли число простым или нет, может составлять от 2 до квадратного корня из числа. Чтобы еще больше сократить количество итераций, мы можем проверить, делится ли число на 2 или 3, поскольку максимальное число можно исключить, проверив, делится ли число на 2 или 3. Кроме того, любое простое число больше 3 может быть выражено как 6k+1 или 6к-1. Таким образом, итерация может идти от 6k+1 до квадратного корня из числа.
Позвольте предложить вам идеальное решение для 64-битных целых чисел. Извините за использование C#. Вы еще не указали его как python в своем первом посте. Надеюсь, вы сможете найти простую функцию modPow и легко ее проанализировать.
public static bool IsPrime(ulong number)
{
return number == 2
? true
: (BigInterger.ModPow(2, number, number) == 2
? (number & 1 != 0 && BinarySearchInA001567(number) == false)
: false)
}
public static bool BinarySearchInA001567(ulong number)
{
// Is number in list?
// todo: Binary Search in A001567 (https://oeis.org/A001567) below 2 ^ 64
// Only 2.35 Gigabytes as a text file http://www.cecm.sfu.ca/Pseudoprimes/index-2-to-64.html
}
Простое число - это любое число, которое делится только на 1 и само себя. Все остальные числа называются составными.
Самый простой способ найти простое число - проверить, является ли введенное число составным числом:
function isPrime(number) {
// Check if a number is composite
for (let i = 2; i < number; i++) {
if (number % i === 0) {
return false;
}
}
// Return true for prime numbers
return true;
}
Программа должна разделить стоимость numberна все целые числа от 1 до его значения. Если это число можно разделить поровну не только на единицу, но и само по себе это составное число.
Начальное значение переменной i должно быть 2, потому что как простые, так и составные числа могут делиться на 1 без остатка.
for (let i = 2; i < number; i++)
потом i меньше чем numberпо той же причине. И простые, и составные числа могут делиться сами по себе поровну. Поэтому нет причин проверять это.
Затем мы проверяем, можно ли разделить переменную равномерно, используя оператор остатка.
if (number % i === 0) {
return false;
}
Если остаток равен нулю, это означает, что number может быть разделено поровну, следовательно, является составным числом и возвращает false.
Если введенное число не соответствует условию, это означает, что это простое число, и функция возвращает истину.
myInp=int(input("Enter a number: "))
if myInp==1:
print("The number {} is neither a prime not composite no".format(myInp))
elif myInp>1:
for i in range(2,myInp//2+1):
if myInp%i==0:
print("The Number {} is not a prime no".format(myInp))
print("Because",i,"times",myInp//i,"is",myInp)
break
else:
print("The Number {} is a prime no".format(myInp))
else:
print("Alas the no {} is a not a prime no".format(myInp))
Вот мой взгляд на ответ:
def isprime(num):
return num <= 3 or (num + 1) % 6 == 0 or (num - 1) % 6 == 0
Функция вернет True, если какое-либо из свойств ниже - True. Эти свойства математически определяют, что такое простое число.
- Число меньше или равно 3
- Число + 1 делится на 6
- Число - 1 делится на 6
public static boolean isPrime(int number) {
if(number < 2)
return false;
else if(number == 2 || number == 3)
return true;
else {
for(int i=2;i<=number/2;i++)
if(number%i == 0)
return false;
else if(i==number/2)
return true;
}
return false;
}
from math import isqrt
def is_prime(n: int) -> bool:
if n <= 3:
return n > 1
if n % 2 == 0 or n % 3 == 0:
return False
limit = isqrt(n)
for i in range(5, limit+1, 6):
if n % i == 0 or n % (i+2) == 0:
return False
return True
Метод пробного деления.
ЛУЧШЕЕ РЕШЕНИЕ
Я не уверен, понимаю ли я концепцию
Time complexity: O(sqrt(n))а такжеSpace complexity: O(1)в этом контексте, но функцияprime(n)вероятно,fastest way (least iterations)вычислить, является ли число простым числом любого размера.
Это, вероятно, ЛУЧШЕЕ решение в Интернете на сегодняшний день, 11 марта 2022 года. Отзывы и использование приветствуются.
Этот же код можно применять на любых языках, таких как C, C++, Go Lang,Java, .NET, Python, Rust и т. д., с той же логикой и преимуществами в производительности. Это довольно быстро. Я не видел, чтобы это было реализовано раньше, и это было сделано изначально.
Если вы смотрите на скорость и производительность, вот
"""BEST"""обнадеживающее решение, которое я могу дать:
Максимальное количество итераций 16 666 для n == 100 000 вместо 100 000, как обычно.
Коды также можно найти здесь: https://github.com/ganeshkbhat/fastprimecalculations
Если вы используете его для своего проекта, пожалуйста, потратьте 2 минуты своего времени, сообщив мне об этом, отправив мне электронное письмо или зарегистрировав проблему Github с заголовком темы.
[User], или же
starмой проект на гитхабе. Но дайте мне знать здесь https://github.com/ganeshkbhat/fastprimecalculations . Я хотел бы знать поклонников и пользователей логики кода
def prime(n):
if ((n == 2 or n == 3 or n == 5 or n == 7)):
return True
if (n == 1 or ((n > 7) and (n % 5 == 0 or n % 7 == 0 or n % 2 == 0 or n % 3 == 0))):
return False
if ( type((n - 1) / 6) == int or type((n + 1) / 6) == int):
for i in range(1, n):
factorsix = (i * 6)
five = n / (5 + factorsix)
seven = n / (7 + factorsix)
if ( ((five > 1) and type(five) == int) or ((seven > 1) and type(five) == int) ):
return False;
if (factorsix > n):
break;
return True
return False
Вот разбор всех способов расчета:
Обычный способ проверки на простоту:
def isPrimeConventionalWay(n):
count = 0
if (n <= 1):
return False;
# Check from 2 to n-1
# Max iterations 99998 for n == 100000
for i in range(2,n):
# Counting Iterations
count += 1
if (n % i == 0):
print("count: Prime Conventional way", count)
return False;
print("count: Prime Conventional way", count)
return True;
SQUAREROOT способ проверки на простоту:
def isPrimeSquarerootWay(num):
count = 0
# if not is_number num return False
if (num < 2):
print("count: Prime Squareroot way", count)
return False
s = math.sqrt(num)
for i in range(2, num):
# Counting Iterations
count += 1
if (num % i == 0):
print("count: Prime Squareroot way", count)
return False
print("count: Prime Squareroot way", count)
return True
ДРУГИЕ СПОСОБЫ:
def isprimeAKSWay(n):
"""Returns True if n is prime."""
count = 0
if n == 2:
return True
if n == 3:
return True
if n % 2 == 0:
return False
if n % 3 == 0:
return False
i = 5
w = 2
while i * i <= n:
count += 1
if n % i == 0:
print("count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way", count)
return False
i += w
w = 6 - w
print("count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way", count)
return True
ПРЕДЛАГАЕМЫЙ способ проверки на простоту:
def prime(n):
count = 0
if ((n == 2 or n == 3 or n == 5 or n == 7)):
print("count: Prime Unconventional way", count)
return True
if (n == 1 or ((n > 7) and (n % 5 == 0 or n % 7 == 0 or n % 2 == 0 or n % 3 == 0))):
print("count: Prime Unconventional way", count)
return False
if (((n - 1) / 6).is_integer()) or (((n + 1) / 6).is_integer()):
for i in range(1, n):
# Counting Iterations
count += 1
five = 5 + (i * 6)
seven = 7 + (i * 6)
if ((((n / five) > 1) and (n / five).is_integer()) or (((n / seven) > 1) and ((n / seven).is_integer()))):
print("count: Prime Unconventional way", count)
return False;
if ((i * 6) > n):
# Max iterations 16666 for n == 100000 instead of 100000
break;
print("count: Prime Unconventional way", count)
return True
print("count: Prime Unconventional way", count)
return False
Тесты для сравнения с традиционным способом проверки простых чисел.
def test_primecalculations():
count = 0
iterations = 100000
arr = []
for i in range(1, iterations):
traditional = isPrimeConventionalWay(i)
newer = prime(i)
if (traditional == newer):
count = count + 1
else:
arr.push([traditional, newer, i])
print("[count, iterations, arr] list: ", count, iterations, arr)
if (count == iterations):
return True
return False
# print("Tests Passed: ", test_primecalculations())
Вы увидите результаты подсчета количества итераций, как показано ниже для
check of prime number: 100007:
print("Is Prime 100007: ", isPrimeConventionalWay(100007))
print("Is Prime 100007: ", isPrimeSquarerootWay(100007))
print("Is Prime 100007: ", prime(100007))
print("Is Prime 100007: ", isprimeAKSWay(100007))
count: Prime Conventional way 96
Is Prime 100007: False
count: Prime Squareroot way 96
Is Prime 100007: False
count: Prime Unconventional way 15
Is Prime 100007: False
count: Prime AKS - Mersenne primes - Fermat's little theorem or whatever way 32
Is Prime 100007: False
Ниже приведены некоторые тесты производительности и результаты:
import time
isPrimeConventionalWayArr = []
isPrimeSquarerootWayArr = []
primeArr = []
isprimeAKSWayArr = []
def tests_performance_isPrimeConventionalWayArr():
global isPrimeConventionalWayArr
for i in range(1, 1000000):
start = time.perf_counter_ns()
isPrimeConventionalWay(30000239)
end = time.perf_counter_ns()
isPrimeConventionalWayArr.append(end - start)
tests_performance_isPrimeConventionalWayArr()
def tests_performance_isPrimeSquarerootWayArr():
global isPrimeSquarerootWayArr
for i in range(1, 1000000):
start = time.perf_counter_ns()
isPrimeSquarerootWay(30000239)
end = time.perf_counter_ns()
isPrimeSquarerootWayArr.append(end - start)
tests_performance_isPrimeSquarerootWayArr()
def tests_performance_primeArr():
global primeArr
for i in range(1, 1000000):
start = time.perf_counter_ns()
prime(30000239)
end = time.perf_counter_ns()
primeArr.append(end - start)
tests_performance_primeArr()
def tests_performance_isprimeAKSWayArr():
global isprimeAKSWayArr
for i in range(1, 1000000):
start = time.perf_counter_ns()
isprimeAKSWay(30000239)
end = time.perf_counter_ns()
isprimeAKSWayArr.append(end - start)
tests_performance_isprimeAKSWayArr()
print("isPrimeConventionalWayArr: ", sum(isPrimeConventionalWayArr)/len(isPrimeConventionalWayArr))
print("isPrimeSquarerootWayArr: ", sum(isPrimeSquarerootWayArr)/len(isPrimeSquarerootWayArr))
print("primeArr: ", sum(primeArr)/len(primeArr))
print("isprimeAKSWayArr: ", sum(isprimeAKSWayArr)/len(isprimeAKSWayArr))
Образец 1 миллион итераций
Итерация 1:
isPrimeConventionalWayArr: 1749.97224997225
isPrimeSquarerootWayArr: 1835.6258356258356
primeArr (suggested): 475.2365752365752
isprimeAKSWayArr: 1177.982377982378
Итерация 2:
isPrimeConventionalWayArr: 1803.141403141403
isPrimeSquarerootWayArr: 2184.222484222484
primeArr (suggested): 572.6434726434726
isprimeAKSWayArr: 1403.3838033838033
Итерация 3:
isPrimeConventionalWayArr: 1876.941976941977
isPrimeSquarerootWayArr: 2190.43299043299
primeArr (suggested): 569.7365697365698
isprimeAKSWayArr: 1449.4147494147494
Итерация 4:
isPrimeConventionalWayArr: 1873.2779732779734
isPrimeSquarerootWayArr: 2177.154777154777
primeArr (suggested): 590.4243904243905
isprimeAKSWayArr: 1401.9143019143019
Итерация 5:
isPrimeConventionalWayArr: 1891.1986911986912
isPrimeSquarerootWayArr: 2218.093218093218
primeArr (suggested): 571.6938716938716
isprimeAKSWayArr: 1397.6471976471976
Итерация 6:
isPrimeConventionalWayArr: 1868.8454688454688
isPrimeSquarerootWayArr: 2168.034368034368
primeArr (suggested): 566.3278663278663
isprimeAKSWayArr: 1393.090193090193
Итерация 7:
isPrimeConventionalWayArr: 1879.4764794764794
isPrimeSquarerootWayArr: 2199.030199030199
primeArr (suggested): 574.055874055874
isprimeAKSWayArr: 1397.7587977587978
Итерация 8:
isPrimeConventionalWayArr: 1789.2868892868894
isPrimeSquarerootWayArr: 2182.3258823258825
primeArr (suggested): 569.3206693206694
isprimeAKSWayArr: 1407.1486071486072
Чтобы узнать, является ли число или числа в диапазоне простыми.
#!usr/bin/python3
def prime_check(*args):
for arg in args:
if arg > 1: # prime numbers are greater than 1
for i in range(2,arg): # check for factors
if(arg % i) == 0:
print(arg,"is not Prime")
print(i,"times",arg//i,"is",arg)
break
else:
print(arg,"is Prime")
# if input number is less than
# or equal to 1, it is not prime
else:
print(arg,"is not Prime")
return
# Calling Now
prime_check(*list(range(101))) # This will check all the numbers in range 0 to 100
prime_check(#anynumber) # Put any number while calling it will check.
### is_prime(number) =
### if number % p1 !=0 for all p1(prime numbers) < (sqrt(number) + 1),
### filter numbers that are not prime from divisors
import math
def check_prime(N, prime_numbers_found = [2]):
if int(math.sqrt(N)) + 1 >= prime_numbers_found[-1]:
divisor_range = range(2, int(math.sqrt(N)) + 1)
else:
divisor_range = prime_numbers_found
for number in divisor_range:
if number not in prime_numbers_found:
if check_prime(number, prime_numbers_found):
prime_numbers_found.append(number)
if N % number == 0:
return False
else:
if N % number == 0:
return False
return True
Я думаю, что одним из самых быстрых является мой метод, который я сделал.
void prime(long long int number) {
// Establishing Variables
long long int i = 5;
int w = 2;
const long long int lim = sqrt(number);
// Gets 2 and 3 out of the way
if (number == 1) { cout << number << " is hard to classify. \n"; return; }
if (number == 2) { cout << number << " is Prime. \n"; return; }
if (number == 3) { cout << number << " is Prime. \n"; return; }
// Tests Odd Ball Factors
if (number % 2 == 0) { cout << number << " is not Prime. \n"; return; }
if (number % 3 == 0) { cout << number << " is not Prime. \n"; return; }
while (i <= lim) {
if (number % i == 0) { cout << number << " is not Prime. \n"; return; }
// Tests Number
i = i + w; // Increments number
w = 6 - i; // We already tested 2 and 3
// So this removes testing multepules of this
}
cout << number << " is Prime. \n"; return;
}
Мы можем использовать потоки Java для реализации этого в O(sqrt(n)); Учтите, что noneMatch - это метод shortCircuiting, который останавливает операцию, когда считает ее ненужной для определения результата:
Scanner in = new Scanner(System.in);
int n = in.nextInt();
System.out.println(n == 2 ? "Prime" : IntStream.rangeClosed(2, ((int)(Math.sqrt(n)) + 1)).noneMatch(a -> n % a == 0) ? "Prime" : "Not Prime");
Схожая идея с алгоритмом AKS, о котором упоминалось
public static boolean isPrime(int n) {
if(n == 2 || n == 3) return true;
if((n & 1 ) == 0 || n % 3 == 0) return false;
int limit = (int)Math.sqrt(n) + 1;
for(int i = 5, w = 2; i <= limit; i += w, w = 6 - w) {
if(n % i == 0) return false;
numChecks++;
}
return true;
}
Наименьшая память? Это не маленький, но шаг в правильном направлении.
class PrimeDictionary {
BitArray bits;
public PrimeDictionary(int n) {
bits = new BitArray(n + 1);
for (int i = 0; 2 * i + 3 <= n; i++) {
bits.Set(i, CheckPrimality(2 * i + 3));
}
}
public PrimeDictionary(IEnumerable<int> primes) {
bits = new BitArray(primes.Max());
foreach(var prime in primes.Where(p => p != 2)) {
bits.Set((prime - 3) / 2, true);
}
}
public bool IsPrime(int k) {
if (k == 2) {
return true;
}
if (k % 2 == 0) {
return false;
}
return bits[(k - 3) / 2];
}
}
Конечно, вы должны указать определение CheckPrimality,
Вы можете попробовать что-то вроде этого.
def main():
try:
user_in = int(input("Enter a number to determine whether the number is prime or not: "))
except ValueError:
print()
print("You must enter a number!")
print()
return
list_range = list(range(2,user_in+1))
divisor_list = []
for number in list_range:
if user_in%number==0:
divisor_list.append(number)
if len(divisor_list) < 2:
print(user_in, "is a prime number!")
return
else:
print(user_in, "is not a prime number!")
return
main()