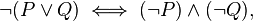LiquidHaskell: нарушение закона Деморгана

Question

У меня проблемы с доказательством следующего закона с LiquidHaskell:

Он известен как (один из) закон Деморгана, и просто утверждает, что отрицание orДва значения должны быть такими же, как andотрицание каждого. Это было доказано в течение долгого времени и является примером в руководстве LiquidHaskell. Я следую в учебнике, но не могу передать следующий код:

-- Test.hs
module Main where

main :: IO ()
main = return ()

(==>) :: Bool -> Bool -> Bool
False ==> False = True
False ==> True  = True
True  ==> True  = True
True  ==> False = False

(<=>)  :: Bool -> Bool -> Bool
False <=> False = True
False <=> True  = False
True  <=> True  = True
True  <=> False = False

{-@ type TRUE  = {v:Bool | Prop v}       @-}
{-@ type FALSE = {v:Bool | not (Prop v)} @-}

{-@ deMorgan :: Bool -> Bool -> TRUE @-}
deMorgan :: Bool -> Bool -> Bool
deMorgan a b = not (a || b) <=> (not a && not b)

При беге liquid Test.hsЯ получаю следующий вывод:

LiquidHaskell Copyright 2009-15 Regents of the University of California. All Rights Reserved.


**** DONE:  Parsed All Specifications ******************************************


**** DONE:  Loaded Targets *****************************************************


**** DONE:  Extracted Core using GHC *******************************************

Working   0%     [.................................................................]
Done solving.

**** DONE:  solve **************************************************************


**** DONE:  annotate ***********************************************************


**** RESULT: UNSAFE ************************************************************


 Test.hs:23:16-48: Error: Liquid Type Mismatch

 23 | deMorgan a b = not (a || b) <=> (not a && not b)
                     ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^

   Inferred type
     VV : Bool

   not a subtype of Required type
     VV : {VV : Bool | Prop VV}

   In Context

Теперь я ни в коем случае не эксперт LiquidHaskell, но я почти уверен, что что-то не так. Я убедил себя, что идентичность сохраняется несколько лет назад, но чтобы убедиться, что я вызывал функцию при каждом возможном вводе, и в конце концов запустил

λ: :l Test.hs 
λ: import Test.QuickCheck
λ: quickCheck deMorgan 
>>> +++ OK, passed 100 tests.

Таким образом, у меня, похоже, нет опечатки в коде на Haskell, ошибка должна лежать в спецификации LiquidHaskell. Кажется, что LiquidHaskell не может сделать вывод, что в результате Bool строго TRUE:

Inferred type
  VV : Bool

not a subtype of Required type
  VV : {VV : Bool | Prop VV}

В чем моя ошибка здесь? Любая помощь приветствуется!

PS: я использую z3 решатель, и работает GHC 7.10.3. Версия LiquidHaskell 2009-15,

Answer 1

LiquidHaskell не может доказать вашу программу безопасной, потому что она не имеет достаточно сильный тип для (<=>), Мы делаем типы для функций, но вывод основан на сигнатурах других типов в программе. В частности, мы должны выяснить, что

{-@ (<=>) :: p:Bool -> q:Bool -> {v:Bool | Prop v <=> (Prop p <=> Prop q)} @-}

(The Prop Синтаксис, как мы поднимаем Haskell Bool к логическому SMT.)

Чтобы LiquidHaskell мог вывести этот тип, ему нужно увидеть предикат Prop v <=> (Prop p <=> Prop q) где-то в подписи другого типа (для некоторых v, p, а также q). Этот фрагмент нигде не появляется, поэтому нам нужно явно указать подпись.

Это прискорбное ограничение LiquidHaskell, но оно крайне важно для сохранения решимости.

PS: Вот ссылка на рабочую версию вашего примера. http://goto.ucsd.edu:8090/index.html