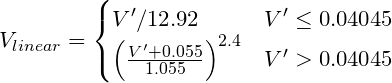Формула для определения яркости цвета RGB
Я ищу какую-то формулу или алгоритм для определения яркости цвета с учетом значений RGB. Я знаю, что это не может быть так просто, как сложить значения RGB вместе и получить более высокие суммы, чтобы быть ярче, но я не знаю, с чего начать.
24 ответа
Вы имеете в виду яркость? Воспринимаемая яркость? Светимость?
- Яркость (стандарт для определенных цветовых пространств):
(0.2126*R + 0.7152*G + 0.0722*B)[1] - Яркость (воспринимается вариант 1):
(0.299*R + 0.587*G + 0.114*B)[2] - Яркость (воспринимается вариант 2, медленнее для расчета):
sqrt( 0.241*R^2 + 0.691*G^2 + 0.068*B^2 )→sqrt( 0.299*R^2 + 0.587*G^2 + 0.114*B^2 )(спасибо Matthew Herbst) [3]
Я думаю, что вы ищете формулу преобразования RGB -> Luma.
Фотометрический / цифровой ITU BT.709:
Y = 0.2126 R + 0.7152 G + 0.0722 B
Цифровой ITU BT.601 (придает больший вес компонентам R и B):
Y = 0.299 R + 0.587 G + 0.114 B
Если вы хотите обменять точность на производительность, для этого есть две формулы аппроксимации:
Y = 0.33 R + 0.5 G + 0.16 B
Y = 0.375 R + 0.5 G + 0.125 B
Их можно быстро рассчитать как
Y = (R+R+B+G+G+G)/6
Y = (R+R+R+B+G+G+G+G)>>3
"Принятый" ответ неправильный и неполный
Единственные точные ответы - это ответы @jive-dadson и @EddingtonsMonkey, а также в support @nils-pipenbrinck. Другие ответы (включая принятые) содержат ссылки или цитируют источники, которые являются либо неправильными, неактуальными, устаревшими или поврежденными.
Вкратце:
- sRGB необходимо ЛИНЕЙНИЗИРОВАТЬ перед применением коэффициентов.
- Яркость (L или Y) линейна, как и свет.
- Воспринимаемая легкость (L*) нелинейна, как и человеческое восприятие.
- HSV и HSL даже отдаленно не точны с точки зрения восприятия.
- Стандарт IEC для sRGB определяет порог 0,04045, это НЕ 0,03928 (это было из устаревшей ранней версии).
- Чтобы быть полезными (т.е. относительно восприятия), евклидовы расстояния требуют перцептуально однородного декартова векторного пространства, такого как CIELAB. sRGB не тот.
Ниже приводится правильный и полный ответ:
Поскольку эта ветка широко используется в поисковых системах, я добавляю этот ответ, чтобы прояснить различные заблуждения по этому вопросу.
Яркость - это атрибут восприятия, у нее нет прямого измерения.
Воспринимаемая легкость измеряется некоторыми моделями зрения, такими как CIELAB, здесь L* (Lstar) является мерой воспринимаемой легкости и является нелинейной, чтобы аппроксимировать кривую нелинейного отклика человеческого зрения.
Яркость - это линейная мера света, спектрально взвешенная для нормального зрения, но не скорректированная для нелинейного восприятия легкости.
Яркость (Y´ prime) - это гамма-кодированный, взвешенный сигнал, используемый в некоторых кодировках видео. Не следует путать с линейной яркостью.
Гамма или кривая передачи (TRC) - это кривая, которая часто похожа на кривую восприятия, и обычно применяется к данным изображения для хранения или трансляции, чтобы уменьшить воспринимаемый шум и / или улучшить использование данных (и связанные с этим причины).
Чтобы определить воспринимаемую легкость, сначала преобразуйте гамма-кодированные значения изображения R´G´B´ в линейную яркость (L или Y), а затем к нелинейной воспринимаемой легкости (L*)
НАЙТИ ОСВЕЩЕННОСТЬ:
... Потому что видимо где-то потерялся...
Первый шаг:
Преобразование всех 8-битных целочисленных значений sRGB в десятичные 0,0–1,0
vR = sR / 255;
vG = sG / 255;
vB = sB / 255;
Шаг второй:
Преобразование гамма-кодированного RGB в линейное значение. sRGB (компьютерный стандарт), например, требует кривой мощности приблизительно V^2,2, хотя "точное" преобразование:
Где V´ - это гамма-кодированный канал R, G или B sRGB.
Псевдокод:
function sRGBtoLin(colorChannel) {
// Send this function a decimal sRGB gamma encoded color value
// between 0.0 and 1.0, and it returns a linearized value.
if ( colorChannel <= 0.04045 ) {
return colorChannel / 12.92;
} else {
return pow((( colorChannel + 0.055)/1.055),2.4));
}
}
Шаг третий:
Чтобы найти яркость (Y), примените стандартные коэффициенты для sRGB:
Псевдокод с использованием вышеуказанных функций:
Y = (0.2126 * sRGBtoLin(vR) + 0.7152 * sRGBtoLin(vG) + 0.0722 * sRGBtoLin(vB))
ЧТОБЫ НАЙТИ ПРЕДСТАВЛЕННУЮ ЛЕГКОСТЬ:
Шаг четвертый:
Возьмите яркость Y сверху и преобразуйте в L*
function YtoLstar(Y) {
// Send this function a luminance value between 0.0 and 1.0,
// and it returns L* which is "perceptual lightness"
if ( Y <= (216/24389) { // The CIE standard states 0.008856 but 216/24389 is the intent for 0.008856451679036
return Y * (24389/27); // The CIE standard states 903.3, but 24389/27 is the intent, making 903.296296296296296
} else {
return pow(Y,(1/3)) * 116 - 16;
}
}
L * - это значение от 0 (черный) до 100 (белый), где 50 - это воспринимаемый "средний серый". L* = 50 эквивалентно Y = 18,4 или, другими словами, 18% -ная серая карта, представляющая середину фотографической экспозиции (зона Анселя Адамса V).
Ссылки:
IEC 61966-2-1:1999 Standard
Wikipedia sRGB
Wikipedia CIELAB
Wikipedia CIEXYZ
Гамма Чарльза Пойнтона FAQ
Я сделал сравнение трех алгоритмов в принятом ответе. Я генерировал цвета в цикле, где использовался только каждый 400-й цвет. Каждый цвет представлен 2x2 пикселя, цвета сортируются от самых темных к самым светлым (слева направо, сверху вниз).
1-й рисунок - яркость (относительная)
0.2126 * R + 0.7152 * G + 0.0722 * B
2-я картинка - http://www.w3.org/TR/AERT
0.299 * R + 0.587 * G + 0.114 * B
3-я картина - HSP Color Model
sqrt(0.299 * R^2 + 0.587 * G^2 + 0.114 * B^2)
4-е изображение - формула относительной яркости и контрастности WCAG 2.0 SC 1.4.3 (см Synchro Ответ Synchro)
На 1-м и 2-м снимках иногда можно увидеть рисунок в зависимости от количества цветов в одном ряду. Я никогда не замечал никаких паттернов на картинке из 3-го или 4-го алгоритма.
Если бы мне пришлось выбирать, я бы пошел с алгоритмом № 3, так как его гораздо проще реализовать и он примерно на 33% быстрее, чем 4-й.

Ниже приведен единственный ПРАВИЛЬНЫЙ алгоритм для преобразования изображений sRGB, используемых в браузерах и т. Д., В оттенки серого.
Необходимо применить инверсию гамма-функции для цветового пространства перед вычислением внутреннего произведения. Затем вы применяете гамма-функцию к уменьшенному значению. Невыполнение гамма-функции может привести к ошибкам до 20%.
Для типичных компьютерных вещей цветовое пространство sRGB. Правильные цифры для sRGB - ок. 0,21, 0,72, 0,07. Гамма для sRGB - это составная функция, которая приближает возведение в степень на 1/(2.2). Здесь все это в C++.
// sRGB luminance(Y) values
const double rY = 0.212655;
const double gY = 0.715158;
const double bY = 0.072187;
// Inverse of sRGB "gamma" function. (approx 2.2)
double inv_gam_sRGB(int ic) {
double c = ic/255.0;
if ( c <= 0.04045 )
return c/12.92;
else
return pow(((c+0.055)/(1.055)),2.4);
}
// sRGB "gamma" function (approx 2.2)
int gam_sRGB(double v) {
if(v<=0.0031308)
v *= 12.92;
else
v = 1.055*pow(v,1.0/2.4)-0.055;
return int(v*255+0.5); // This is correct in C++. Other languages may not
// require +0.5
}
// GRAY VALUE ("brightness")
int gray(int r, int g, int b) {
return gam_sRGB(
rY*inv_gam_sRGB(r) +
gY*inv_gam_sRGB(g) +
bY*inv_gam_sRGB(b)
);
}
Вместо того, чтобы заблудиться среди случайного выбора формул, упомянутых здесь, я предлагаю вам перейти на формулу, рекомендованную стандартами W3C.
Вот простая, но точная реализация PHP формул относительной яркости и контрастности WCAG 2.0 SC 1.4.3. Он выдает значения, которые подходят для оценки соотношений, необходимых для соответствия WCAG, как на этой странице, и как таковые подходят и подходят для любого веб-приложения. Это тривиально портировать на другие языки.
/**
* Calculate relative luminance in sRGB colour space for use in WCAG 2.0 compliance
* @link http://www.w3.org/TR/WCAG20/#relativeluminancedef
* @param string $col A 3 or 6-digit hex colour string
* @return float
* @author Marcus Bointon <marcus@synchromedia.co.uk>
*/
function relativeluminance($col) {
//Remove any leading #
$col = trim($col, '#');
//Convert 3-digit to 6-digit
if (strlen($col) == 3) {
$col = $col[0] . $col[0] . $col[1] . $col[1] . $col[2] . $col[2];
}
//Convert hex to 0-1 scale
$components = array(
'r' => hexdec(substr($col, 0, 2)) / 255,
'g' => hexdec(substr($col, 2, 2)) / 255,
'b' => hexdec(substr($col, 4, 2)) / 255
);
//Correct for sRGB
foreach($components as $c => $v) {
if ($v <= 0.03928) {
$components[$c] = $v / 12.92;
} else {
$components[$c] = pow((($v + 0.055) / 1.055), 2.4);
}
}
//Calculate relative luminance using ITU-R BT. 709 coefficients
return ($components['r'] * 0.2126) + ($components['g'] * 0.7152) + ($components['b'] * 0.0722);
}
/**
* Calculate contrast ratio acording to WCAG 2.0 formula
* Will return a value between 1 (no contrast) and 21 (max contrast)
* @link http://www.w3.org/TR/WCAG20/#contrast-ratiodef
* @param string $c1 A 3 or 6-digit hex colour string
* @param string $c2 A 3 or 6-digit hex colour string
* @return float
* @author Marcus Bointon <marcus@synchromedia.co.uk>
*/
function contrastratio($c1, $c2) {
$y1 = relativeluminance($c1);
$y2 = relativeluminance($c2);
//Arrange so $y1 is lightest
if ($y1 < $y2) {
$y3 = $y1;
$y1 = $y2;
$y2 = $y3;
}
return ($y1 + 0.05) / ($y2 + 0.05);
}
Чтобы добавить то, что сказали все остальные:
Все эти уравнения работают довольно хорошо на практике, но если вам нужно быть очень точным, вам нужно сначала преобразовать цвет в линейное цветовое пространство (применить обратную гамму изображения), сделать средневзвешенное значение основных цветов и - если вы хотите, чтобы отобразить цвет - вернуть яркость обратно в гамму монитора.
Разница в яркости между поглощением гаммы и выполнением правильной гаммы составляет до 20% в темных серых тонах.
Я нашел этот код (написанный на C#), который отлично справляется с расчетом "яркости" цвета. В этом сценарии код пытается определить, нужно ли поместить белый или черный текст поверх цвета.
Интересно, что эта формулировка для RGB=>HSV просто использует v=MAX3(r,g,b). Другими словами, вы можете использовать максимум (r, g, b) как V в HSV.
Я проверил, и на странице 575 в Hearn & Baker они так же вычисляют "ценность".
Считайте это дополнением к отличному ответу Myndex . Как он (и другие) объясняет, алгоритмы вычисления относительной яркости (и воспринимаемой яркости) цвета RGB предназначены для работы с линейными значениями RGB. Вы не можете просто применить их к необработанным значениям sRGB и надеяться получить такие же результаты.
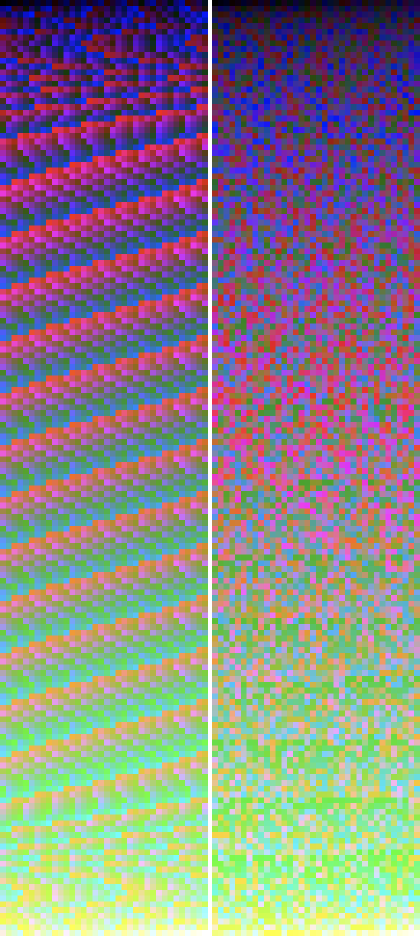
Что ж, в теории все это звучит великолепно, но мне действительно нужно было лично убедиться в этом, поэтому, вдохновленный цветовыми градиентами Петра Хуртака , я пошел дальше и сделал свой собственный. Они иллюстрируют два наиболее распространенных алгоритма (рекомендации ITU-R BT.601 и BT.709) и ясно демонстрируют, почему вы должны выполнять свои расчеты с линейными значениями (а не с гамма-коррекцией).
Во-первых, вот результаты более старого алгоритма ITU BT.601. Тот, что слева, использует необработанные значения sRGB. Тот, что справа, использует линейные значения.
Градиенты яркости цвета ITU-R BT.601
0,299 Р + 0,587 Г + 0,114 Б
При таком разрешении левый на самом деле выглядит на удивление хорошо! Но если присмотреться, можно увидеть несколько проблем. При более высоком разрешении нежелательные артефакты более очевидны:
Линейный этим не страдает, но шумов там довольно много. Давайте сравним его с рекомендацией ITU-R BT.709…
Градиенты яркости цвета ITU-R BT.709
0,2126 Р + 0,7152 Г + 0,0722 Б
О, парень. Явно не предназначен для использования с необработанными значениями sRGB! И тем не менее, это именно то, что делает большинство людей!
В высоком разрешении вы действительно можете увидеть, насколько эффективен этот алгоритм при использовании линейных значений. У него не так много шума, как у предыдущего. Хотя ни один из этих алгоритмов не идеален, этот почти настолько хорош, насколько это возможно.
Решал сегодня аналогичную задачу на javascript. Я остановился на этомgetPerceivedLightness(rgb)функция для цвета HEX RGB. Он имеет дело с эффектом Гельмгольца-Кольрауша с помощью формулы Фэйрчайлда и Перротта для коррекции яркости.
/**
* Converts RGB color to CIE 1931 XYZ color space.
* https://www.image-engineering.de/library/technotes/958-how-to-convert-between-srgb-and-ciexyz
* @param {string} hex
* @return {number[]}
*/
export function rgbToXyz(hex) {
const [r, g, b] = hexToRgb(hex).map(_ => _ / 255).map(sRGBtoLinearRGB)
const X = 0.4124 * r + 0.3576 * g + 0.1805 * b
const Y = 0.2126 * r + 0.7152 * g + 0.0722 * b
const Z = 0.0193 * r + 0.1192 * g + 0.9505 * b
// For some reason, X, Y and Z are multiplied by 100.
return [X, Y, Z].map(_ => _ * 100)
}
/**
* Undoes gamma-correction from an RGB-encoded color.
* https://en.wikipedia.org/wiki/SRGB#Specification_of_the_transformation
* https://stackru.com/questions/596216/formula-to-determine-brightness-of-rgb-color
* @param {number}
* @return {number}
*/
function sRGBtoLinearRGB(color) {
// Send this function a decimal sRGB gamma encoded color value
// between 0.0 and 1.0, and it returns a linearized value.
if (color <= 0.04045) {
return color / 12.92
} else {
return Math.pow((color + 0.055) / 1.055, 2.4)
}
}
/**
* Converts hex color to RGB.
* https://stackru.com/questions/5623838/rgb-to-hex-and-hex-to-rgb
* @param {string} hex
* @return {number[]} [rgb]
*/
function hexToRgb(hex) {
const match = /^#?([a-f\d]{2})([a-f\d]{2})([a-f\d]{2})$/i.exec(hex)
if (match) {
match.shift()
return match.map(_ => parseInt(_, 16))
}
}
/**
* Converts CIE 1931 XYZ colors to CIE L*a*b*.
* The conversion formula comes from <http://www.easyrgb.com/en/math.php>.
* https://github.com/cangoektas/xyz-to-lab/blob/master/src/index.js
* @param {number[]} color The CIE 1931 XYZ color to convert which refers to
* the D65/2° standard illuminant.
* @returns {number[]} The color in the CIE L*a*b* color space.
*/
// X, Y, Z of a "D65" light source.
// "D65" is a standard 6500K Daylight light source.
// https://en.wikipedia.org/wiki/Illuminant_D65
const D65 = [95.047, 100, 108.883]
export function xyzToLab([x, y, z]) {
[x, y, z] = [x, y, z].map((v, i) => {
v = v / D65[i]
return v > 0.008856 ? Math.pow(v, 1 / 3) : v * 7.787 + 16 / 116
})
const l = 116 * y - 16
const a = 500 * (x - y)
const b = 200 * (y - z)
return [l, a, b]
}
/**
* Converts Lab color space to Luminance-Chroma-Hue color space.
* http://www.brucelindbloom.com/index.html?Eqn_Lab_to_LCH.html
* @param {number[]}
* @return {number[]}
*/
export function labToLch([l, a, b]) {
const c = Math.sqrt(a * a + b * b)
const h = abToHue(a, b)
return [l, c, h]
}
/**
* Converts a and b of Lab color space to Hue of LCH color space.
* https://stackru.com/questions/53733379/conversion-of-cielab-to-cielchab-not-yielding-correct-result
* @param {number} a
* @param {number} b
* @return {number}
*/
function abToHue(a, b) {
if (a >= 0 && b === 0) {
return 0
}
if (a < 0 && b === 0) {
return 180
}
if (a === 0 && b > 0) {
return 90
}
if (a === 0 && b < 0) {
return 270
}
let xBias
if (a > 0 && b > 0) {
xBias = 0
} else if (a < 0) {
xBias = 180
} else if (a > 0 && b < 0) {
xBias = 360
}
return radiansToDegrees(Math.atan(b / a)) + xBias
}
function radiansToDegrees(radians) {
return radians * (180 / Math.PI)
}
function degreesToRadians(degrees) {
return degrees * Math.PI / 180
}
/**
* Saturated colors appear brighter to human eye.
* That's called Helmholtz-Kohlrausch effect.
* Fairchild and Pirrotta came up with a formula to
* calculate a correction for that effect.
* "Color Quality of Semiconductor and Conventional Light Sources":
* https://books.google.ru/books?id=ptDJDQAAQBAJ&pg=PA45&lpg=PA45&dq=fairchild+pirrotta+correction&source=bl&ots=7gXR2MGJs7&sig=ACfU3U3uIHo0ZUdZB_Cz9F9NldKzBix0oQ&hl=ru&sa=X&ved=2ahUKEwi47LGivOvmAhUHEpoKHU_ICkIQ6AEwAXoECAkQAQ#v=onepage&q=fairchild%20pirrotta%20correction&f=false
* @return {number}
*/
function getLightnessUsingFairchildPirrottaCorrection([l, c, h]) {
const l_ = 2.5 - 0.025 * l
const g = 0.116 * Math.abs(Math.sin(degreesToRadians((h - 90) / 2))) + 0.085
return l + l_ * g * c
}
export function getPerceivedLightness(hex) {
return getLightnessUsingFairchildPirrottaCorrection(labToLch(xyzToLab(rgbToXyz(hex))))
}
Вот немного кода C, который должен правильно рассчитать воспринимаемую яркость.
// reverses the rgb gamma
#define inverseGamma(t) (((t) <= 0.0404482362771076) ? ((t)/12.92) : pow(((t) + 0.055)/1.055, 2.4))
//CIE L*a*b* f function (used to convert XYZ to L*a*b*) http://en.wikipedia.org/wiki/Lab_color_space
#define LABF(t) ((t >= 8.85645167903563082e-3) ? powf(t,0.333333333333333) : (841.0/108.0)*(t) + (4.0/29.0))
float
rgbToCIEL(PIXEL p)
{
float y;
float r=p.r/255.0;
float g=p.g/255.0;
float b=p.b/255.0;
r=inverseGamma(r);
g=inverseGamma(g);
b=inverseGamma(b);
//Observer = 2°, Illuminant = D65
y = 0.2125862307855955516*r + 0.7151703037034108499*g + 0.07220049864333622685*b;
// At this point we've done RGBtoXYZ now do XYZ to Lab
// y /= WHITEPOINT_Y; The white point for y in D65 is 1.0
y = LABF(y);
/* This is the "normal conversion which produces values scaled to 100
Lab.L = 116.0*y - 16.0;
*/
return(1.16*y - 0.16); // return values for 0.0 >=L <=1.0
}
Как упоминал @Nils Pipenbrinck:
Все эти уравнения хорошо работают на практике, но если вам нужно быть очень точным, вы должны [сделать некоторые дополнительные действия с гаммой]. Разница в яркости между игнорированием гаммы и правильной гаммой составляет до 20% в темных оттенках серого.
Вот полностью автономная функция JavaScript, которая делает «дополнительные» вещи, чтобы получить эту дополнительную точность. Он основан на ответе Jive Dadson C++ на тот же вопрос.
// Returns perceived brightness (0-1) of the given 0-255 RGB values
// Based on this C++ implementation: https://stackoverflow.com/a/13558570/11950764
function rgbBrightness(r, g, b) {
let v = 0;
v += 0.212655 * ((r/255) <= 0.04045 ? (r/255)/12.92 : Math.pow(((r/255)+0.055)/1.055, 2.4));
v += 0.715158 * ((g/255) <= 0.04045 ? (g/255)/12.92 : Math.pow(((g/255)+0.055)/1.055, 2.4));
v += 0.072187 * ((b/255) <= 0.04045 ? (b/255)/12.92 : Math.pow(((b/255)+0.055)/1.055, 2.4));
return v <= 0.0031308 ? v*12.92 : 1.055 * Math.pow(v,1.0/2.4) - 0.055;
}
Интересно, как эти коэффициенты RGB были определены. Я сам провел эксперимент и в итоге получил следующее:
Y = 0.267 R + 0.642 G + 0.091 B
Близко, но очевидно отличается от давно установленных коэффициентов МСЭ. Интересно, могут ли эти коэффициенты быть разными для каждого наблюдателя, потому что у всех нас может быть разное количество колбочек и палочек на сетчатке в наших глазах, и особенно соотношение между разными колбочками может отличаться.
Для справки:
МСЭ BT.709:
Y = 0.2126 R + 0.7152 G + 0.0722 B
МСЭ BT.601:
Y = 0.299 R + 0.587 G + 0.114 B
Я выполнил тест, быстро переместив маленькую серую полоску на ярко-красный, ярко-зеленый и ярко-синий фон, и отрегулировал серый, пока он не смешался настолько, насколько это было возможно. Я также повторил этот тест с другими оттенками. Я повторил тест на разных дисплеях, даже на одном с фиксированным гамма-фактором 3,0, но для меня все выглядит одинаково. Более того, коэффициенты МСЭ буквально не соответствуют моим глазам.
И да, у меня, видимо, нормальное цветовое зрение.
Значение яркости RGB = 0,3 R + 0,59 G + 0,11 B
http://www.scantips.com/lumin.html
Если вы ищете, насколько близок белый цвет, вы можете использовать Евклидово расстояние от (255, 255, 255)
Я думаю, что цветовое пространство RGB заметно неоднородно по отношению к евклидову расстоянию L2. Унифицированные пространства включают CIE LAB и LUV.
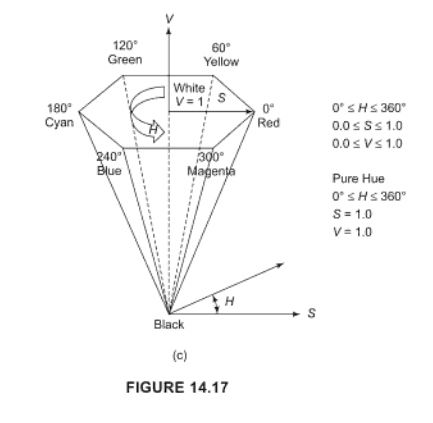
Цветовое пространство HSV должно помочь, см. Статью в Википедии в зависимости от языка, на котором вы работаете, вы можете получить преобразование библиотеки.
H это оттенок, который является числовым значением для цвета (то есть красный, зеленый...)
S - насыщенность цвета, т. Е. Насколько он интенсивный
V - это "яркость" цвета.
Формула обратной гаммы Джайва Дадсона должна быть удалена с половинной корректировкой при реализации в Javascript, то есть возвращение функции gam_sRGB должно возвращать int(v*255); не вернуть int(v*255+.5); Полу-корректировка округляется, и это может привести к значению, слишком высокому для R=G=B, то есть триады серого цвета. Преобразование в оттенках серого в триаде R=G=B должно давать значение, равное R; это одно из доказательств того, что формула верна. См. Nine Shades of Greyscale для формулы в действии (без половинной корректировки).
Ответ от Myindex, закодированный на Java:
public static double calculateRelativeLuminance(Color color)
{
double red = color.getRed() / 255.0;
double green = color.getGreen() / 255.0;
double blue = color.getBlue() / 255.0;
double r = (red <= 0.04045) ? red / 12.92 : Math.pow((red + 0.055) / 1.055, 2.4);
double g = (green <= 0.04045) ? green / 12.92 : Math.pow((green + 0.055) / 1.055, 2.4);
double b = (blue <= 0.04045) ? blue / 12.92 : Math.pow((blue + 0.055) / 1.055, 2.4);
return 0.2126 * r + 0.7152 * g + 0.0722 * b;
}
Я использовал его, чтобы вычислить коэффициент контрастности цвета фона и определить, будет ли цвет текста ярким или нет. Полный пример:
public static boolean isBright(Color backgroundColor)
{
double backgroundLuminance = calculateRelativeLuminance(backgroundColor);
double whiteContrastRatio = calculateContrastRatio(backgroundLuminance, 1.0);
double blackContrastRatio = calculateContrastRatio(backgroundLuminance, 0.0);
return whiteContrastRatio > blackContrastRatio;
}
public static double calculateRelativeLuminance(Color color)
{
double red = color.getRed() / 255.0;
double green = color.getGreen() / 255.0;
double blue = color.getBlue() / 255.0;
double r = (red <= 0.04045) ? red / 12.92 : Math.pow((red + 0.055) / 1.055, 2.4);
double g = (green <= 0.04045) ? green / 12.92 : Math.pow((green + 0.055) / 1.055, 2.4);
double b = (blue <= 0.04045) ? blue / 12.92 : Math.pow((blue + 0.055) / 1.055, 2.4);
return 0.2126 * r + 0.7152 * g + 0.0722 * b;
}
public static double calculateContrastRatio(double backgroundLuminance, double textLuminance)
{
var brightest = Math.max(backgroundLuminance, textLuminance);
var darkest = Math.min(backgroundLuminance, textLuminance);
return (brightest + 0.05) / (darkest + 0.05);
}
Эта ссылка подробно объясняет все, в том числе, почему эти константы множителя существуют до значений R, G и B.
Изменить: Здесь также есть объяснение одному из ответов (0,299*R + 0,587*G + 0,114*B)
Мой ПРОСТОЙ вывод , основанный на всех этих ответах, для большинства практических случаев вам нужно только:
brightness = 0.2*r + 0.7*g + 0.1*b
Когда значения r, g,b находятся в диапазоне от 0 до 255, шкала яркости также находится в диапазоне от 0 (= черный) до 255 (= белый).
Это можно настроить, но обычно в этом нет необходимости.
Для ясности, формулы, которые используют квадратный корень должны быть
sqrt(coefficient * (colour_value^2))
не
sqrt((coefficient * colour_value))^2
Доказательством этого является преобразование триады R=G=B в оттенки серого R. Это будет верно только в том случае, если вы возводите в квадрат значение цвета, а не коэффициент времени, равный временному значению цвета. См Девять оттенков серого
"V" HSV, вероятно, то, что вы ищете. MATLAB имеет функцию rgb2hsv, а ранее цитированная статья в Википедии полна псевдокода. Если преобразование RGB2HSV невозможно, менее точной моделью будет версия изображения в градациях серого.
Чтобы определить яркость цвета с помощью R, я конвертирую цвет системы RGB в цвет системы HSV.
В моем сценарии я использую системный код HEX раньше по другой причине, но вы также можете начать с системного кода RGB с помощью rgb2hsv {grDevices}, Документация здесь.
Вот эта часть моего кода:
sample <- c("#010101", "#303030", "#A6A4A4", "#020202", "#010100")
hsvc <-rgb2hsv(col2rgb(sample)) # convert HEX to HSV
value <- as.data.frame(hsvc) # create data.frame
value <- value[3,] # extract the information of brightness
order(value) # ordrer the color by brightness
Пожалуйста, определите яркость. Если вы ищете, насколько близок белый цвет, вы можете использовать Евклидово расстояние от (255, 255, 255)