Рассчитать площадь пересечения двух повернутых прямоугольников в питоне
У меня есть два 2D повернутых прямоугольника, определенных как (центр x, центр y, высота, ширина) и угол поворота (0-360°). Как бы я вычислил площадь пересечения этих двух повернутых прямоугольников.
3 ответа
Такие задачи решаются с использованием пакетов вычислительной геометрии, например Shapely:
import shapely.geometry
import shapely.affinity
class RotatedRect:
def __init__(self, cx, cy, w, h, angle):
self.cx = cx
self.cy = cy
self.w = w
self.h = h
self.angle = angle
def get_contour(self):
w = self.w
h = self.h
c = shapely.geometry.box(-w/2.0, -h/2.0, w/2.0, h/2.0)
rc = shapely.affinity.rotate(c, self.angle)
return shapely.affinity.translate(rc, self.cx, self.cy)
def intersection(self, other):
return self.get_contour().intersection(other.get_contour())
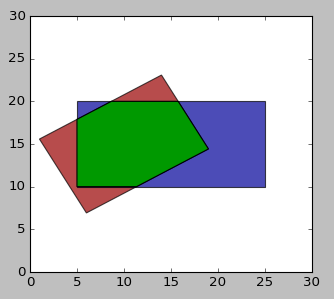
r1 = RotatedRect(10, 15, 15, 10, 30)
r2 = RotatedRect(15, 15, 20, 10, 0)
from matplotlib import pyplot
from descartes import PolygonPatch
fig = pyplot.figure(1, figsize=(10, 4))
ax = fig.add_subplot(121)
ax.set_xlim(0, 30)
ax.set_ylim(0, 30)
ax.add_patch(PolygonPatch(r1.get_contour(), fc='#990000', alpha=0.7))
ax.add_patch(PolygonPatch(r2.get_contour(), fc='#000099', alpha=0.7))
ax.add_patch(PolygonPatch(r1.intersection(r2), fc='#009900', alpha=1))
pyplot.show()
Вот решение, которое не использует никаких библиотек за пределами стандартной библиотеки Python.
Определение площади пересечения двух прямоугольников можно разделить на две подзадачи:
- Нахождение многоугольника пересечения, если есть;
- Определить площадь пересечения полигона.
Обе проблемы относительно просты, когда вы работаете с вершинами (углами) прямоугольников. Итак, сначала вы должны определить эти вершины. Предполагая, что начало координат находится в центре прямоугольника, вершины начинаются с левого нижнего угла в направлении против часовой стрелки:(-w/2, -h/2), (w/2, -h/2), (w/2, h/2), а также (-w/2, h/2), Поворачивая это на угол aи переводя их в правильное положение центра прямоугольника, они становятся:(cx + (-w/2)cos(a) - (-h/2)sin(a), cy + (-w/2)sin(a) + (-h/2)cos(a))и аналогично для других угловых точек.
Простой способ определения полигона пересечения заключается в следующем: вы начинаете с одного прямоугольника в качестве возможного полигона пересечения. Затем вы применяете процесс последовательной резки (как описано здесь. Вкратце: вы берете все ребра второго прямоугольника по очереди и удаляете все части из предполагаемого многоугольника пересечения, которые находятся на "внешней" полуплоскости, определяемой ребром (в обоих направлениях). Делая это для всех ребер, вы оставляете полигон пересечения-кандидата только с теми частями, которые находятся внутри второго прямоугольника или на его границе.
Площадь результирующего многоугольника (определяемая серией вершин) может быть рассчитана по координатам вершин. Вы суммируете перекрестные произведения вершин каждого ребра (снова в порядке против часовой стрелки) и делите это на два. Смотрите, например, http://www.mathopenref.com/coordpolygonarea.html
Достаточно теории и объяснения. Вот код:
from math import pi, cos, sin
class Vector:
def __init__(self, x, y):
self.x = x
self.y = y
def __add__(self, v):
if not isinstance(v, Vector):
return NotImplemented
return Vector(self.x + v.x, self.y + v.y)
def __sub__(self, v):
if not isinstance(v, Vector):
return NotImplemented
return Vector(self.x - v.x, self.y - v.y)
def cross(self, v):
if not isinstance(v, Vector):
return NotImplemented
return self.x*v.y - self.y*v.x
class Line:
# ax + by + c = 0
def __init__(self, v1, v2):
self.a = v2.y - v1.y
self.b = v1.x - v2.x
self.c = v2.cross(v1)
def __call__(self, p):
return self.a*p.x + self.b*p.y + self.c
def intersection(self, other):
# See e.g. https://en.wikipedia.org/wiki/Line%E2%80%93line_intersection#Using_homogeneous_coordinates
if not isinstance(other, Line):
return NotImplemented
w = self.a*other.b - self.b*other.a
return Vector(
(self.b*other.c - self.c*other.b)/w,
(self.c*other.a - self.a*other.c)/w
)
def rectangle_vertices(cx, cy, w, h, r):
angle = pi*r/180
dx = w/2
dy = h/2
dxcos = dx*cos(angle)
dxsin = dx*sin(angle)
dycos = dy*cos(angle)
dysin = dy*sin(angle)
return (
Vector(cx, cy) + Vector(-dxcos - -dysin, -dxsin + -dycos),
Vector(cx, cy) + Vector( dxcos - -dysin, dxsin + -dycos),
Vector(cx, cy) + Vector( dxcos - dysin, dxsin + dycos),
Vector(cx, cy) + Vector(-dxcos - dysin, -dxsin + dycos)
)
def intersection_area(r1, r2):
# r1 and r2 are in (center, width, height, rotation) representation
# First convert these into a sequence of vertices
rect1 = rectangle_vertices(*r1)
rect2 = rectangle_vertices(*r2)
# Use the vertices of the first rectangle as
# starting vertices of the intersection polygon.
intersection = rect1
# Loop over the edges of the second rectangle
for p, q in zip(rect2, rect2[1:] + rect2[:1]):
if len(intersection) <= 2:
break # No intersection
line = Line(p, q)
# Any point p with line(p) <= 0 is on the "inside" (or on the boundary),
# any point p with line(p) > 0 is on the "outside".
# Loop over the edges of the intersection polygon,
# and determine which part is inside and which is outside.
new_intersection = []
line_values = [line(t) for t in intersection]
for s, t, s_value, t_value in zip(
intersection, intersection[1:] + intersection[:1],
line_values, line_values[1:] + line_values[:1]):
if s_value <= 0:
new_intersection.append(s)
if s_value * t_value < 0:
# Points are on opposite sides.
# Add the intersection of the lines to new_intersection.
intersection_point = line.intersection(Line(s, t))
new_intersection.append(intersection_point)
intersection = new_intersection
# Calculate area
if len(intersection) <= 2:
return 0
return 0.5 * sum(p.x*q.y - p.y*q.x for p, q in
zip(intersection, intersection[1:] + intersection[:1]))
if __name__ == '__main__':
r1 = (10, 15, 15, 10, 30)
r2 = (15, 15, 20, 10, 0)
print(intersection_area(r1, r2))
intersection, pnt = contourIntersection(rect1, rect2)
После просмотра возможной страницы-дубликата для этой проблемы я не смог найти законченный ответ для python, поэтому вот мое решение с использованием маскировки. Эта функция будет работать со сложными фигурами под любым углом, а не только с прямоугольниками
Вы передаете 2 контура повернутых прямоугольников в качестве параметров, и он возвращает "Нет", если пересечение не происходит или изображение пересеченной области и положение левой / верхней части этого изображения относительно исходного изображения, из которого были взяты контуры
Использует python, cv2 и numpy
import cv2
import math
import numpy as np
def contourIntersection(con1, con2, showContours=False):
# skip if no bounding rect intersection
leftmost1 = tuple(con1[con1[:, :, 0].argmin()][0])
topmost1 = tuple(con1[con1[:, :, 1].argmin()][0])
leftmost2 = tuple(con2[con2[:, :, 0].argmin()][0])
topmost2 = tuple(con2[con2[:, :, 1].argmin()][0])
rightmost1 = tuple(con1[con1[:, :, 0].argmax()][0])
bottommost1 = tuple(con1[con1[:, :, 1].argmax()][0])
rightmost2 = tuple(con2[con2[:, :, 0].argmax()][0])
bottommost2 = tuple(con2[con2[:, :, 1].argmax()][0])
if rightmost1[0] < leftmost2[0] or rightmost2[0] < leftmost1[0] or bottommost1[1] < topmost2[1] or bottommost2[1] < topmost1[1]:
return None, None
# reset top / left to 0
left = leftmost1[0] if leftmost1[0] < leftmost2[0] else leftmost2[0]
top = topmost1[1] if topmost1[1] < topmost2[1] else topmost2[1]
newCon1 = []
for pnt in con1:
newLeft = pnt[0][0] - left
newTop = pnt[0][1] - top
newCon1.append([newLeft, newTop])
# next
con1_new = np.array([newCon1], dtype=np.int32)
newCon2 = []
for pnt in con2:
newLeft = pnt[0][0] - left
newTop = pnt[0][1] - top
newCon2.append([newLeft, newTop])
# next
con2_new = np.array([newCon2], dtype=np.int32)
# width / height
right1 = rightmost1[0] - left
bottom1 = bottommost1[1] - top
right2 = rightmost2[0] - left
bottom2 = bottommost2[1] - top
width = right1 if right1 > right2 else right2
height = bottom1 if bottom1 > bottom2 else bottom2
# create images
img1 = np.zeros([height, width], np.uint8)
cv2.drawContours(img1, con1_new, -1, (255, 255, 255), -1)
img2 = np.zeros([height, width], np.uint8)
cv2.drawContours(img2, con2_new, -1, (255, 255, 255), -1)
# mask images together using AND
imgIntersection = cv2.bitwise_and(img1, img2)
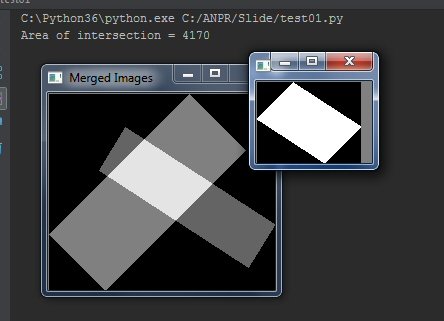
if showContours:
img1[img1 > 254] = 128
img2[img2 > 254] = 100
imgAll = cv2.bitwise_or(img1, img2)
cv2.imshow('Merged Images', imgAll)
# end if
if not imgIntersection.sum():
return None, None
# trim
while not imgIntersection[0].sum():
imgIntersection = np.delete(imgIntersection, (0), axis=0)
top += 1
while not imgIntersection[-1].sum():
imgIntersection = np.delete(imgIntersection, (-1), axis=0)
while not imgIntersection[:, 0].sum():
imgIntersection = np.delete(imgIntersection, (0), axis=1)
left += 1
while not imgIntersection[:, -1].sum():
imgIntersection = np.delete(imgIntersection, (-1), axis=1)
return imgIntersection, (left, top)
# end function
Чтобы завершить ответ, чтобы вы могли использовать вышеуказанную функцию со значениями CenterX, CenterY, Width, Height и Angle 2 повернутых прямоугольников, я добавил нижеприведенные функции. Просто измените свойства Rect1 и Rect2 в нижней части кода на свои собственные
def pixelsBetweenPoints(xy1, xy2):
X = abs(xy1[0] - xy2[0])
Y = abs(xy1[1] - xy2[1])
return int(math.sqrt((X ** 2) + (Y ** 2)))
# end function
def rotatePoint(angle, centerPoint, dist):
xRatio = math.cos(math.radians(angle))
yRatio = math.sin(math.radians(angle))
xPotted = int(centerPoint[0] + (dist * xRatio))
yPlotted = int(centerPoint[1] + (dist * yRatio))
newPoint = [xPotted, yPlotted]
return newPoint
# end function
def angleBetweenPoints(pnt1, pnt2):
A_B = pixelsBetweenPoints(pnt1, pnt2)
pnt3 = (pnt1[0] + A_B, pnt1[1])
C = pixelsBetweenPoints(pnt2, pnt3)
angle = math.degrees(math.acos((A_B * A_B + A_B * A_B - C * C) / (2.0 * A_B * A_B)))
# reverse if above horizon
if pnt2[1] < pnt1[1]:
angle = angle * -1
# end if
return angle
# end function
def rotateRectContour(xCenter, yCenter, height, width, angle):
# calc positions
top = int(yCenter - (height / 2))
left = int(xCenter - (width / 2))
right = left + width
rightTop = (right, top)
centerPoint = (xCenter, yCenter)
# new right / top point
rectAngle = angleBetweenPoints(centerPoint, rightTop)
angleRightTop = angle + rectAngle
angleRightBottom = angle + 180 - rectAngle
angleLeftBottom = angle + 180 + rectAngle
angleLeftTop = angle - rectAngle
distance = pixelsBetweenPoints(centerPoint, rightTop)
rightTop_new = rotatePoint(angleRightTop, centerPoint, distance)
rightBottom_new = rotatePoint(angleRightBottom, centerPoint, distance)
leftBottom_new = rotatePoint(angleLeftBottom, centerPoint, distance)
leftTop_new = rotatePoint(angleLeftTop, centerPoint, distance)
contourList = [[leftTop_new], [rightTop_new], [rightBottom_new], [leftBottom_new]]
contour = np.array(contourList, dtype=np.int32)
return contour
# end function
# rect1
xCenter_1 = 40
yCenter_1 = 20
height_1 = 200
width_1 = 80
angle_1 = 45
rect1 = rotateRectContour(xCenter_1, yCenter_1, height_1, width_1, angle_1)
# rect2
xCenter_2 = 80
yCenter_2 = 25
height_2 = 180
width_2 = 50
angle_2 = 123
rect2 = rotateRectContour(xCenter_2, yCenter_2, height_2, width_2, angle_2)
intersection, pnt = contourIntersection(rect1, rect2, True)
if intersection is None:
print('No intersection')
else:
print('Area of intersection = ' + str(int(intersection.sum() / 255)))
cv2.imshow('Intersection', intersection)
# end if
cv2.waitKey(0)