Лучший способ "зацикливания на 2-D массиве", используя Repa
Я нахожу библиотеку массивов Repa для Haskell очень интересной и хотела сделать простую программу, чтобы попытаться понять, как ее использовать. Я также сделал простую реализацию, используя списки, которые оказались намного быстрее. Мой главный вопрос - как я мог бы улучшить приведенный ниже код Repa, чтобы сделать его максимально эффективным (и, надеюсь, также очень читабельным). Я довольно новичок в использовании Haskell, и я не смог найти ни одного легко понятного учебника по Repa [ править, есть один на Haskell Wiki, который я почему-то забыл, когда писал это], так что не думайте, что я ничего не знаю.:) Например, я не уверен, когда использовать force или deepSeqArray.
Программа используется для приблизительного расчета объема сферы следующим образом:
- Указывается центральная точка и радиус сферы, а также равноотстоящие координаты внутри кубоида, которые, как известно, охватывают сферу.
- Программа берет каждую из координат, вычисляет расстояние до центра сферы, и если оно меньше радиуса сферы, оно используется для суммирования общего (приблизительного) объема сферы.
Ниже показаны две версии, одна из которых использует списки, а другая - repa. Я знаю, что код неэффективен, особенно для этого варианта использования, но идея состоит в том, чтобы сделать его позже более сложным.
Для приведенных ниже значений и компиляции с помощью "ghc -Odph -fllvm -fforce-Recomp -rtsopts -threaded" версия списка занимает 1,4 с, а версия repa - 12 с с помощью +RTS -N1 и 10 с с помощью +RTS -N2, хотя искры не преобразуются (у меня двухъядерный компьютер Intel (Core 2 Duo E7400 @ 2,8 ГГц) под управлением Windows 7 64, GHC 7.0.2 и llvm 2.8). (Закомментируйте правильную строку в главном ниже, чтобы просто запустить одну из версий.)
Спасибо за любую помощь!
import Data.Array.Repa as R
import qualified Data.Vector.Unboxed as V
import Prelude as P
-- Calculate the volume of a sphere by putting it in a bath of coordinates. Generate coordinates (x,y,z) in a cuboid. Then, for each coordinate, check if it is inside the sphere. Sum those coordinates and multiply by the coordinate grid step size to find an approximate volume.
particles = [(0,0,0)] -- used for the list alternative --[(0,0,0),(0,2,0)]
particles_repa = [0,0,0::Double] -- used for the repa alternative, can currently just be one coordinate
-- Radius of the particle
a = 4
-- Generate the coordinates. Could this be done more efficiently, and at the same time simple? In Matlab I would use ndgrid.
step = 0.1 --0.05
xrange = [-10,-10+step..10] :: [Double]
yrange = [-10,-10+step..10]
zrange = [-10,-10+step..10]
-- All coordinates as triples. These are used directly in the list version below.
coords = [(x,y,z) | x <- xrange, y <- yrange, z <- zrange]
---- List code ----
volumeIndividuals = fromIntegral (length particles) * 4*pi*a**3/3
volumeInside = step**3 * fromIntegral (numberInsideParticles particles coords)
numberInsideParticles particles coords = length $ filter (==True) $ P.map (insideParticles particles) coords
insideParticles particles coord = any (==True) $ P.map (insideParticle coord) particles
insideParticle (xc,yc,zc) (xp,yp,zp) = ((xc-xp)^2+(yc-yp)^2+(zc-zp)^2) < a**2
---- End list code ----
---- Repa code ----
-- Put the coordinates in a Nx3 array.
xcoords = P.map (\(x,_,_) -> x) coords
ycoords = P.map (\(_,y,_) -> y) coords
zcoords = P.map (\(_,_,z) -> z) coords
-- Total number of coordinates
num_coords = (length xcoords) ::Int
xcoords_r = fromList (Z :. num_coords :. (1::Int)) xcoords
ycoords_r = fromList (Z :. num_coords :. (1::Int)) ycoords
zcoords_r = fromList (Z :. num_coords :. (1::Int)) zcoords
rcoords = xcoords_r R.++ ycoords_r R.++ zcoords_r
-- Put the particle coordinates in an array, then extend (replicate) this array so that its size becomes the same as that of rcoords
particle = fromList (Z :. (1::Int) :. (3::Int)) particles_repa
particle_slice = slice particle (Z :. (0::Int) :. All)
particle_extended = extend (Z :. num_coords :. All) particle_slice
-- Calculate the squared difference between the (x,y,z) coordinates of the particle and the coordinates of the cuboid.
squared_diff = deepSeqArrays [rcoords,particle_extended] ((force2 rcoords) -^ (force2 particle_extended)) **^ 2
(**^) arr pow = R.map (**pow) arr
xslice = slice squared_diff (Z :. All :. (0::Int))
yslice = slice squared_diff (Z :. All :. (1::Int))
zslice = slice squared_diff (Z :. All :. (2::Int))
-- Calculate the distance between each coordinate and the particle center
sum_squared_diff = [xslice,yslice,zslice] `deepSeqArrays` xslice +^ yslice +^ zslice
-- Do the rest using vector, since I didn't get the repa variant working.
ssd_vec = toVector sum_squared_diff
-- Determine the number of the coordinates that are within the particle (instead of taking the square root to get the distances above, I compare to the square of the radius here, to improve performance)
total_within = fromIntegral (V.length $ V.filter (<a**2) ssd_vec)
--total_within = foldAll (\x acc -> if x < a**2 then acc+1 else acc) 0 sum_squared_diff
-- Finally, calculate an approximation of the volume of the sphere by taking the volume of the cubes with side step, multiplied with the number of coordinates within the sphere.
volumeInside_repa = step**3 * total_within
-- Helper function that shows the size of a 2-D array.
rsize = reverse . listOfShape . (extent :: Array DIM2 Double -> DIM2)
---- End repa code ----
-- Comment out the list or the repa version if you want to time the calculations separately.
main = do
putStrLn $ "Step = " P.++ show step
putStrLn $ "Volume of individual particles = " P.++ show volumeIndividuals
putStrLn $ "Volume of cubes inside particles (list) = " P.++ show volumeInside
putStrLn $ "Volume of cubes inside particles (repa) = " P.++ show volumeInside_repa
Редактировать: некоторый фон, который объясняет, почему я написал код, как указано выше:
Я в основном пишу код на Matlab, и мой опыт повышения производительности происходит в основном из этой области. В Matlab вы обычно хотите выполнять свои вычисления, используя функции, работающие непосредственно с матрицами, для повышения производительности. Моя реализация описанной выше проблемы в Matlab R2010b занимает 0,9 секунды с использованием версии матрицы, показанной ниже, и 15 секунд с использованием вложенных циклов. Хотя я знаю, что Haskell сильно отличается от Matlab, я надеялся, что переход от использования списков к использованию массивов Repa в Haskell улучшит производительность кода. Преобразования из списков-> массивов репа-> векторов есть, потому что я не достаточно квалифицирован, чтобы заменить их чем-то лучшим. Вот почему я прошу для ввода.:) Таким образом, приведенные выше временные числа субъективны, поскольку они могут измерять мою производительность больше, чем способности языков, но для меня это правильный показатель прямо сейчас, поскольку то, что решит, что я буду использовать, зависит от того, смогу ли я сделать это работает или нет.
tl; dr: Я понимаю, что мой код Repa выше может быть глупым или патологическим, но это лучшее, что я могу сделать прямо сейчас. Я хотел бы иметь возможность писать лучший код на Haskell, и я надеюсь, что вы можете помочь мне в этом направлении (Донс уже сделал).:)
function archimedes_simple()
particles = [0 0 0]';
a = 4;
step = 0.1;
xrange = [-10:step:10];
yrange = [-10:step:10];
zrange = [-10:step:10];
[X,Y,Z] = ndgrid(xrange,yrange,zrange);
dists2 = bsxfun(@minus,X,particles(1)).^2+ ...
bsxfun(@minus,Y,particles(2)).^2+ ...
bsxfun(@minus,Z,particles(3)).^2;
inside = dists2 < a^2;
num_inside = sum(inside(:));
disp('');
disp(['Step = ' num2str(step)]);
disp(['Volume of individual particles = ' num2str(size(particles,2)*4*pi*a^3/3)]);
disp(['Volume of cubes inside particles = ' num2str(step^3*num_inside)]);
end
Редактировать 2: Новая, более быстрая и простая версия кода Repa
Теперь я немного больше прочитал о Repa и немного подумал. Ниже новая версия Repa. В этом случае я создаю координаты x, y и z как трехмерные массивы, используя функцию расширения Repa, из списка значений (аналогично тому, как ndgrid работает в Matlab). Затем я сопоставляю эти массивы, чтобы вычислить расстояние до сферической частицы. Наконец, я складываю полученную трехмерную матрицу расстояний, подсчитываю, сколько координат находится внутри сферы, а затем умножаю ее на постоянный коэффициент, чтобы получить приблизительный объем. Моя реализация алгоритма теперь намного больше похожа на вышеприведенную версию Matlab, и больше нет преобразования в вектор.
Новая версия запускается на моем компьютере примерно за 5 секунд, что является значительным улучшением по сравнению с предыдущим. Синхронизация будет такой же, если я использую "многопоточный" во время компиляции, в сочетании с "+RTS -N2" или нет, но многопоточная версия максимально использует оба ядра моего компьютера. Однако я видел несколько капель "-N2" до 3,1 секунды, но потом не смог воспроизвести их. Может быть, он очень чувствителен к другим процессам, запущенным одновременно? Я закрыл большинство программ на своем компьютере при тестировании, но некоторые программы все еще работают, например фоновые процессы.
Если мы используем "-N2" и добавляем переключатель времени выполнения для выключения параллельного GC (-qg), время постоянно уменьшается до ~4,1 секунды, и используется -qa для "использования ОС для установки сходства потоков (экспериментального)", время было сокращено до ~3,5 секунд. Если посмотреть на результат работы программы с "+RTS -s", то гораздо меньше GC выполняется с использованием -qg.
Сегодня днем я посмотрю, смогу ли я запустить код на 8-ядерном компьютере, просто для удовольствия.:)
import Data.Array.Repa as R
import Prelude as P
import qualified Data.List as L
-- Calculate the volume of a spherical particle by putting it in a bath of coordinates. Generate coordinates (x,y,z) in a cuboid. Then, for each coordinate, check if it is inside the sphere. Sum those coordinates and multiply by the coordinate grid step size to find an approximate volume.
particles :: [(Double,Double,Double)]
particles = [(0,0,0)]
-- Radius of the spherical particle
a = 4
volume_individuals = fromIntegral (length particles) * 4*pi*a^3/3
-- Generate the coordinates.
step = 0.1
coords_list = [-10,-10+step..10] :: [Double]
num_coords = (length coords_list) :: Int
coords :: Array DIM1 Double
coords = fromList (Z :. (num_coords ::Int)) coords_list
coords_slice :: Array DIM1 Double
coords_slice = slice coords (Z :. All)
-- x, y and z are 3-D arrays, where the same index into each array can be used to find a single coordinate, e.g. (x(i,j,k),y(i,j,k),z(i,j,k)).
x,y,z :: Array DIM3 Double
x = extend (Z :. All :. num_coords :. num_coords) coords_slice
y = extend (Z :. num_coords :. All :. num_coords) coords_slice
z = extend (Z :. num_coords :. num_coords :. All) coords_slice
-- Calculate the squared distance from each coordinate to the center of the spherical particle.
dist2 :: (Double, Double, Double) -> Array DIM3 Double
dist2 particle = ((R.map (squared_diff xp) x) + (R.map (squared_diff yp) y) + (R.map ( squared_diff zp) z))
where
(xp,yp,zp) = particle
squared_diff xi xa = (xa-xi)^2
-- Count how many of the coordinates are within the spherical particle.
num_inside_particle :: (Double,Double,Double) -> Double
num_inside_particle particle = foldAll (\acc x -> if x<a^2 then acc+1 else acc) 0 (force $ dist2 particle)
-- Calculate the approximate volume covered by the spherical particle.
volume_inside :: [Double]
volume_inside = P.map ((*step^3) . num_inside_particle) particles
main = do
putStrLn $ "Step = " P.++ show step
putStrLn $ "Volume of individual particles = " P.++ show volume_individuals
putStrLn $ "Volume of cubes inside each particle (repa) = " P.++ (P.concat . ( L.intersperse ", ") . P.map show) volume_inside
-- As an alternative, y and z could be generated from x, but this was slightly slower in my tests (~0.4 s).
--y = permute_dims_3D x
--z = permute_dims_3D y
-- Permute the dimensions in a 3-D array, (forward, cyclically)
permute_dims_3D a = backpermute (swap e) swap a
where
e = extent a
swap (Z :. i:. j :. k) = Z :. k :. i :. j
Пространственное профилирование для нового кода
Те же типы профилей, что и Дон Стюарт, сделал ниже, но для нового кода Repa.
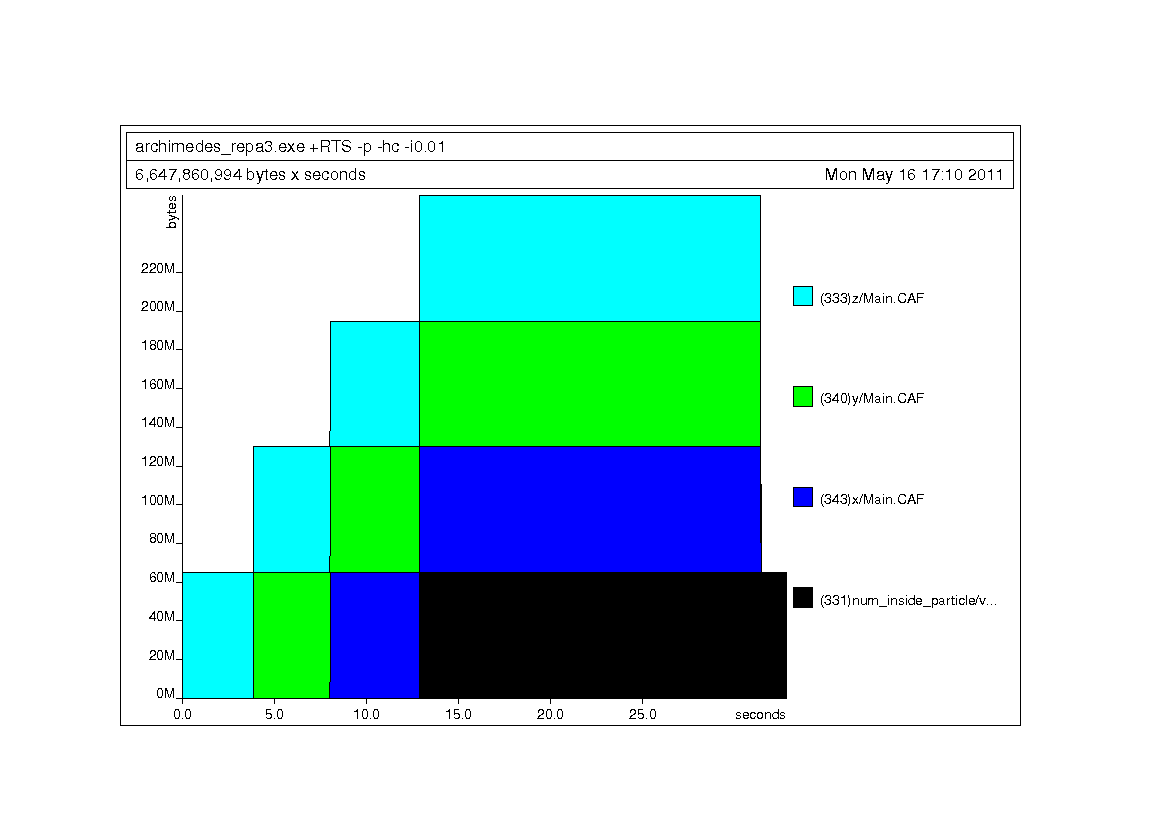
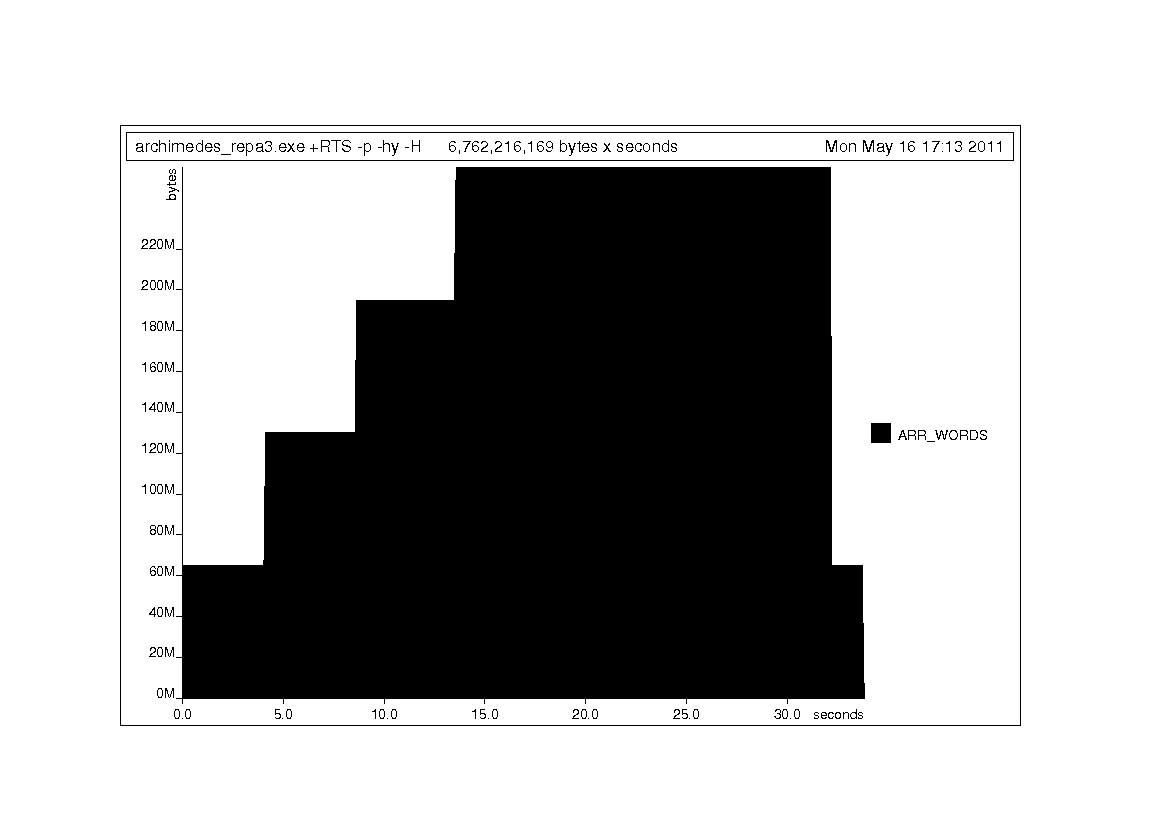
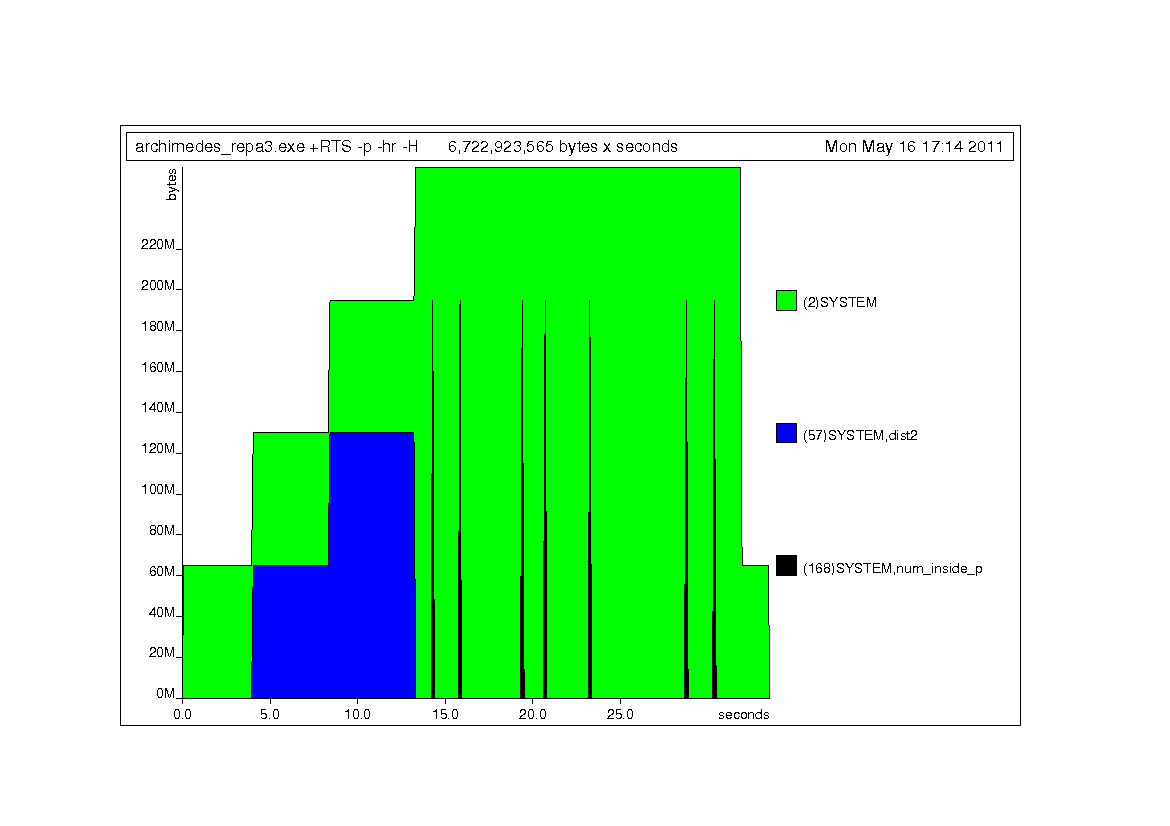
3 ответа
Комментарии к обзору кода
- 47,8% вашего времени проведено в GC.
- 1.5G выделено на кучу (!)
- Код repa выглядит намного сложнее, чем код list.
- Много параллельных GC происходит
- Я могу получить до 300% эффективности на машине -N4
- Добавление большего количества типовых подписей облегчит анализ...
rsizeне используется (выглядит дорого!)- Вы конвертируете массивы репы в векторы, почему?
- Все ваши использования
(**)можно заменить на более дешевый(^)наInt, - Есть подозрительное количество больших, постоянных списков. Все они должны быть преобразованы в массивы - это кажется дорогим.
any (==True)такой же какor
Время профилирования
COST CENTRE MODULE %time %alloc
squared_diff Main 25.0 27.3
insideParticle Main 13.8 15.3
sum_squared_diff Main 9.8 5.6
rcoords Main 7.4 5.6
particle_extended Main 6.8 9.0
particle_slice Main 5.0 7.6
insideParticles Main 5.0 4.4
yslice Main 3.6 3.0
xslice Main 3.0 3.0
ssd_vec Main 2.8 2.1
**^ Main 2.6 1.4
показывает, что ваша функция squared_diff немного подозрительно
squared_diff :: Array DIM2 Double
squared_diff = deepSeqArrays [rcoords,particle_extended]
((force2 rcoords) -^ (force2 particle_extended)) **^ 2
хотя я не вижу очевидного решения.
Космическое профилирование
Ничего особенного в профиле пространства: вы четко видите фазу списка, а затем векторную фазу. Фаза списка выделяет много, что восстанавливается.
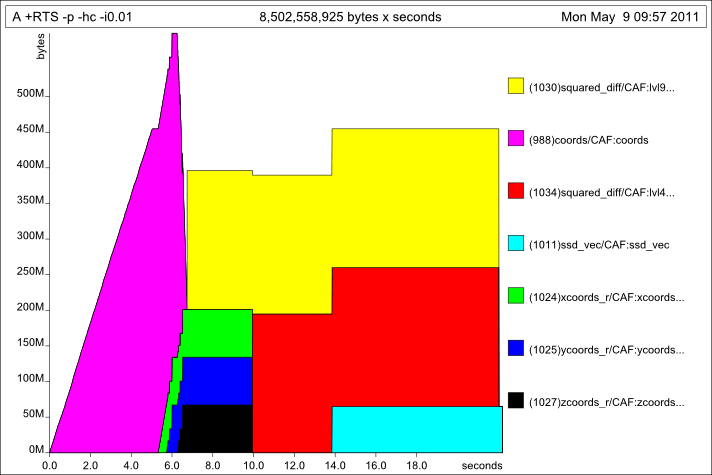
Разбивая кучу по типам, мы видим, что сначала выделяется много списков и кортежей (по запросу), затем выделяется и удерживается большой кусок массивов:
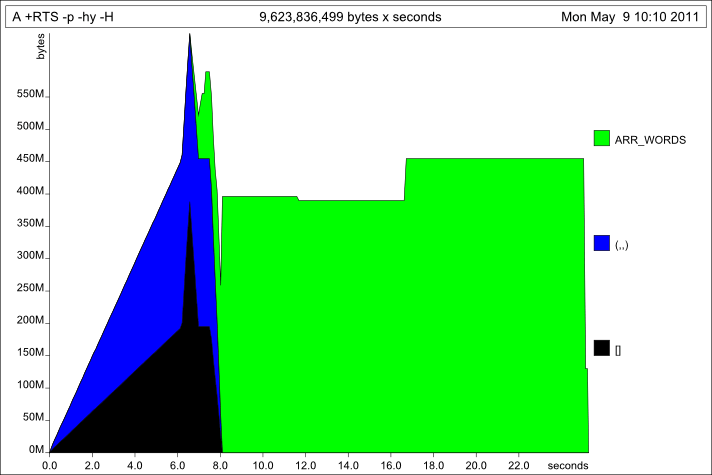
Опять же, что-то вроде того, что мы ожидали увидеть... материал массива не выделяет особенно больше, чем код списка (на самом деле, немного меньше в целом), но он просто выполняется намного дольше.
Проверка на наличие утечек в пространстве с профилированием фиксатора:
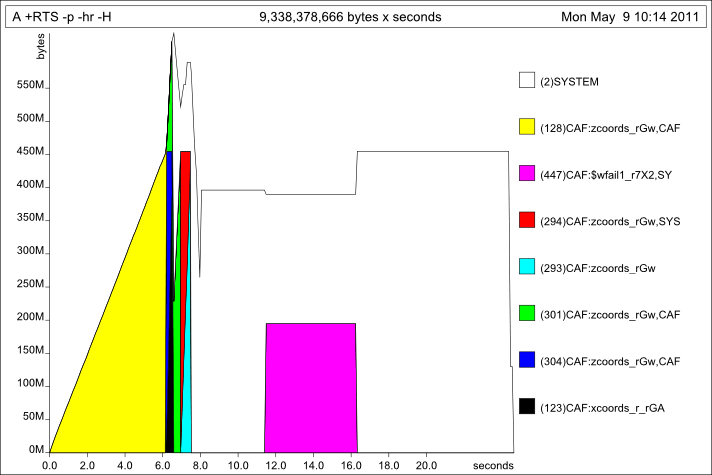
Там есть несколько интересных вещей, но ничего удивительного. zcoords сохраняется для длины выполнения программы списка, затем некоторые массивы (SYSTEM) выделяются для запуска репа.
Осмотр Ядра
Итак, на данный момент я предполагаю, что вы действительно реализовали одни и те же алгоритмы в списках и массивах (т.е. в случае массива не выполняется дополнительная работа), и нет очевидной утечки пространства. Так что мое подозрение - плохо оптимизированный код репы. Давайте посмотрим на ядро (с ghc-core.
- Код на основе списка выглядит хорошо.
- Код массива выглядит разумным (то есть появляются неупакованные примитивы), но очень сложным, и его много.
Подкладка всех CAF
Я добавил встроенные прагмы ко всем определениям массивов верхнего уровня в надежде удалить некоторые из CAf и заставить GHC оптимизировать код массива немного сложнее. Это действительно заставило GHC изо всех сил скомпилировать модуль (выделяя до 4,3 ГБ и 10 минут при работе над ним). Это подсказка для меня, что GHC не смог оптимизировать эту программу раньше, так как есть новые вещи, которые я должен сделать, когда я увеличу пороги.
действия
- Использование -H может уменьшить время, проведенное в GC.
- Попробуйте исключить преобразования из списков в репы в векторы.
- Все эти CAF (константные структуры данных верхнего уровня) выглядят довольно странно - настоящая программа не была бы списком констант верхнего уровня - на самом деле, этот модуль патологически, так что многие значения сохраняются в течение длительных периодов, вместо того, чтобы быть оптимизирован. Плавающие локальные определения внутрь.
- Обратитесь за помощью к Бену Липпмайеру, автору Repa, особенно с учетом того, что происходят некоторые интересные вещи по оптимизации.
Я изменил код, чтобы заставить rcoords а также particle_extendedи обнаружили, что мы теряем львиную долю времени внутри них напрямую:
COST CENTRE MODULE %time %alloc
rcoords Main 32.6 34.4
particle_extended Main 21.5 27.2
**^ Main 9.8 12.7
Самым большим улучшением этого кода, очевидно, было бы создание этих двух постоянных входов лучшим способом.
Обратите внимание, что это в основном ленивый потоковый алгоритм, и когда вы теряете время, это непомерная стоимость выделения как минимум двух массивов из 24361803 элементов за один раз, а затем, вероятно, выделения как минимум один или два раза больше или прекращения совместного использования., Я думаю, что лучшим вариантом для этого кода, с очень хорошим оптимизатором и правилами перезаписи zillion, будет примерное соответствие версии списка (которая также может очень легко распараллеливаться).
Я думаю, что Донс прав, что Ben & Co. будет заинтересован в этом бенчмарке, но мое подавляющее подозрение заключается в том, что это не очень хороший вариант использования для библиотеки строгих массивов, и я подозреваю, что Matlab скрывает некоторые умные оптимизации за его ngrid функция (я предоставлю оптимизацию, которую было бы полезно перенести в repa).]
Редактировать:
Вот быстрый и грязный способ распараллелить код списка. Импортировать Control.Parallel.Strategies а потом написать numberInsideParticles как:
numberInsideParticles particles coords = length $ filter id $
withStrategy (parListChunk 2000 rseq) $ P.map (insideParticles particles) coords
Это показывает хорошее ускорение при увеличении количества ядер (от 12 с на одно ядро до 3,7 с на 8), но накладные расходы на создание искры означают, что даже с 8 ядрами мы сопоставляем только одноядерную непараллельную версию. Я попробовал несколько альтернативных стратегий и получил аналогичные результаты. Опять же, я не уверен, насколько лучше мы можем сделать, чем однопотоковую версию списка здесь. Поскольку вычисления для каждой отдельной частицы настолько дешевы, мы в основном подчеркиваем распределение, а не вычисления. Я полагаю, что большой победой в таких вещах было бы векторизованное вычисление больше всего на свете, и, насколько я знаю, это в значительной степени требует ручного кодирования.
Также обратите внимание, что параллельная версия тратит примерно 70% своего времени в GC, в то время как одноядерная версия проводит там 1% своего времени (т. Е. Распределение, насколько это возможно, эффективно слито).
Я добавил несколько советов о том, как оптимизировать программы Repa в вики Haskell: http://www.haskell.org/haskellwiki/Numeric_Haskell:_A_Repa_Tutorial