Итерировать функцию по r

Question

Я новичок в R, но очень хочу "учиться на практике", поэтому прошу прощения за мой простой вопрос.

У меня есть следующий код:

MC <- function(PV, t,...){
    i <- rnorm(1, .056, .01)
    FV <- PV*exp(i*t)
    r <- log(FV/PV)
}
MC(1,1)

Мне нужно многократно перебирать функцию, давая много разных значений для r. Затем мне нужно найти стандартное отклонение всех результатов (возможно, вывести их на гистограмму?). Я пытался писать циклы, используя онлайн-руководства, но, похоже, не могу найти ничего конкретного для моей проблемы. Мне всегда кажется, что я в конечном итоге создаю бесконечный цикл, и я не могу написать команду разрыва, которая работает.

Я уверен, что есть кое-что основное, что я пропускаю, но для моей жизни я, кажется, не могу решить это.

Answer 1

Для начала, ваша функция должна что-то возвращать. Сейчас он устанавливает значение для переменной в среде, к которой у вас нет доступа. Я бы предложил:

MC <- function(PV, t,...){
  i <- rnorm(1, .056, .01)
  FV <- PV*exp(i*t)
  log(FV/PV)
}

replicate() Функция была разработана для многократной оценки стохастической функции с одними и теми же входами. Вот, сделайте:

set.seed(123)
# how about 100 trials?
replicate(100, MC(1,1))
  [1] 0.05039524 0.05369823 0.07158708 0.05670508 0.05729288 0.07315065 0.06060916
  [8] 0.04334939 0.04913147 0.05154338 0.06824082 0.05959814 0.06000771 0.05710683
 [15] 0.05044159 0.07386913 0.06097850 0.03633383 0.06301356 0.05127209 0.04532176
 [22] 0.05382025 0.04573996 0.04871109 0.04974961 0.03913307 0.06437787 0.05753373
 [29] 0.04461863 0.06853815 0.06026464 0.05304929 0.06495126 0.06478133 0.06421581
 [36] 0.06288640 0.06153918 0.05538088 0.05294037 0.05219529 0.04905293 0.05392083
 [43] 0.04334604 0.07768956 0.06807962 0.04476891 0.05197115 0.05133345 0.06379965
 [50] 0.05516631 0.05853319 0.05571453 0.05557130 0.06968602 0.05374229 0.07116471
 [57] 0.04051247 0.06184614 0.05723854 0.05815942 0.05979639 0.05097677 0.05266793
 [64] 0.04581425 0.04528209 0.05903529 0.06048210 0.05653004 0.06522267 0.07650085
 [71] 0.05108969 0.03290831 0.06605739 0.04890799 0.04911991 0.06625571 0.05315227
 [78] 0.04379282 0.05781303 0.05461109 0.05605764 0.05985280 0.05229340 0.06244377
 [85] 0.05379513 0.05931782 0.06696839 0.06035181 0.05274068 0.06748808 0.06593504
 [92] 0.06148397 0.05838732 0.04972094 0.06960652 0.04999740 0.07787333 0.07132611
 [99] 0.05364300 0.04573579

Если вся цель MC это запустить симуляцию Монте-Карло (что предполагает название), то вы можете переписать функцию, чтобы принять n аргумент при необходимости, вот так:

MC <- function(PV, t, n = 1, ...){
  i <- rnorm(n, .056, .01)
  FV <- PV*exp(i*t)
  log(FV/PV)
}
set.seed(123)
MC(1, 1, n = 100)
# With the same seed it returns the same result as above, but more efficiently

Вы могли бы тогда взять mn размер образцов и положить их в массив, используя новый MC функции, и рассчитать стандартное отклонение каждого образца, а затем построить гистограмму

m <- 100
n <- 10
set.seed(123)
samples <- replicate(m, MC(1, 1, n))
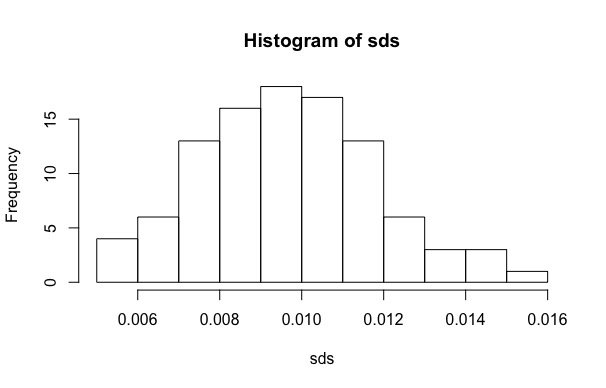
sds <- apply(samples, 2, sd)
hist(sds)

Answer 2

Вы можете выполнять итерацию (цикл) с различными значениями PV и t и возвращать значение r в функции. Используя некоторый порог для r, вы можете разорвать петлю.

MC <- function(PV, t){
  i <- rnorm(1, .056, .01)
  FV <- PV*exp(i*t)
  r <- log(FV/PV)
  print(r)
  return(r)
}

for (PV in 1:10){
  for (t in 2:9){
    th = MC(PV,t)
    if(th>0.2){
      break
    }
    }
  }