Картезианский продукт Performant (CROSS JOIN) с пандами
Изначально предполагалось, что содержимое этого поста будет частью Pandas Merging 101, но из-за характера и размера содержимого, необходимого для полной отдачи этой теме, оно было перенесено в собственную QnA.
Учитывая два простых DataFrames;
left = pd.DataFrame({'col1' : ['A', 'B', 'C'], 'col2' : [1, 2, 3]})
right = pd.DataFrame({'col1' : ['X', 'Y', 'Z'], 'col2' : [20, 30, 50]})
left
col1 col2
0 A 1
1 B 2
2 C 3
right
col1 col2
0 X 20
1 Y 30
2 Z 50
Суммарное произведение этих фреймов может быть вычислено и будет выглядеть примерно так:
A 1 X 20
A 1 Y 30
A 1 Z 50
B 2 X 20
B 2 Y 30
B 2 Z 50
C 3 X 20
C 3 Y 30
C 3 Z 50
Каков наиболее эффективный метод вычисления этого результата?
6 ответов
Давайте начнем с установления эталона. Самый простой способ решить эту проблему - использовать временный столбец "ключ":
def cartesian_product_basic(left, right):
return (
left.assign(key=1).merge(right.assign(key=1), on='key').drop('key', 1))
cartesian_product_basic(left, right)
col1_x col2_x col1_y col2_y
0 A 1 X 20
1 A 1 Y 30
2 A 1 Z 50
3 B 2 X 20
4 B 2 Y 30
5 B 2 Z 50
6 C 3 X 20
7 C 3 Y 30
8 C 3 Z 50
Как это работает, так это то, что обоим фреймам данных назначается временный столбец "ключа" с одинаковым значением (скажем, 1). merge затем выполняет соединение "многие ко многим" для "ключа".
Хотя трюк "многие ко многим" работает для DataFrames разумного размера, вы увидите относительно более низкую производительность при работе с большими данными.
Более быстрая реализация потребует NumPy. Вот некоторые известные реализации NumPy 1-мерного декартового произведения. Мы можем использовать некоторые из этих эффективных решений, чтобы получить желаемый результат. Моя любимая, однако, первая реализация @senderle.
def cartesian_product(*arrays):
la = len(arrays)
dtype = np.result_type(*arrays)
arr = np.empty([len(a) for a in arrays] + [la], dtype=dtype)
for i, a in enumerate(np.ix_(*arrays)):
arr[...,i] = a
return arr.reshape(-1, la)
Обобщение: CROSS JOIN для уникальных или неуникальных проиндексированных фреймов данных
отказ
Эти решения оптимизированы для DataFrames с несмешанными скалярными dtypes. Если вы имеете дело со смешанными dtypes, используйте на свой страх и риск!
Этот трюк будет работать на любом виде DataFrame. Мы вычисляем декартово произведение числовых индексов DataFrames с использованием вышеупомянутых cartesian_product используйте это, чтобы переиндексировать DataFrames, и
def cartesian_product_generalized(left, right):
la, lb = len(left), len(right)
idx = cartesian_product(np.ogrid[:la], np.ogrid[:lb])
return pd.DataFrame(
np.column_stack([left.values[idx[:,0]], right.values[idx[:,1]]]))
cartesian_product_generalized(left, right)
0 1 2 3
0 A 1 X 20
1 A 1 Y 30
2 A 1 Z 50
3 B 2 X 20
4 B 2 Y 30
5 B 2 Z 50
6 C 3 X 20
7 C 3 Y 30
8 C 3 Z 50
np.array_equal(cartesian_product_generalized(left, right),
cartesian_product_basic(left, right))
True
И, по аналогии,
left2 = left.copy()
left2.index = ['s1', 's2', 's1']
right2 = right.copy()
right2.index = ['x', 'y', 'y']
left2
col1 col2
s1 A 1
s2 B 2
s1 C 3
right2
col1 col2
x X 20
y Y 30
y Z 50
np.array_equal(cartesian_product_generalized(left, right),
cartesian_product_basic(left2, right2))
True
Это решение может распространяться на несколько фреймов данных. Например,
def cartesian_product_multi(*dfs):
idx = cartesian_product(*[np.ogrid[:len(df)] for df in dfs])
return pd.DataFrame(
np.column_stack([df.values[idx[:,i]] for i,df in enumerate(dfs)]))
cartesian_product_multi(*[left, right, left]).head()
0 1 2 3 4 5
0 A 1 X 20 A 1
1 A 1 X 20 B 2
2 A 1 X 20 C 3
3 A 1 X 20 D 4
4 A 1 Y 30 A 1
Дальнейшее упрощение
Более простое решение без участия @senderle's cartesian_product возможно при работе только с двумя DataFrames. С помощью np.broadcast_arraysМы можем достичь почти такого же уровня производительности.
def cartesian_product_simplified(left, right):
la, lb = len(left), len(right)
ia2, ib2 = np.broadcast_arrays(*np.ogrid[:la,:lb])
return pd.DataFrame(
np.column_stack([left.values[ia2.ravel()], right.values[ib2.ravel()]]))
np.array_equal(cartesian_product_simplified(left, right),
cartesian_product_basic(left2, right2))
True
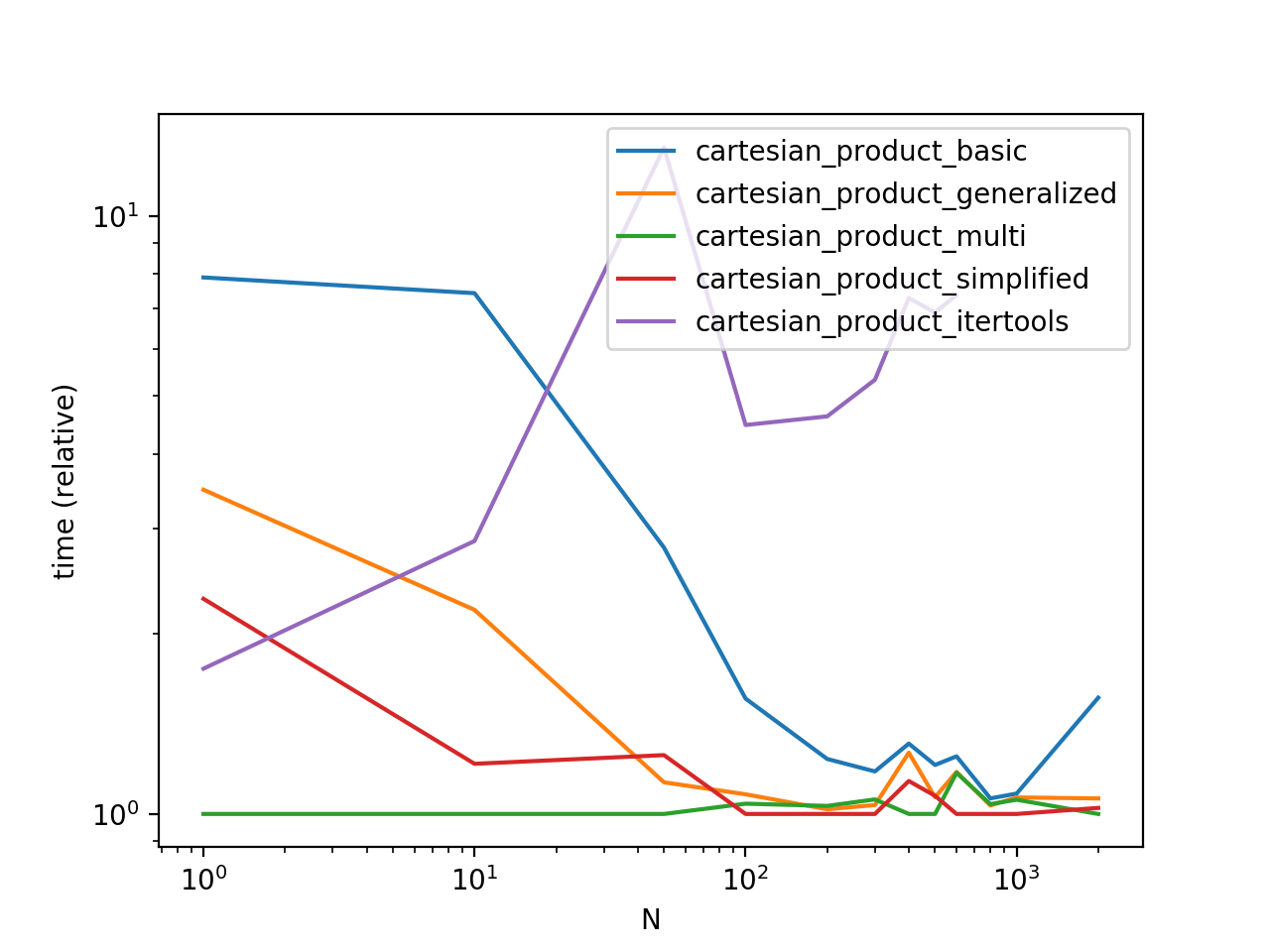
Сравнение производительности
Сравнивая эти решения на некоторых надуманных фреймах данных с уникальными индексами, мы имеем
Обратите внимание, что время может варьироваться в зависимости от ваших настроек, данных и выбора cartesian_product вспомогательная функция, если применимо.
Функции из других ответов
# Wen's answer: https://stackru.com/a/53699198/4909087
# I've put my own spin on this to make it as fast as possible.
def cartesian_product_itertools(left, right):
return pd.DataFrame([
[*x, *y] for x, y in itertools.product(
left.values.tolist(), right.values.tolist())])
Код производительности производительности
Это временный скрипт. Все вызываемые здесь функции определены выше.
from timeit import timeit
import pandas as pd
import matplotlib.pyplot as plt
res = pd.DataFrame(
index=['cartesian_product_basic', 'cartesian_product_generalized',
'cartesian_product_multi', 'cartesian_product_simplified',
'cartesian_product_itertools'],
columns=[1, 10, 50, 100, 200, 300, 400, 500, 600, 800, 1000, 2000],
dtype=float
)
for f in res.index:
for c in res.columns:
# print(f,c)
if f in {'cartesian_product_itertools'} and c > 600:
continue
left2 = pd.concat([left] * c, ignore_index=True)
right2 = pd.concat([right] * c, ignore_index=True)
stmt = '{}(left2, right2)'.format(f)
setp = 'from __main__ import left2, right2, {}'.format(f)
res.at[f, c] = timeit(stmt, setp, number=5)
ax = res.div(res.min()).T.plot(loglog=True)
ax.set_xlabel("N");
ax.set_ylabel("time (relative)");
plt.show()
С помощью itertoolsproduct и воссоздайте значение в датафрейме
import itertools
l=list(itertools.product(left.values.tolist(),right.values.tolist()))
pd.DataFrame(list(map(lambda x : sum(x,[]),l)))
0 1 2 3
0 A 1 X 20
1 A 1 Y 30
2 A 1 Z 50
3 B 2 X 20
4 B 2 Y 30
5 B 2 Z 50
6 C 3 X 20
7 C 3 Y 30
8 C 3 Z 50
Вот подход с тройным concat
m = pd.concat([pd.concat([left]*len(right)).sort_index().reset_index(drop=True),
pd.concat([right]*len(left)).reset_index(drop=True) ], 1)
col1 col2 col1 col2
0 A 1 X 20
1 A 1 Y 30
2 A 1 Z 50
3 B 2 X 20
4 B 2 Y 30
5 B 2 Z 50
6 C 3 X 20
7 C 3 Y 30
8 C 3 Z 50
h ttps://stackru.com/images/dc5d211838bce69aa47d57f72ad64b4539f9dccf.png
Один из вариантов — с expand_grid от pyjanitor :
# pip install pyjanitor
import pandas as pd
import janitor as jn
others = {'left':left, 'right':right}
jn.expand_grid(others = others)
left right
col1 col2 col1 col2
0 A 1 X 20
1 A 1 Y 30
2 A 1 Z 50
3 B 2 X 20
4 B 2 Y 30
5 B 2 Z 50
6 C 3 X 20
7 C 3 Y 30
8 C 3 Z 50
Я думаю, что самым простым способом было бы добавить фиктивный столбец в каждый фрейм данных, выполнить для него внутреннее слияние, а затем удалить этот фиктивный столбец из полученного декартова фрейма данных:
left['dummy'] = 'a'
right['dummy'] = 'a'
cartesian = left.merge(right, how='inner', on='dummy')
del cartesian['dummy']
продукт = (
df1.assign(key=1)
.merge(df2.assign(key=1), on="key")
.drop("key", axis=1)
)