Как карта / анимация числа на основе динамической кривой

Question

Мне действительно не хватает терминологии здесь, поэтому любая помощь с этим ценю. Даже если он не отвечает на вопрос, он может помочь мне приблизиться к ответу.

Как я могу получить y от функции p где извилистость также является переменной (возможно между 0 и 1? Или как лучше?).

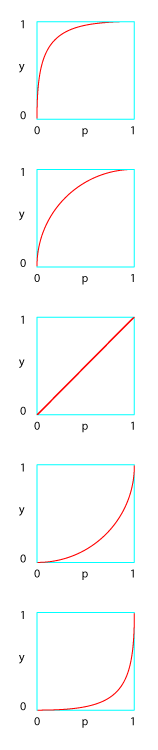
Я предполагаю p всегда между 1 и 0, как и выход y,
Графика - просто иллюстрация, мне не нужна эта точная кривая, но что-то близко к этой идее.

Псевдокод достаточно хорош как ответ или что-то в стиле c (c, javascript и т. Д.).

Чтобы дать небольшой контекст, у меня есть функция отображения, где один параметр может быть - то, что я назвал - функция ослабления. Там основаны на уравнениях Пеннера. Так, например, если бы я хотел сделать easyIn, я бы предоставил:

 function (p) { return p * p; };

Но я бы хотел иметь возможность делать то, что изображено на картинках: динамически менять легкость. С такой функцией, как:

function (p, curviness) { return /* something */; }

Answer 1

Вы можете попробовать поиграть с Суперэллипсом, который, кажется, имеет искомую форму. (Особый случай: Squircle)

Обновить

Итак, уравнение для суперэллипса выглядит следующим образом:

abs(x/a)^n + abs(y/b)^n = 1

Вы будете работать в диапазоне от [0,1] в обоих случаях, поэтому мы можем отбросить абсолютные значения.

a а также b для большой и малой осей эллипса; мы собираемся установить их равными 1 (чтобы суперэллипс растягивался только до +/-1 в любом направлении) и смотрел только на первый квадрант (снова [0, 1]).

Это оставляет нас с:

x^n + y^n = 1

Вы хотите, чтобы ваша конечная функция выглядела примерно так:

y = f(p, n)

поэтому нам нужно привести вещи в эту форму (решите для у).

Ваша первоначальная мысль о том, что делать дальше, была правильной (но переменные были переключены):

y^n = 1 - p^n

подставляя вашу переменную p за x,

Теперь, изначально я думал о попытке использовать log изолировать y, но это будет означать, что мы должны принять log_y с обеих сторон, которые бы не изолировали его. Вместо этого мы можем взять n-й корень, чтобы отменить n таким образом изолируя y:

y = nthRoot(n, 1 - p^n)

Если это сбивает с толку, то это может помочь: квадратный корень просто возводит в степень 1/2 так что если вы взяли квадратный корень из x у вас будет:

sqrt(x) == x^(1/2)

и что мы сделали, это взяли n-й корень, что означает, что мы подняли вещи до 1/n власть, которая отменяет n сила y с тех пор, как вы их умножите:

(y^n)^(1/n) == y^(n * 1/n) == y^1 == y

Таким образом, мы можем написать вещи как

y = (1 - p^n)^(1/n)

чтобы вещи выглядели лучше.

Итак, теперь у нас есть уравнение в виде

y = f(p, n)

но мы еще не закончили: это уравнение работало со значениями в первом квадранте суперэллипса; график этого квадранта выглядит иначе, чем вы хотели - вы хотели, чтобы то, что появилось во втором квадранте, только смещено.

Мы можем исправить это, перевернув граф в первом квадранте. Мы сделаем это, вычтя это из 1. Таким образом, окончательное уравнение будет:

y = 1 - (1 - p^n)^(1/n)

который прекрасно работает по расчетам моего TI-83.

Примечание: в статье в Википедии говорится, что когда n находится между 0 а также 1 тогда кривая будет изгибаться, когда n равно 1 вы получаете прямую линию, и когда n больше, чем 1 тогда он будет изгнан. Тем не менее, так как мы вычитаем вещи из 1, это поведение полностью изменено! (Так 0 через 1 означает, что он выгнут, и больше, чем 1 означает, что он поклонился).

И вот у вас это есть - надеюсь, это то, что вы искали:)

Answer 2

Ваш curviness свойство является показателем

function(p, exp) { return Math.pow(p, exp); }

• exp = 1 дает вам прямую линию
• exp > 1 дает вам экспоненциальные линии (два нижних)
• 0 < exp < 1 дает вам логарифмические строки (две верхние)

Чтобы получить "соответствующую" кривизну выше и ниже, exp = 2 будет соответствовать exp = 1/2 через линейную разделительную линию, чтобы вы могли определить функцию "изогнутости", которая делает ее более интуитивно понятной для вас.

function curvyInterpolator(p, curviness) {
    curviness = curviness > 0 ? curviness : 1/(-curviness);
    return Math.pow(p, curviness);
}