Какова будет временная сложность следующего рекурсивного алгоритма?

Question

Какова будет сложность следующего рекурсивного алгоритма?

void rec(n){
 if(n<=0)
    return;
 else
    rec(n/3)+rec(n/2); 
}

Answer 1

Временная сложность вышеуказанной программы O(2 ^ k) где k - глубина рекурсии. Вот, 2 возникает из-за того, что в каждом рекурсивном вызове мы выполняем вызовы на 2 других рекурсивных вызова. Теперь давайте проанализируем самую глубокую глубину рекурсии (k).

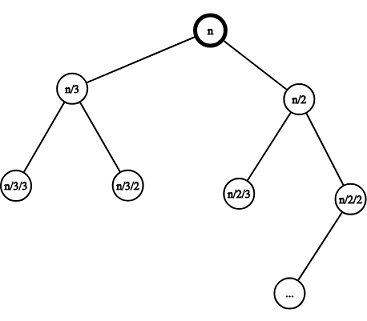
На рисунке выше, для рекурсивного пути, деленного на 2 на каждом шаге, потребуется больше времени, чтобы достичь значения меньше 1 (что является базовым случаем), и, следовательно, это будет самая глубокая глубина рекурсии. Так как, каждый раз, когда мы делим n от 2, Это займет шаги журнала, чтобы достичь менее 1, Хотя мы также разделяем n от 3, Разделив n от 2 займет больше времени и, следовательно, ответственен как решающий фактор для самой глубокой рекурсии. Для деталей:

В 1st вызов, мы уменьшаем п на п / 2.
В 2nd вызов, мы уменьшаем п на (п / 2) / 2 = п / 4 = п / 2^2.
Следовательно, в Kth шаг, мы уменьшаем n на: n / 2^k = 1.
Итак, n = 2 ^ k.

Взяв бревно 2 с обеих сторон,

log2 n = log2 (2 ^ k)
log2 n = k log2(2)
log2 n = k * 1 [поскольку log2(2) равно 1 ]

Поэтому в самой глубокой рекурсии нам нужно k = log(n) шаги для достижения n = 1 и еще один шаг для достижения n <= 0. Но в целом глубина рекурсии будет между log3 n в log2 n,

Таким образом, общая сложность времени O(2 ^ log n) в худшем случае. Но, поскольку мы также делим n от 3 и, следовательно, глубина всех рекурсивных путей, начиная с верхнего до конечного узла, не будет такой же, как у log n, Следовательно, мы можем сделать вывод о сложности времени как O(2 ^ k) где k - глубина рекурсии.