Быстрый, элегантный способ расчета эмпирической / выборочной ковариограммы

Question

Кто-нибудь знает хороший метод для расчета эмпирической / выборочной ковариограммы, если это возможно в Python?

Это скриншот книги, которая содержит хорошее определение ковариаграммы:

Если я правильно понял, для заданного лага / ширины h я должен получить все пары точек, которые разделены h (или меньше h), умножить его значения и для каждой из этих точек вычислить среднее значение, которые в этом случае определяются как m(x_i). Однако, согласно определению m(x_{i}), если я хочу вычислить m(x1), мне нужно получить среднее значение, расположенное на расстоянии h от x1. Это выглядит как очень интенсивное вычисление.

Прежде всего, я правильно понимаю? Если так, каков хороший способ вычислить это, предполагая двумерное пространство? Я пытался кодировать это на Python (используя numpy и pandas), но это занимает пару секунд, и я даже не уверен, что это правильно, поэтому я воздержусь от публикации кода здесь. Вот еще одна попытка очень наивной реализации:

from scipy.spatial.distance import pdist, squareform
distances = squareform(pdist(np.array(coordinates))) # coordinates is a nx2 array
z = np.array(z) # z are the values
cutoff = np.max(distances)/3.0 # somewhat arbitrary cutoff
width = cutoff/15.0
widths = np.arange(0, cutoff + width, width)
Z = []
Cov = []

for w in np.arange(len(widths)-1): # for each width
    # for each pairwise distance
    for i in np.arange(distances.shape[0]): 
        for j in np.arange(distances.shape[1]): 
            if distances[i, j] <= widths[w+1] and distances[i, j] > widths[w]:
                m1 = []
                m2 = []
                # when a distance is within a given width, calculate the means of
                # the points involved
                for x in np.arange(distances.shape[1]):
                    if distances[i,x] <= widths[w+1] and distances[i, x] > widths[w]:
                        m1.append(z[x])

                for y in np.arange(distances.shape[1]):
                    if distances[j,y] <= widths[w+1] and distances[j, y] > widths[w]:
                        m2.append(z[y])

                mean_m1 = np.array(m1).mean() 
                mean_m2 = np.array(m2).mean()
                Z.append(z[i]*z[j] - mean_m1*mean_m2)
    Z_mean = np.array(Z).mean() # calculate covariogram for width w
    Cov.append(Z_mean) # collect covariances for all widths

Однако теперь я подтвердил, что в моем коде есть ошибка. Я знаю это, потому что я использовал вариограмму для вычисления ковариограммы (ковариограмма (h) = ковариограмма (0) - вариограмма (h)), и я получил другой график:

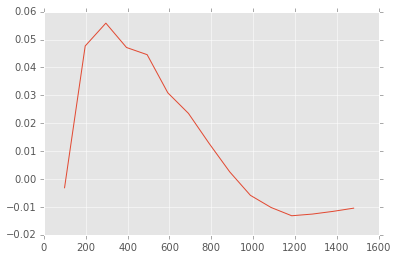
И это должно выглядеть так:

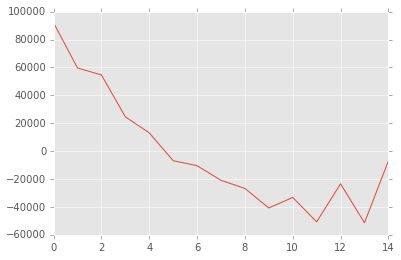
Наконец, если вы знаете библиотеку Python/R/MATLAB для расчета эмпирических ковариограмм, дайте мне знать. По крайней мере, таким образом я могу проверить, что я сделал.

Answer 1

Можно использовать scipy.cov, но если выполнить вычисления напрямую (что очень просто), есть еще несколько способов ускорить это.

Сначала создайте поддельные данные, которые имеют пространственные корреляции. Я сделаю это, сначала сделав пространственные корреляции, а затем используя случайные точки данных, которые генерируются с использованием этого, где данные располагаются в соответствии с базовой картой, а также принимают значения базовой карты.

Изменить 1:
Я изменил генератор точек данных, чтобы положения были чисто случайными, но значения z пропорциональны пространственной карте. И я изменил карту так, чтобы левая и правая стороны были смещены относительно друг друга, чтобы создать отрицательную корреляцию в целом h,

from numpy import *
import random
import matplotlib.pyplot as plt

S = 1000
N = 900
# first, make some fake data, with correlations on two spatial scales
#     density map
x = linspace(0, 2*pi, S)
sx = sin(3*x)*sin(10*x)
density = .8* abs(outer(sx, sx))
density[:,:S//2] += .2
#     make a point cloud motivated by this density
random.seed(10)  # so this can be repeated
points = []
while len(points)<N:
    v, ix, iy = random.random(), random.randint(0,S-1), random.randint(0,S-1)
    if True: #v<density[ix,iy]:
        points.append([ix, iy, density[ix,iy]])
locations = array(points).transpose()
print locations.shape
plt.imshow(density, alpha=.3, origin='lower')
plt.plot(locations[1,:], locations[0,:], '.k')
plt.xlim((0,S))
plt.ylim((0,S))
plt.show()
#     build these into the main data: all pairs into distances and z0 z1 values
L = locations
m = array([[math.sqrt((L[0,i]-L[0,j])**2+(L[1,i]-L[1,j])**2), L[2,i], L[2,j]] 
                         for i in range(N) for j in range(N) if i>j])

Который дает:

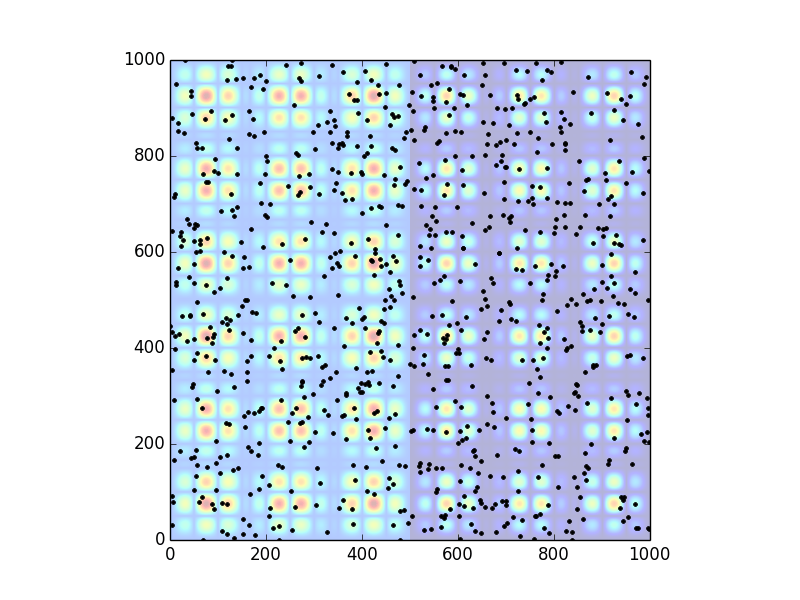
Выше приведены только симулированные данные, и я не пытался оптимизировать их производство и т. Д. Я предполагаю, что именно здесь начинается OP, с задачей, приведенной ниже, поскольку данные уже существуют в реальной ситуации.

---

Теперь вычислите "ковариограмму" (что намного проще, чем генерация поддельных данных, кстати). Идея здесь состоит в том, чтобы отсортировать все пары и связанные значения по h, а затем индексировать в них с помощью ihvals, То есть подведение итогов по индексу ihval сумма сверх N(h) в уравнении, так как это включает в себя все пары с h ниже желаемых значений.

Изменить 2:
Как предлагается в комментариях ниже, N(h) теперь только пары, которые находятся между h-dh а также h, а не все пары между 0 а также h (где dh расстояние между h -значения в ihvals - то есть, S/1000 был использован ниже).

# now do the real calculations for the covariogram
#    sort by h and give clear names
i = argsort(m[:,0])  # h sorting
h = m[i,0]
zh = m[i,1]
zsh = m[i,2]
zz = zh*zsh

hvals = linspace(0,S,1000)  # the values of h to use (S should be in the units of distance, here I just used ints)
ihvals = searchsorted(h, hvals)
result = []
for i, ihval in enumerate(ihvals[1:]):
    start, stop = ihvals[i-1], ihval
    N = stop-start
    if N>0:
        mnh = sum(zh[start:stop])/N
        mph = sum(zsh[start:stop])/N
        szz = sum(zz[start:stop])/N
        C = szz-mnh*mph
        result.append([h[ihval], C])
result = array(result)
plt.plot(result[:,0], result[:,1])
plt.grid()
plt.show()

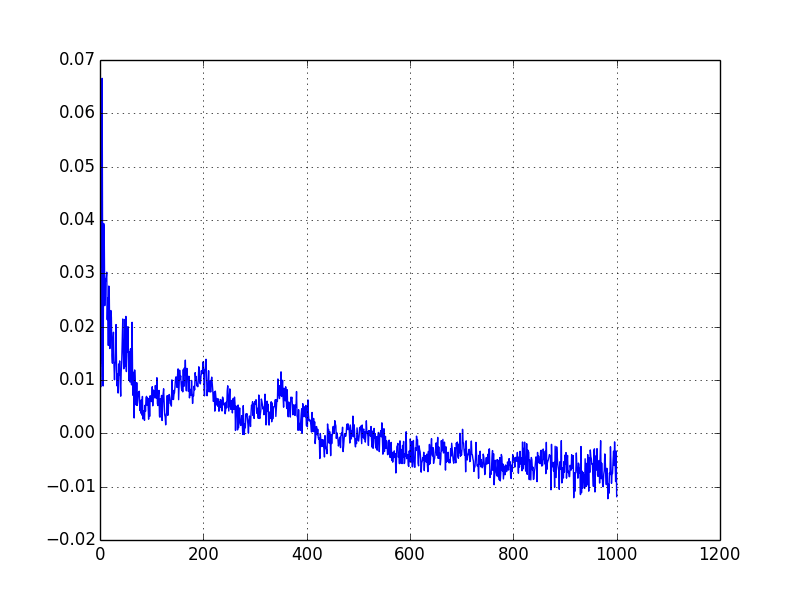
что выглядит разумно для меня, так как можно увидеть неровности или впадины при ожидаемых значениях h, но я не сделал тщательной проверки.

Основное ускорение здесь закончилось scipy.cov является то, что можно рассчитать все продукты, zz, В противном случае, один будет кормить zh а также zsh в cov за каждый новый h и все продукты будут пересчитаны. Это вычисление можно ускорить, сделав частичные суммы, т. Е. Из ihvals[n-1] в ihvals[n] на каждом шагу n Но я сомневаюсь, что это будет необходимо.