Алгоритм взаимного исключения, использующий только атомарное чтение и запись для неизвестного числа процессов и устойчивый к прерыванию процесса

Question

Я пытаюсь придумать алгоритм взаимного исключения, который основан только на атомарном чтении и атомарной записи общей памяти (т.е. без сравнения и замены или подобного).

Помимо взаимного исключения и свободы тупиков, он должен выполнять следующие свойства:

• Он должен быть устойчивым перед лицом процессов, умирающих в любой точке
• Необходимо обработать заранее неизвестное количество процессов, конкурирующих за блокировку.
• Каждые несколько секунд мне нужен один из процессов, чтобы войти в критическую секцию (мне все равно, какой)
• Он должен быть максимально эффективным для памяти
• Все мои процессы имеют разумно синхронизированный источник синхронизации (с точностью до секунды)

Я придумал способ, который выглядит для меня так, будто он может сработать, но я хотел, чтобы вы, ребята, попробовали его, чтобы посмотреть, не ошибся ли я где-нибудь или есть более элегантное решение.

Идея состоит в том, чтобы объединить модифицированную версию трехбитового алгоритма линейного ожидания Шимански (рисунок 1 на странице 4 "Пересмотренное взаимное исключение") со схемой именования процессов, основанной на общих принципах Moir и Anderson "Ожидание без ожидания", Долгожданное переименование "(M & A).

В качестве первого шага я определяю "порядок" для входящих процессов, назначая им такой идентификатор, какM & A:

M & A использует следующий мьютексный примитив (см. Рисунок 2 на странице 5):

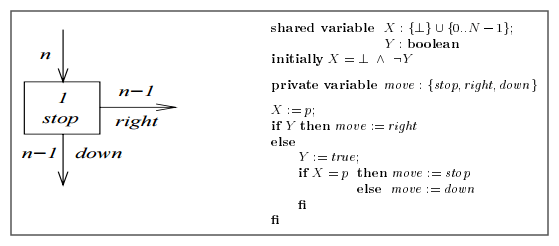
где из n процессов, входящих в блок, на этом остановится не более 1, не более n - 1сместится вправо, а не более n - 1сместится вниз.

Эти примитивы могут быть объединены в сетку, где я решил нумеровать блоки по-разному отслияний и поглощений, чтобы позволить мне вычислить номер блока, не зная общего количества блоков:

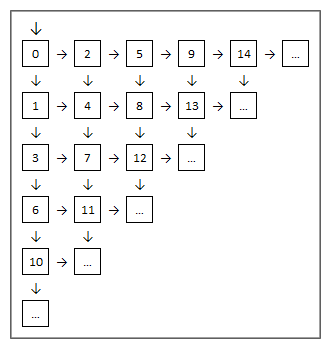
Номер ящика можно рассчитать с помощьюbox = (m*(m-1))/2 + r где m - общее количество выполненных ходов (включая перемещение в верхний левый прямоугольник, т.е. m ≥ 1), аr - количество ходов вправо (r≥ 0).

Любому новому процессу первоначально будет назначен большой глобально уникальный идентификатор (например, отметка времени + огромное случайное число), который он будет использовать в качестве значения дляp в приведенном выше алгоритме мьютекса. Затем он начнет проходить по сетке, следуя правилам примитива, начиная с верхнего левого угла, пока не остановится в каком-либо окне. Номер коробки, в которой он остановился, теперь будет новым идентификатором процесса.

Чтобы уменьшить число идентификаторов процессов (процессы могут исчезнуть; кроме того, блоки могут быть заблокированы навсегда без использования, если все входящие процессы перемещаются вправо или вниз и на этом не останавливается), я заменю логическую переменнуюY в приведенном выше примитиве. с отметкой времени.

Линия Y := trueбудет заменен наY := now где сейчас текущее время. Точно так же условие if Y then ...будет заменен наif (now - Y < timeout) then ... гдетайм-аут- это время, после которого ящик будет возвращен в доступный пул.

Пока процесс все еще выполняется, ему необходимо установить значение Y в своем блоке, чтобы оно никогда не истекло. В то время как меньшие значения времени ожидания приведут к меньшим идентификаторам и меньшему использованию памяти, теоретически он может быть выбран произвольно большим, и, таким образом, всегда должно быть возможно найти значение времени ожидания, которое будет гарантировать, что процессы никогда не потеряют свой идентификатор, если они фактически не завершат работу или умер. Значения минут, часов или даже дней должны помочь.

Теперь мы можем использовать этот порядок процессов для реализации алгоритма Шимански:

communication variables:: a, w, s: boolean = false
private variables:: j: 0..n

p1      ai=true;
p2      for(j=0;j<n;j++)
            while(sj);
p3      wi=true;
        ai=false;
p4      while(!si) {
p5          for (j=0;j<n & !aj;j++);
p6          if (j==n) {
                si=true;
p6.1            for (j=0;j<n & !aj;j++);
p6.2            if (j<n)
                    si=false;
p6.3            else {
                    wi=false;
p6.4                for(j=0;j<n;j++)
                        while(wj);
                }
            }
p7          if (j<n)
                for (j=0;j<n & (wj | !sj);j++);
p8          if (j!=i & j<n) {
p8.1            si=true;
                wi=false;
            }
        }
p9      for(j=0;j<i;j++)
            while(wj | sj);

Critical Section

e1      si=false;

Идея этого алгоритма немного сложна и для краткости (если это еще не потеряно на этом этапе), я не буду пытаться перефразировать его здесь снова ( Википедия также обсуждает вариант этого алгоритма).

Чтобы заставить этот алгоритм работать по мере необходимости (т. Е. Перед лицом прерываний процессов и неизвестного общего числа процессов), можно внести следующие изменения:

Как и Y выше, логические значения a_i, w_i и s_i будут заменены временными метками. За исключением того, что на этот раз тайм-ауты должны быть достаточно короткими, чтобы позволить критическому разделу вводиться так часто, как это необходимо, в моем случае каждые несколько секунд, так что тайм-аут 5 с может сработать. В то же время время ожидания должно быть достаточно продолжительным, чтобы оно никогда не истекло, если процесс не умирает, то есть оно должно быть длиннее, чем время наихудшего случая, которое требуется процессам для обновления временных меток для флагов, которые должны оставаться установленными.

Циклы над процессами (например, for(j=0;j<n;j++)) превратится в обход сетки идентификатора процесса сверху в порядке номеров блоков. Каждый блок может иметь 3 состояния: Никогда никого не посещал, процесс остановился в нем, или все процессы перенесены, и блок в настоящее время заблокирован. Нет необходимости проводить различие между последними двумя, поскольку заблокированный блок будет просто соответствовать процессу, который в настоящее время не пытается войти в критическую секцию (то есть a_i, w_i и s_i имеют значение false/ expired). Цикл начинается в блоке 0. Если он сталкивается с блоком, который был посещен (то есть установлено его значение X), он добавляет соседние блоки в свой "список проверки" (т. Е. Если блок 8 виден, блок 12 и 13 будут добавлены в список). Цикл завершается, когда "список проверок" полностью обработан (если, конечно, нет другого условия остановки, которое срабатывает первым (например, j < i или же & !aj)).

Теперь к моим вопросам:

1. Похоже, это будет работать надежно?
   Я никогда не делал формального доказательства такой основы. Моя интуиция (и интенсивные размышления) говорят мне, что она должна быть прочной, но я не возражаю против чего-то более строгого, чем это. Меня больше всего беспокоит влияние процесса, умирающего между p3 и e1 алгоритма Шимански, и случайного истечения флагов, в то время как другие процессы находятся в этой части кода.
2. Есть ли лучшее решение (проще / меньше ресурсов)?
   Одной из точек атаки на оптимизацию может быть тот факт, что мне не нужны все процессы, чтобы в конечном итоге попасть в критическую секцию, мне просто нужен один (и мне тоже все равно, какой).

Извините за длину этого поста и спасибо за вашу выносливость, читая его! Предложения по сокращению приветствуются...:)

PS: я также разместил этот вопрос на бирже стека CS.

Answer 1

Поскольку меня не волнует справедливость или голод (не важно, какой процесс входит в критическую секцию), мне не нужно использовать такой сложный алгоритм, как у Шимански.

Я нашел довольно красивую альтернативу: алгоритм Бернса и Линча:

program Process_i;
    type flag = (down, up);
    shared var F : array [1..N] of flag;
    var j : 1..N;
begin
    while true do begin
        1: F[i] := down;
        2: remainder;     (* remainder region *)
        3: F[i] := down;
        4: for j := 1 to i-1 do
               if F[j] = up then goto 3;
        5: F[i] := up;
        6: for j := 1 to i-1 do
               if F[j] = up then goto 3;
        7: for j := i+1 to N do
               if F[j] = up then goto 7;
        8: critical;      (* critical region *)
    end
end.

Вы можете найти его на странице 4 (836) их статьи "Взаимное исключение с использованием неделимого чтения и записи".

У него есть пара основных преимуществ:

• Это намного проще
• Он использует меньше памяти (на самом деле, они утверждают, что их алгоритм оптимален в этом отношении)
• Вся общая память имеет только одного писателя (но, конечно, несколько читателей)
• Легко превратить занятое ожидание в отложенные попытки (см. Здесь)

В сторону: идея этого алгоритма может быть визуализирована следующим образом:

Я процесс, и я стою где-то в ряд с другими людьми (все остальные процессы).
Когда я хочу войти в критический раздел, я делаю следующее:

• 3/4: Я смотрю налево и держу руку вниз, пока вижу кого-то с поднятой рукой.
• 5: Если никто слева от меня не поднял руку, я подниму свою.
• 6: я снова проверяю, поднял ли кто-нибудь слева от меня свою руку. Если так, я кладу обратно и начинаю заново. В противном случае, я держу руку вверх.
• 7: Все справа от меня идут первыми, поэтому я смотрю направо и жду, пока не увижу руки вверх.
• 8: Когда все руки справа от меня опущены, я могу войти в критическую секцию.
• 1: Когда я закончу, я положу руку обратно вниз.

Я реализовал всю идею сверху (включая M&A) с помощью этого алгоритма и в настоящее время тестирую его, и пока он кажется очень стабильным.

Реализация очень проста. На самом деле нужно было учесть только два дополнительных предостережения (если, конечно, я что-то пропустил (указатели приветствуются)):

• Если процесс доходит до строки 7 в алгоритме, он может в конечном итоге нажать goto, в этом случае, в моей реализации (см. здесь), запись в критическую секцию запрещена, и процесс пытается повторить позже. Когда повторная попытка произойдет (возможно, с большой задержкой), мне нужно обновить флаг процесса таким образом, чтобы у него не было даже самого крошечного момента, в течение которого флаг истек, или, если это произошло, мне нужно обнаружить это и перейти к строке 3 в алгоритме вместо продолжения в строке 7.
• Я добавил проверку, нужно ли вообще вводить критический раздел (т. Е. Оператор, ограничивающий скорость, с которой вводится критический раздел). Эту проверку наиболее эффективно выполнять еще до того, как процесс попытается войти в критическую секцию. Чтобы убедиться на 100%, что ни один поток не может превысить ограничение скорости, необходимо выполнить вторую проверку, когда процесс успешно войдет в критическую секцию.

Из-за общих структур данных, которые использует мой код, в настоящее время он на самом деле не находится в состоянии, которое делает его значимым для публикации здесь, но, потратив немного времени, я мог бы собрать автономную версию. Если кому-то интересно, пожалуйста, оставьте комментарий, и я сделаю это.