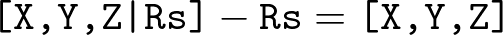Я выяснил код для проверки равных a и b в списке, но не могу понять базовую рекурсию
s(A,A).
s(A,D):- l(A,B),s(B,C),r(C,D).
l([a|A],A).
r([b|A],A).
Приведенный выше код в прологе проверяет, имеют ли заданные входные данные списка равные a и b или нет.
Такие как
s([a,a,b,b],[]).
True.
Это включает в себя рекурсию и списки различий. Может кто-нибудь объяснить, как лежащие в основе проверки рекурсии равны a и b шаг за шагом.
2 ответа
Различия в списке нелегко понять, если рассуждать о них на низком уровне.
Поэтому я сначала рекомендую более высокоуровневое представление:
За все, ваш предикат s/2 описывает список. Я говорю "описывает", потому что он не только "проверяет", но также генерирует и дополняет такие списки, если мы хотим!
Мы можем прочитать каждую цель s/2 как "а затем некоторые элементы списка".
Итак, на минуту забудем об аргументах и рассмотрим абстрактную структуру предиката. я использую (-->)/2 сейчас вместо (:-)/2 чтобы прояснить, что я говорю о небольшой вариации предиката, где я просто игнорирую аргументы:
s -> []. s -> l, s, r.
Мы можем сделать то же самое с l/2 а также r/2:
л -> [а]. r -> [b].
Это то, что предикаты описывают в абстрактном высокоуровневом представлении списков. В этой записи мне не нужно бороться со списком различий и аргументов. Вместо этого я могу сосредоточиться непосредственно на сути программы.
Очевидно, что вы можете легко перевести такой высокоуровневый код в код, который вы разместили. Фактически, Prolog выполняет этот перевод для вас, если вы обращаетесь к этому коду: он называется нотацией DCG. См. Dcg для получения дополнительной информации.
Итак, теперь понятно s//0 описывает список, который либо пуст, либо:
- список описан
l//0 - а затем список, описанный
s//0 - а затем список, описанный
r//0,
поскольку l//0 описывает список с одним элементом a, а также r//0 описывает список с одним элементом b ясно, что в списках s//0 описывает, всегда есть одинаковое количество a с и b s.
Мы используем phrase/2 вызвать DCG. Например:
? - фраза (с, Ls). Ls = []; Ls = [a, b]; Ls = [a, a, b, b]; Ls = [a, a, a, b, b, b].
Если вы начнете рассуждать о рекурсии явно, вы не добьетесь большого прогресса, потому что быстро становится слишком сложно отследить точные шаги, которые выполняет движок Prolog, и принять во внимание все возможности. Я рекомендую вам сосредоточиться на значении ваших предикатов и попытаться понять, что они на самом деле описывают.
РЕДАКТИРОВАТЬ: Если вы хотите явно рассуждать об аргументах, может помочь алгебраическая аналогия: мы можем рассматривать каждую пару аргументов как описание списка как " разницу " между двумя списками, разницу между списками, также по аналогии с дифференциалом, используемым в исчисление.
Например, "разница" между [X,Y,Z|Rs] а также Rs является [X,Y,Z], Следовательно, хотя бы символически, мы можем написать:
Обозначим через L, L 0, L 1 и L 2 списки, которые описываются такими различиями во втором пункте:
Алгебраически мы можем думать о L как о " сумме " (объединении) других списков:
Для других списков у нас есть:
Итак, в сумме имеем:
Обратите внимание, что для понимания этого не требуется рекурсия. Вместо этого важна скорее связь между аргументами. Лично я также нахожу такой вывод менее полезным, чем обратное: я думаю, что гораздо важнее заметить этот паттерн при написании такого кода, потому что это означает, что вы можете вместо этого использовать нотацию DCG и значительно сократить количество аргументов, которые передаются вокруг!
s( A, A). % s(0).
s( A, D) :- % s(n):-
l(A, B), % before,
s(B, C), % s(n-1),
r( C, D). % after.
l( [a | A],
A ).
r( [b | B],
B ).
вместе определим
%% 1
s( [a , b | B1], B1):-
l([a | A1],
A1 ),
s( A1, %s0%
A1 ), %s0%
r( [b | B1],
B1 ).
а также
%% 2
s( [a , a , b , b | B2], B2):-
l([a | A2],
A2 ),
l([a | A1], %s1%
A1 ), %s1%
s( A1, %s0% %s1%
A1 ), %s0% %s1%
r( [b | B1], %s1%
B1 ), %s1%
r( [b | B2],
B2 ).
а также
%% 3
s( [a , a , a , b , b , b | B3], B3):-
l([a | A3],
A3 ),
l([a | A2], %s2%
A2 ), %s2%
l([a | A1], %s1% %s2%
A1 ), %s1% %s2%
s( A1, %s0% %s1% %s2%
A1 ), %s0% %s1% %s2%
r( [b | B1], %s1% %s2%
B1 ), %s1% %s2%
r( [b | B2], %s2%
B2 ), %s2%
r( [b | B3],
B3 ).
и так далее и тому подобное.