Алгоритм Форда-Фулкерсона и теорема о максимальном расходе
Привет, у меня проблемы с изучением алгоритма Форда-Фулкерсона с помощью теоремы о максимальном потоке.
Согласно теореме, максимальный расход должен быть таким же, как и общий вес режущих кромок.
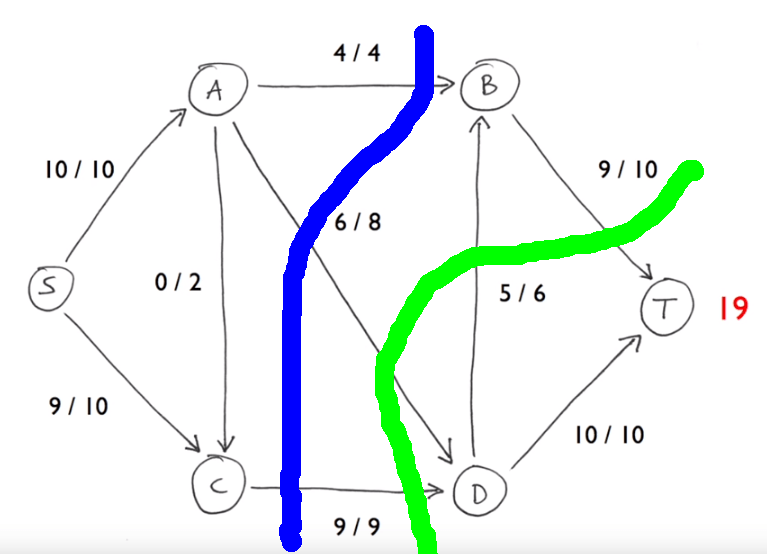
Однако просмотр видео https://www.youtube.com/watch?v=Tl90tNtKvxs вызывает у меня замешательство. Лектор говорит, что максимальный поток равен 19 по алгоритму Форда-Фулкерсона, но я не могу найти никакого сокращения с расходом 19. Что не так?
2 ответа
Нет ничего плохого в вашей интерпретации теоремы о максимальном потоке.
Минимальный набор вырезов состоит из кромок SA и CD общей емкостью 19.
Чтобы сделать разрез и рассчитать его стоимость, вы можете:
- Разделите все вершины на 2 набора, S и D, так что источник находится в S, а сток - в D.
- Обрежьте все ребра от вершины из S до вершины из D. Обратите внимание, что вам не нужно обрезать ребра, идущие от D до S.
- Сложите емкость краев, которые вы режете.
Для приведенного выше минимума S содержит вершины s и c, а D - остальные.
Разрез означает, что вы определяете разрез между источником и стоком. Этот разрез не обязательно должен быть прямой линией, кривой или любой другой формой.
Например, здесь я выбрал синий вырез, так что края AB, AD и CD проходят через разрез. Теперь, если мы посмотрим на заданный поток этих ребер и суммируем их, мы получим 4 + 6 + 9 = 19.
Альтернативный срез, например, зеленый. Здесь у нас есть ребра BT, AD и AC, которые движутся "вперед", и ребро DC, которое движется "назад". Таким образом, сумма потоков составляет 9 + 6 + 9-5 = 19. Таким образом, независимо от того, какое сокращение мы берем, сумма всегда равна 19 (конечно, нам нужно правильно вести бухгалтерский учет и вычитать потоки в обратном направлении).
Конечно, вы можете выбрать любой желаемый разрез (например, разрез сразу после источника или непосредственно перед стоком), если алгоритм выполнен правильно, то сумма всех этих разрезов всегда равна 19. Это логично, так как если поток одного среза будет больше (или меньше), чем 19, тогда наличие среза, который "продвигает" один узел с потоком 19, означает, что в этом узле поток исчез или появился.
Тем не менее, он гласит, что если вы будете выполнять итерацию по всем возможным срезам, то минимальный срез - это тот, где сумма мощностей максимизируется. Таким образом, мы можем, строго говоря, перебирать все возможные срезы и каждый раз отслеживать сумму мощностей и в конце выбирать тот, который имеет наименьший поток. Наивный подход, если бы просто повторялись все сокращения, однако привел бы к алгоритму O (2 n), который, по сравнению с алгоритмом Форда-Фулкерсона, конечно, нежелателен.