Как найти углы на изображении с помощью OpenCv
Я пытаюсь найти углы на изображении, мне не нужны контуры, только 4 угла. Я буду менять перспективу, используя 4 угла.
Я использую Opencv, но мне нужно знать шаги, чтобы найти углы и какую функцию я буду использовать.
Мои изображения будут такими:(без красных точек, я буду рисовать точки после)
Редакция:
После предложенных шагов я написал код:(Примечание: я не использую чистый OpenCv, я использую javaCV, но логика его та же).
// Load two images and allocate other structures (I´m using other image)
IplImage colored = cvLoadImage(
"res/scanteste.jpg",
CV_LOAD_IMAGE_UNCHANGED);

IplImage gray = cvCreateImage(cvGetSize(colored), IPL_DEPTH_8U, 1);
IplImage smooth = cvCreateImage(cvGetSize(colored), IPL_DEPTH_8U, 1);
//Step 1 - Convert from RGB to grayscale (cvCvtColor)
cvCvtColor(colored, gray, CV_RGB2GRAY);

//2 Smooth (cvSmooth)
cvSmooth( gray, smooth, CV_BLUR, 9, 9, 2, 2);

//3 - cvThreshold - What values?
cvThreshold(gray,gray, 155, 255, CV_THRESH_BINARY);
//4 - Detect edges (cvCanny) -What values?
int N = 7;
int aperature_size = N;
double lowThresh = 20;
double highThresh = 40;
cvCanny( gray, gray, lowThresh*N*N, highThresh*N*N, aperature_size );

//5 - Find contours (cvFindContours)
int total = 0;
CvSeq contour2 = new CvSeq(null);
CvMemStorage storage2 = cvCreateMemStorage(0);
CvMemStorage storageHull = cvCreateMemStorage(0);
total = cvFindContours(gray, storage2, contour2, Loader.sizeof(CvContour.class), CV_RETR_CCOMP, CV_CHAIN_APPROX_NONE);
if(total > 1){
while (contour2 != null && !contour2.isNull()) {
if (contour2.elem_size() > 0) {
//6 - Approximate contours with linear features (cvApproxPoly)
CvSeq points = cvApproxPoly(contour2,Loader.sizeof(CvContour.class), storage2, CV_POLY_APPROX_DP,cvContourPerimeter(contour2)*0.005, 0);
cvDrawContours(gray, points,CvScalar.BLUE, CvScalar.BLUE, -1, 1, CV_AA);
}
contour2 = contour2.h_next();
}
}
Итак, я хочу найти углы, но я не знаю, как использовать функцию углов, как cvCornerHarris и другие.
3 ответа
Во-первых, проверьте /samples/c/squares.c в вашем дистрибутиве OpenCV. В этом примере представлен квадратный детектор, и он должен стать хорошим началом для определения угловых объектов. Затем взгляните на функциональные функции OpenCV, такие как cvCornerHarris() и cvGoodFeaturesToTrack().
Вышеприведенные методы могут возвращать много угловых функций - большинство из них не будут "истинными углами", которые вы ищете. В моем приложении я должен был обнаружить квадраты, которые были повернуты или перекошены (из-за перспективы). Мой конвейер обнаружения состоял из:
- Конвертировать из RGB в оттенки серого (cvCvtColor)
- Smooth (cvSmooth)
- Порог (cvThreshold)
- Определить края (cvCanny)
- Найти контуры (cvFindContours)
- Приблизительные контуры с линейными элементами (cvApproxPoly)
- Найдите "прямоугольники", которые представляли собой структуры, которые: имели многоугольные контуры с четырьмя точками, имели достаточную площадь, смежные края составляли ~90 градусов, имели расстояние между "противоположными" вершинами достаточного размера и т. Д.
Шаг 7 был необходим, потому что слегка зашумленное изображение может дать много структур, которые выглядят прямоугольными после полигональности. В моем приложении мне также приходилось иметь дело с квадратными структурами, которые появлялись внутри или перекрывали нужный квадрат. Я обнаружил, что свойство площади контура и центр тяжести помогают определить правильный прямоугольник.
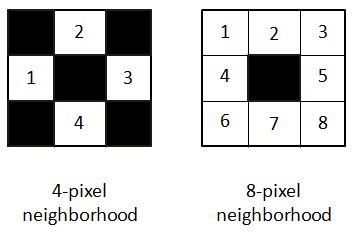
На первый взгляд, для человеческого глаза есть 4 угла. Но в компьютерном зрении угол считается точкой, в которой интенсивность градиента изменяется по всей его окрестности. Окрестность может быть 4-пиксельной или 8-пиксельной.
В уравнении, представленном для нахождения градиента интенсивности, он был рассмотрен для 4-пиксельной окрестности СМ. ДОКУМЕНТАЦИЯ.
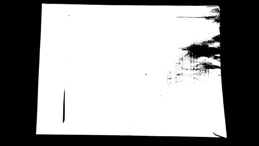
Вот мой подход к изображению, о котором идет речь. У меня также есть код на Python:
path = r'C:\Users\selwyn77\Desktop\Stack\corner'
filename = 'env.jpg'
img = cv2.imread(os.path.join(path, filename))
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY) #--- convert to grayscale
Это хороший выбор, чтобы всегда размыть изображение, чтобы удалить менее возможные изменения градиента и сохранить более интенсивные. Я решил выбрать двусторонний фильтр, который, в отличие от фильтра Гаусса, не размывает все пиксели в окрестности. Это скорее размывает пиксели, которые имеют интенсивность пикселей, аналогичную интенсивности центрального пикселя. Короче говоря, он сохраняет края / углы с высоким изменением градиента, но размывает области с минимальными изменениями градиента.
bi = cv2.bilateralFilter(gray, 5, 75, 75)
cv2.imshow('bi',bi)
Для человека это не такая большая разница по сравнению с исходным изображением. Но это имеет значение. Теперь находим возможные углы:
dst = cv2.cornerHarris(bi, 2, 3, 0.04)
dst возвращает массив (той же 2D-формы изображения) с собственными значениями, полученными из окончательного уравнения, упомянутого ЗДЕСЬ.
Теперь необходимо применить порог, чтобы выбрать эти углы за пределами определенного значения. Я буду использовать один в документации:
#--- create a black image to see where those corners occur ---
mask = np.zeros_like(gray)
#--- applying a threshold and turning those pixels above the threshold to white ---
mask[dst>0.01*dst.max()] = 255
cv2.imshow('mask', mask)
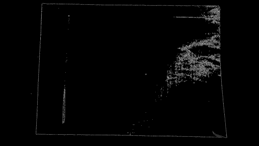
Белые пиксели - это области возможных углов. Вы можете найти много углов, соседствующих друг с другом.
Чтобы нарисовать выбранные углы на изображении:
img[dst > 0.01 * dst.max()] = [0, 0, 255] #--- [0, 0, 255] --> Red ---
cv2.imshow('dst', img)
(Пиксели красного цвета - углы, не очень заметные)
Чтобы получить массив всех пикселей с углами:
coordinates = np.argwhere(mask)
ОБНОВИТЬ
переменная coor это массив массивов. Преобразование его в список списков
coor_list = [l.tolist() for l in list(coor)]
Преобразование вышеупомянутого в список кортежей
coor_tuples = [tuple(l) for l in coor_list]
У меня есть простой и довольно наивный способ найти 4 угла. Я просто рассчитал расстояние каждого угла до каждого другого угла. Я сохранил те углы, расстояние которых превышало определенный порог.
Вот код:
thresh = 50
def distance(pt1, pt2):
(x1, y1), (x2, y2) = pt1, pt2
dist = math.sqrt( (x2 - x1)**2 + (y2 - y1)**2 )
return dist
coor_tuples_copy = coor_tuples
i = 1
for pt1 in coor_tuples:
print(' I :', i)
for pt2 in coor_tuples[i::1]:
print(pt1, pt2)
print('Distance :', distance(pt1, pt2))
if(distance(pt1, pt2) < thresh):
coor_tuples_copy.remove(pt2)
i+=1
До запуска фрагмента выше coor_tuples имел все угловые точки:[(4, 42),
(4, 43),
(5, 43),
(5, 44),
(6, 44),
(7, 219),
(133, 36),
(133, 37),
(133, 38),
(134, 37),
(135, 224),
(135, 225),
(136, 225),
(136, 226),
(137, 225),
(137, 226),
(137, 227),
(138, 226)]
После запуска фрагмента у меня осталось 4 угла:
[(4, 42), (7, 219), (133, 36), (135, 224)]
ОБНОВЛЕНИЕ 2
Теперь все, что вам нужно сделать, это просто отметить эти 4 точки на копии исходного изображения.
img2 = img.copy()
for pt in coor_tuples:
cv2.circle(img2, tuple(reversed(pt)), 3, (0, 0, 255), -1)
cv2.imshow('Image with 4 corners', img2)
Вот реализация с использованием cv2.goodFeaturesToTrack() для обнаружения углов. Подход
- Преобразовать изображение в оттенки серого
- Выполните хитрое обнаружение краев
- Обнаруживать углы
- При желании можно выполнить 4-точечное преобразование перспективы, чтобы получить вид сверху вниз.
Используя это начальное изображение,
После преобразования в оттенки серого мы выполняем точное обнаружение краев.
Теперь, когда у нас есть достойное двоичное изображение, мы можем использовать cv2.goodFeaturesToTrack()
corners = cv2.goodFeaturesToTrack(canny, 4, 0.5, 50)
В качестве параметров мы даем ему хитроумное изображение, устанавливаем максимальное количество углов 4 (maxCorners) используйте минимально допустимое качество 0,5 (qualityLevel) и установите минимально возможное евклидово расстояние между возвращаемыми углами равным 50 (minDistance). Вот результат
Теперь, когда мы определили углы, мы можем выполнить преобразование перспективы по 4 точкам, чтобы получить вид объекта сверху вниз. Сначала мы упорядочиваем точки по часовой стрелке, а затем рисуем результат на маске.
Примечание: мы могли бы просто найти контуры на изображении Canny вместо того, чтобы делать этот шаг для создания маски, но представьте, что у нас есть только 4 угловые точки для работы.
Затем мы находим контуры на этой маске и фильтруем, используя cv2.arcLength() а также cv2.approxPolyDP(). По идее, если у контура 4 точки, то это должен быть наш объект. Получив этот контур, мы выполняем перспективное преобразование.
Наконец, мы поворачиваем изображение в зависимости от желаемой ориентации. Вот результат
Код только для определения углов
import cv2
image = cv2.imread('1.png')
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 120, 255, 1)
corners = cv2.goodFeaturesToTrack(canny,4,0.5,50)
for corner in corners:
x,y = corner.ravel()
cv2.circle(image,(x,y),5,(36,255,12),-1)
cv2.imshow('canny', canny)
cv2.imshow('image', image)
cv2.waitKey()
Код для определения углов и выполнения перспективного преобразования
import cv2
import numpy as np
def rotate_image(image, angle):
# Grab the dimensions of the image and then determine the center
(h, w) = image.shape[:2]
(cX, cY) = (w / 2, h / 2)
# grab the rotation matrix (applying the negative of the
# angle to rotate clockwise), then grab the sine and cosine
# (i.e., the rotation components of the matrix)
M = cv2.getRotationMatrix2D((cX, cY), -angle, 1.0)
cos = np.abs(M[0, 0])
sin = np.abs(M[0, 1])
# Compute the new bounding dimensions of the image
nW = int((h * sin) + (w * cos))
nH = int((h * cos) + (w * sin))
# Adjust the rotation matrix to take into account translation
M[0, 2] += (nW / 2) - cX
M[1, 2] += (nH / 2) - cY
# Perform the actual rotation and return the image
return cv2.warpAffine(image, M, (nW, nH))
def order_points_clockwise(pts):
# sort the points based on their x-coordinates
xSorted = pts[np.argsort(pts[:, 0]), :]
# grab the left-most and right-most points from the sorted
# x-roodinate points
leftMost = xSorted[:2, :]
rightMost = xSorted[2:, :]
# now, sort the left-most coordinates according to their
# y-coordinates so we can grab the top-left and bottom-left
# points, respectively
leftMost = leftMost[np.argsort(leftMost[:, 1]), :]
(tl, bl) = leftMost
# now, sort the right-most coordinates according to their
# y-coordinates so we can grab the top-right and bottom-right
# points, respectively
rightMost = rightMost[np.argsort(rightMost[:, 1]), :]
(tr, br) = rightMost
# return the coordinates in top-left, top-right,
# bottom-right, and bottom-left order
return np.array([tl, tr, br, bl], dtype="int32")
def perspective_transform(image, corners):
def order_corner_points(corners):
# Separate corners into individual points
# Index 0 - top-right
# 1 - top-left
# 2 - bottom-left
# 3 - bottom-right
corners = [(corner[0][0], corner[0][1]) for corner in corners]
top_r, top_l, bottom_l, bottom_r = corners[0], corners[1], corners[2], corners[3]
return (top_l, top_r, bottom_r, bottom_l)
# Order points in clockwise order
ordered_corners = order_corner_points(corners)
top_l, top_r, bottom_r, bottom_l = ordered_corners
# Determine width of new image which is the max distance between
# (bottom right and bottom left) or (top right and top left) x-coordinates
width_A = np.sqrt(((bottom_r[0] - bottom_l[0]) ** 2) + ((bottom_r[1] - bottom_l[1]) ** 2))
width_B = np.sqrt(((top_r[0] - top_l[0]) ** 2) + ((top_r[1] - top_l[1]) ** 2))
width = max(int(width_A), int(width_B))
# Determine height of new image which is the max distance between
# (top right and bottom right) or (top left and bottom left) y-coordinates
height_A = np.sqrt(((top_r[0] - bottom_r[0]) ** 2) + ((top_r[1] - bottom_r[1]) ** 2))
height_B = np.sqrt(((top_l[0] - bottom_l[0]) ** 2) + ((top_l[1] - bottom_l[1]) ** 2))
height = max(int(height_A), int(height_B))
# Construct new points to obtain top-down view of image in
# top_r, top_l, bottom_l, bottom_r order
dimensions = np.array([[0, 0], [width - 1, 0], [width - 1, height - 1],
[0, height - 1]], dtype = "float32")
# Convert to Numpy format
ordered_corners = np.array(ordered_corners, dtype="float32")
# Find perspective transform matrix
matrix = cv2.getPerspectiveTransform(ordered_corners, dimensions)
# Return the transformed image
return cv2.warpPerspective(image, matrix, (width, height))
image = cv2.imread('1.png')
original = image.copy()
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)
canny = cv2.Canny(gray, 120, 255, 1)
corners = cv2.goodFeaturesToTrack(canny,4,0.5,50)
c_list = []
for corner in corners:
x,y = corner.ravel()
c_list.append([int(x), int(y)])
cv2.circle(image,(x,y),5,(36,255,12),-1)
corner_points = np.array([c_list[0], c_list[1], c_list[2], c_list[3]])
ordered_corner_points = order_points_clockwise(corner_points)
mask = np.zeros(image.shape, dtype=np.uint8)
cv2.fillPoly(mask, [ordered_corner_points], (255,255,255))
mask = cv2.cvtColor(mask, cv2.COLOR_BGR2GRAY)
cnts = cv2.findContours(mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)
cnts = cnts[0] if len(cnts) == 2 else cnts[1]
for c in cnts:
peri = cv2.arcLength(c, True)
approx = cv2.approxPolyDP(c, 0.015 * peri, True)
if len(approx) == 4:
transformed = perspective_transform(original, approx)
result = rotate_image(transformed, -90)
cv2.imshow('canny', canny)
cv2.imshow('image', image)
cv2.imshow('mask', mask)
cv2.imshow('transformed', transformed)
cv2.imshow('result', result)
cv2.waitKey()
- найти контуры с опцией RETR_EXTERNAL.(серый -> фильтр Гаусса -> аккуратный край -> найти контур)
- найти контур наибольшего размера -> это будет край прямоугольника
находить углы с небольшим расчетом
Mat m;//image file findContours(m, contours_, hierachy_, RETR_EXTERNAL); auto it = max_element(contours_.begin(), contours_.end(), [](const vector<Point> &a, const vector<Point> &b) { return a.size() < b.size(); }); Point2f xy[4] = {{9000,9000}, {0, 1000}, {1000, 0}, {0,0}}; for(auto &[x, y] : *it) { if(x + y < xy[0].x + xy[0].y) xy[0] = {x, y}; if(x - y > xy[1].x - xy[1].y) xy[1] = {x, y}; if(y - x > xy[2].y - xy[2].x) xy[2] = {x, y}; if(x + y > xy[3].x + xy[3].y) xy[3] = {x, y}; }
xy[4] будет четырьмя углами. Таким образом я смог извлечь четыре угла.
Примените грубые линии к хитрому изображению - вы получите список точек, примените выпуклую оболочку к этому набору точек