Поиск подграфа в графике

Question

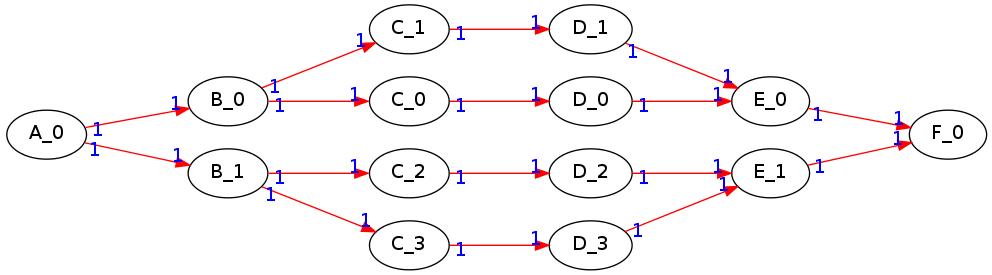
У меня есть график, показанный здесь. Просто узлу, что узлы B_0, B_1 принадлежат узлу типа B, C_0, C_1. C_2, C_3 принадлежат узлу типа C и так далее. Теперь я хочу найти несколько подграфов, которые могли бы удовлетворить критерии, определенные в этом примере:

Критерии -

1. подграф содержит 1 узел типа A, 1 узел типа B, 1 узел типа C, один узел типа D.
2. у подграфа есть одно ребро от узла типа A до одного узла типа B, одно ребро, соединяющее тип B и тип C, и одно ребро, соединяющее тип C и тип D.
3. подграф содержит одно ребро из типа A, выходящее из подграфа в узел типа B, одно ребро из типа B в узел типа C снаружи, одно ребро из типа D в тип E снаружи.

Теперь это описание должно дать результат как -

1. подграф:: A_0, B_0, C_1, D_1
2. подграф:: A_0, B_0, C_0, D_0
3. подграф:: A_0, B_1, C_2, D_2
4. подграф:: A_0, B_1, C_3, D_3

Я хочу знать, есть ли какой-нибудь алгоритм, по которому я могу найти такие подграфы? Я попытался выяснить алгоритм, составив все возможные комбинации. Однако это будет экспоненциально к числу узлов в подграфе. Таким образом, я хочу знать, существует ли эффективный способ его расчета. Или если в теории графов существует проблема аналогичного характера?

Answer 1

Вы можете начать с посещения всех узлов типа A. Для каждого узла A посмотрите все подключенные к нему узлы типа B. Оттуда посмотрите все узлы типа C и так далее, отслеживая посещенные вами узлы. от последнего узла. Затем, когда вы достигаете подузла, который удовлетворяет критериям вашего поиска, вы добавляете весь список узлов от узла A до точки, где вы находитесь. По сути, вы выполняете поиск в глубину, где вы продолжаете проходить по графику до тех пор, пока узел соответствует критериям того, что должно следовать, и возвращаться назад, когда больше нет действительных узлов (т. Е. Которые могли бы создать действительный подграф), выходящих из ваш текущий узел.