Как получить основную частоту, используя Harmonic Product Spectrum?

Question

Я пытаюсь получить высоту звука от входа микрофона. Сначала я разложил сигнал из временной области в частотную область через БПФ. Я применил окно Хемминга к сигналу перед выполнением БПФ. Тогда я получаю сложные результаты БПФ. Затем я передал результаты в спектр продуктов Harmonic, где результаты были подвергнуты понижающей дискретизации, а затем умножили пики пониженной дискретизации и дали значение в виде комплексного числа. Тогда что мне делать, чтобы получить основную частоту?

    public float[] HarmonicProductSpectrum(Complex[] data)
    {
        Complex[] hps2 = Downsample(data, 2);
        Complex[] hps3 = Downsample(data, 3);
        Complex[] hps4 = Downsample(data, 4);
        Complex[] hps5 = Downsample(data, 5);
        float[] array = new float[hps5.Length];

        for (int i = 0; i < array.Length; i++)
        {
            checked
            {
                array[i] = data[i].X * hps2[i].X * hps3[i].X * hps4[i].X * hps5[i].X;
            }
        }
        return array;
    }

    public Complex[] Downsample(Complex[] data, int n)
    {
        Complex[] array = new Complex[Convert.ToInt32(Math.Ceiling(data.Length * 1.0 / n))];
        for (int i = 0; i < array.Length; i++)
        {
            array[i].X = data[i * n].X;
        }
        return array;
    } 

Я пытался получить величину, используя,

    magnitude[i] = (float)Math.Sqrt(array[i] * array[i] + (data[i].Y * data[i].Y));  

внутри цикла for в методе HarmonicProductSpectrum. Затем попытался получить максимальный размер бина,

        float max_mag = float.MinValue;
        float max_index = -1;

        for (int i = 0; i < array.Length / 2; i++)
            if (magnitude[i] > max_mag)
            {
                max_mag = magnitude[i];
                max_index = i;
            }

а потом я попытался получить частоту, используя,

    var frequency = max_index * 44100 / 1024;

Но я получал значения мусора, такие как 1248,926, 1205,859, 2454,785 для ноты A4 (440 Гц), и эти значения не похожи на гармоники A4.

Помощь будет принята с благодарностью.

Answer 1

Я реализовал гармонический спектр продуктов в Python, чтобы убедиться, что ваши данные и алгоритм работают хорошо.

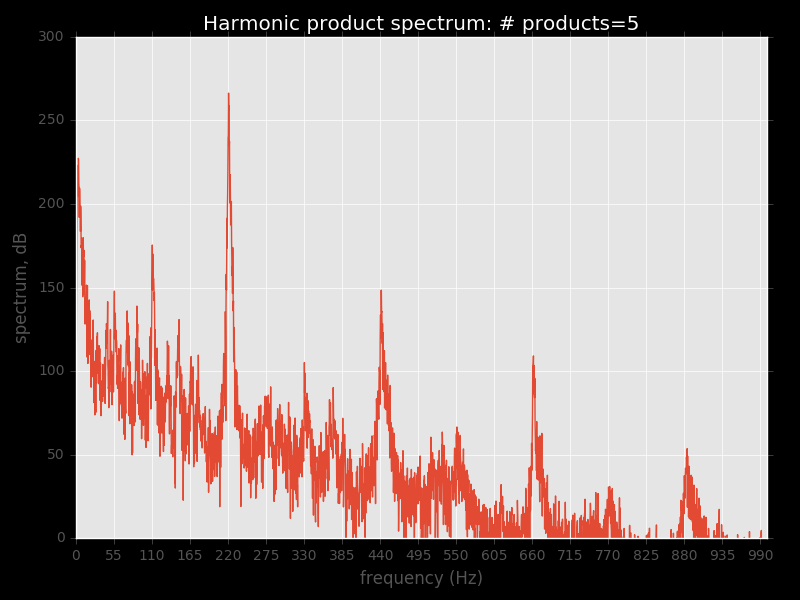
Вот что я вижу, применяя спектр гармонических произведений к полному набору данных с окном Хэмминга, с 5 этапами даун-сэмпла-умножения:

Это только нижний килогерц, но спектр в значительной степени мертв выше 1 кГц.

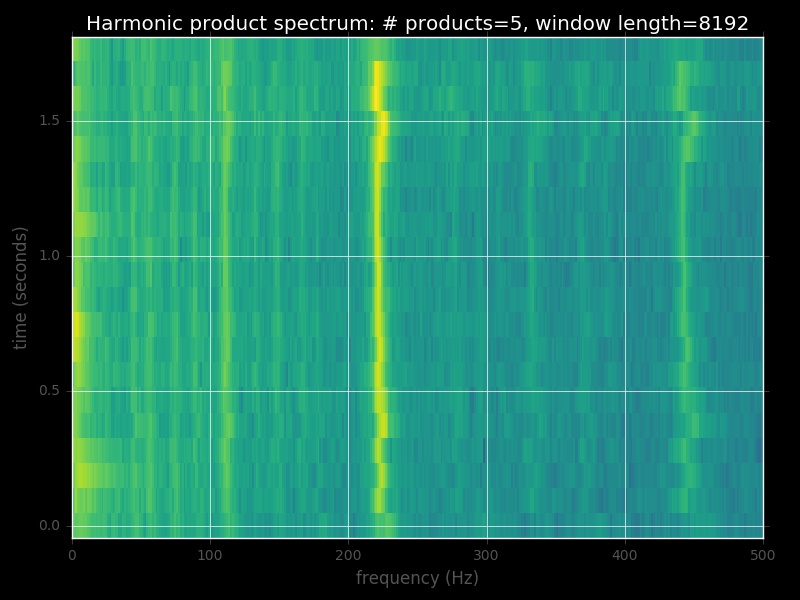
Если я разделю длинный аудиоклип на фрагменты с 8192 выборками (с перекрытием 5096 выборок на 50%) и окном Хемминга на каждый фрагмент и запуском HPS на нем, это матрица HPS. Это своего рода фильм спектра HPS по всему набору данных. Основная частота кажется достаточно стабильной.

Полный исходный код здесь- есть много кода, который помогает разбивать данные на части и визуализировать вывод HPS, работающего на чанках, но основная функция HPS, начиная с def hps(…, короткий. Но в нем есть несколько хитростей.

Учитывая странные частоты, на которых вы находите пик, возможно, вы работаете на полном спектре, от 0 до 44,1 кГц? Вы хотите сохранить только "положительные" частоты, т. Е. От 0 до 22,05 кГц, и применить алгоритм HPS (понижающая дискретизация – умножение).

Но если исходить из того, что вы используете спектр только с положительной частотой, правильно оцените его величину, похоже, вы должны получить разумные результаты. Попробуйте сохранить выход вашего HarmonicProductSpectrum чтобы увидеть, если это что-то вроде выше.

Опять же, полный исходный код находится по адресу https://gist.github.com/fasiha/957035272009eb1c9eb370936a6af2eb. (Там я опробую другую пару спектральных оценок, метод Уэлча от Scipy и мой порт спектральной оценки Блэкмена-Тьюки. Я не уверен, настроены ли вы на реализацию HPS или вы рассматриваете другие оценки основного тона, поэтому я ' я оставляю там результаты Уэлча / Блэкмена-Тьюки.)

---

Оригинал Я написал это как комментарий, но должен был продолжать его пересматривать, потому что это сбивало с толку, так что вот как мини-ответ.

Основываясь на кратком прочтении этого вступления к HPS, я не думаю, что вы правильно оценили величины после того, как нашли четыре прореженных ответа.

Ты хочешь:

array[i] = sqrt(data[i] * Complex.conjugate(data[i]) *
                hps2[i] * Complex.conjugate(hps2[i]) *
                hps3[i] * Complex.conjugate(hps3[i]) *
                hps4[i] * Complex.conjugate(hps4[i]) *
                hps5[i] * Complex.conjugate(hps5[i])).X;

Это использует sqrt(x * Complex.conjugate(x)) хитрость, чтобы найти xВеличина, а затем умножает все 5 величин.

(На самом деле, это перемещает sqrt вне продукта, так что вы делаете только один sqrt, экономит время, но дает тот же результат. Так что, может быть, это еще один трюк.)

Последний трюк: он принимает реальную роль этого результата, потому что иногда из-за проблем с плавающей точкой крошечный мнимый компонент, такой как 1e-15, выживает.

После того, как вы это сделаете, array должен содержать только реальный floatс, и вы можете применить поиск максимального бен.

---

Если нет Conjugate Метод, то по старинке должен работать:

public float mag2(Complex c) { return c.X * c.X + c.Y * c.Y; }

// in HarmonicProductSpectrum 
array[i] = sqrt(mag2(data[i]) * mag2(hps2[i]) * mag2(hps3[i]) * mag2(hps4[i]) * mag2(hps5[i]));

Есть алгебраические недостатки с двумя подходами, которые вы предложили в комментариях ниже, но вышеупомянутое должно быть правильным. Я не уверен, что делает C#, когда вы назначаете Complex для float - может быть, он использует реальный компонент? Я бы подумал, что это будет ошибка компилятора, но с приведенным выше кодом, вы делаете правильные вещи со сложными данными, и только назначая float в array[i],

Answer 2

Чтобы получить оценку основного тона, вы должны разделить оценку частоты суммированного бина на коэффициент понижающей дискретизации, используемый для этой суммы.

Добавлено: Вы также должны суммировать величины (abs()), а не принимать величину комплексной суммы.

Но алгоритм спектра гармонических произведений (HPS), особенно при использовании только целочисленных коэффициентов понижающей дискретизации, обычно не обеспечивает лучшего разрешения оценки основного тона. Вместо этого он обеспечивает более надежную грубую оценку основного тона (с меньшей вероятностью, которая будет одурачена гармоникой), чем использование одиночного пика абсолютной величины FFT для последовательных богатых обертонов тембров, которые имеют слабое или пропускающее основное спектральное содержание.

Если вы знаете, как уменьшить частоту спектра с помощью дробных соотношений (используя интерполяцию и т. Д.), Вы можете попробовать более точную понижающую дискретизацию, чтобы получить лучшую оценку основного тона из HPS. Или вы можете использовать результат HPS, чтобы проинформировать вас о более узком диапазоне частот, в котором нужно искать, используя другой метод оценки основного тона или частоты.