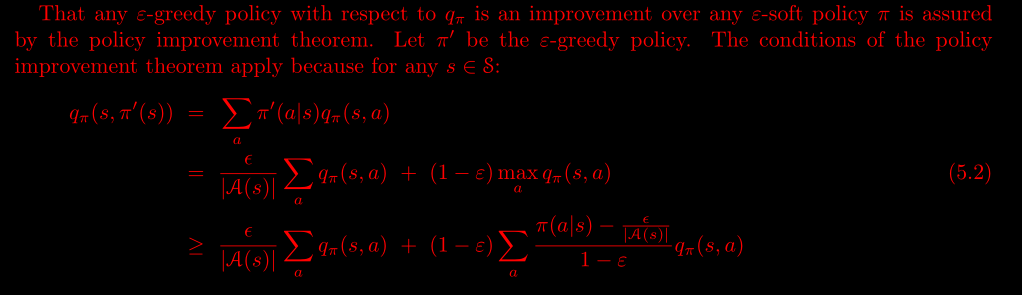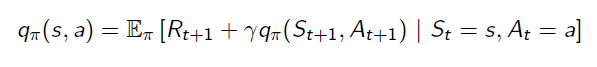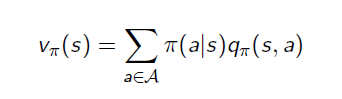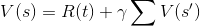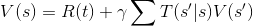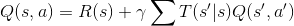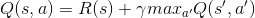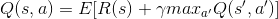Путаница в понимании формулы Q(s,a) для обучения усилению MDP?

Question

Я пытался понять, почему теорема улучшения политики может быть применена к эпсилон-жадной политике.

Доказательство начинается с математического определения -

Я запутался в самой первой строке доказательства.

Это уравнение является уравнением ожидания Беллмана для Q(s,a), тогда как V(s) и Q (s, a) следуют соотношению -

Так как же мы можем получить первую строку доказательства?

Answer 1

Задача оптимального управления была впервые введена в 1950-х годах. Проблема заключалась в том, чтобы разработать контроллер для максимизации или минимизации целевой функции. Ричард Беллман подошел к этой задаче оптимального управления, введя уравнение Беллмана:

Где значение эквивалентно дисконтированной сумме вознаграждений. Если мы сделаем первый шаг, мы получим следующее:

Впоследствии классическое обучение с подкреплением основано на процессе принятия решений Маркова и предполагает, что все переходы между состояниями известны. Таким образом, уравнение становится следующим:

То есть суммирование эквивалентно суммированию всех возможных переходов из этого состояния, умноженному на вознаграждение за достижение нового состояния.

Вышеуказанные уравнения записаны в виде значения. Иногда мы хотим, чтобы значение также было функцией действия, создавая, таким образом, значение действия. Преобразование вышеприведенного уравнения в форму значения действия:

Самая большая проблема с этим уравнением состоит в том, что в реальной жизни переходные вероятности фактически не известны. Невозможно узнать переходные вероятности каждого отдельного состояния, если проблема не предельно проста. Чтобы решить эту проблему, мы обычно просто берем максимум будущей дисконтированной части. То есть мы предполагаем, что в будущем мы будем вести себя оптимально, а не усреднять все возможные сценарии.

Однако в реальном сценарии среда может быть сильно стохастической. Следовательно, лучшая оценка функции-значения в любом состоянии - это просто оценка. И пост вероятностный случай - ожидаемое значение. Таким образом, давая вам:

Обозначение награды - это t+1 в вашем уравнении. Это в основном из-за разных интерпретаций. Приведенное выше доказательство остается верным для вашей записи. Это просто говорит, что вы не будете знать свою награду, пока не дойдете до следующего времени отбора проб.