Как использовать Mathematica для решения численного дифференцирования и интеграции в моем коде?

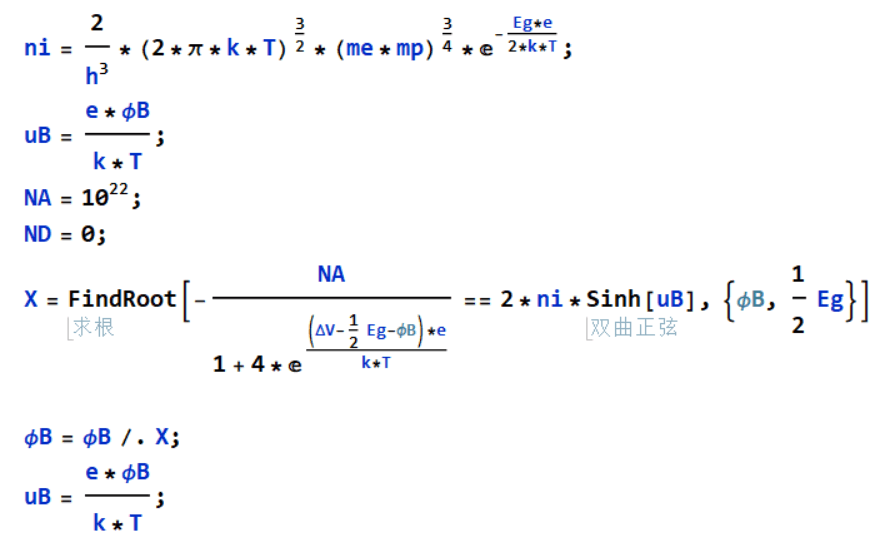
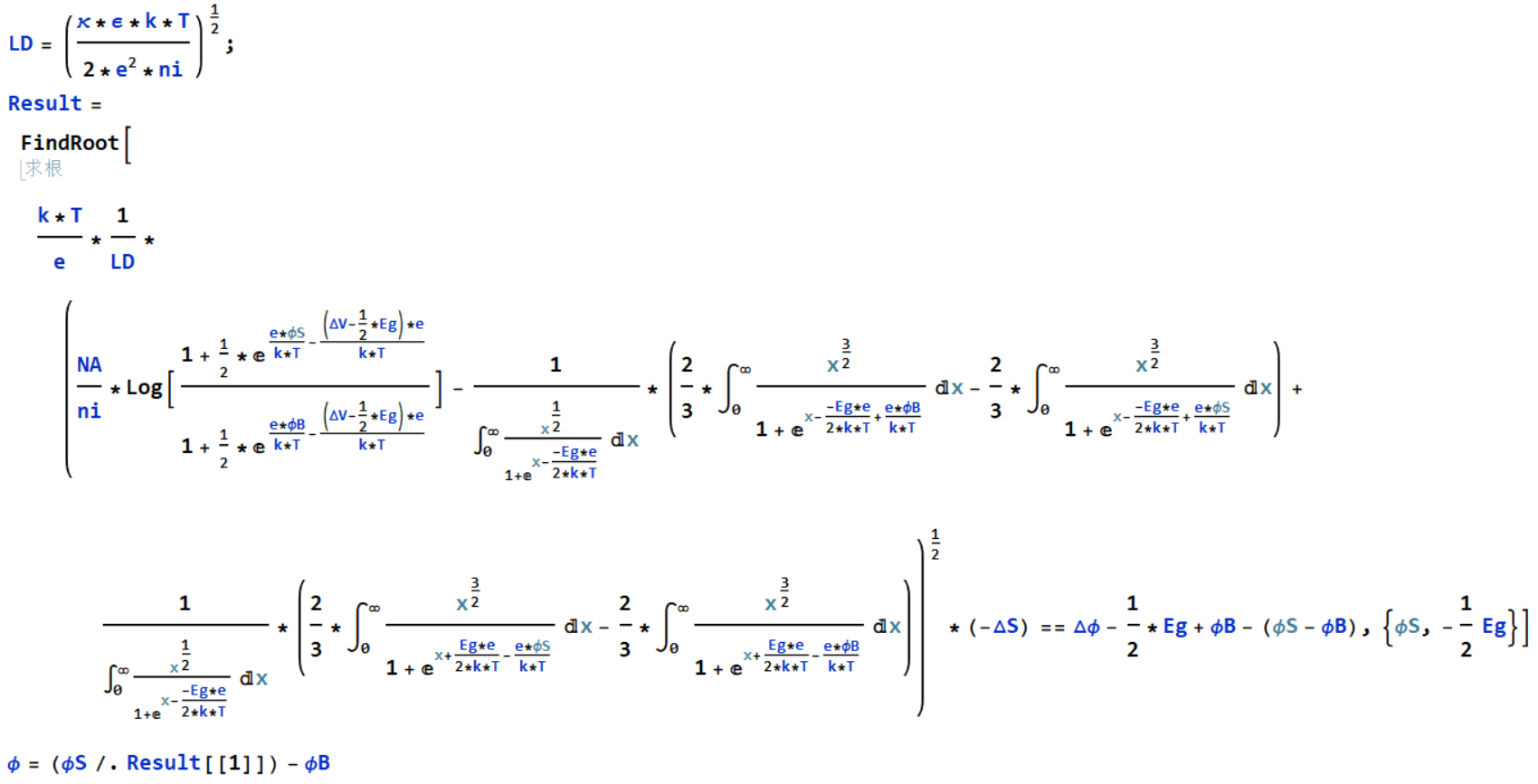

Я использую параметры для расчета Φ в финале, но я не знаю, что произойдет, это показывает много информации, но я не могу понять. Я использую этот код для решения проблемы. Этот код заимствован мной. С согласия других я ничего не изменил, но не могу показать окончательный результат. Основная проблема в последнем расчете FindRoot, Следуйте мой код.
Надеюсь, кто-нибудь может мне помочь, большое спасибо! Потому что эта проблема очень важна для меня!
(* Physical Constants *)
k = 1.38 * 10^-23;
ϵ = 8.85 * 10^-12;
e = 1.6 *10^-19;
m0 = 9.11 * 10^-31;
h = 6.63 * 10^-34;
(* Basic information of Black Phosphorus *)
κ = 6.1;
me = 0.13 * m0;
mp = 0.28 * m0;
Eg = 0.33;
Δϕ = -0.1;
(* Δϕ = ϕTip - χ *)
ΔV = 0.04;
(* ΔV = EA - EV *)
(* Experimental conditions *)
T = 4.3;
ΔS = 0.4*10^-9;
(* Distance between tip and sample *)
ni = 2/h^3*(2*π*k*T)^(3/2)*(me*mp)^(3/4)*E^(-((Eg*e)/(2*k*T)));
uB = (e*ϕB)/(k*T);
NA = 10^22;
ND = 0;
X = FindRoot[-(NA/(
1 + 4*E^(((ΔV - 1/2 Eg - ϕB)*e)/(k*T)))) ==
2*ni*Sinh[uB], {ϕB, 1/2 Eg}]
ϕB = ϕB /. X;
uB = (e*ϕB)/(k*T);
LD = ((κ*ϵ*k*T)/(2*e^2*ni))^(1/2);
Result = FindRoot[(k*T)/e*1/
LD*(NA/ni*
Log[(1 +
1/2*E^((e*ϕS)/(k*T) - ((ΔV - 1/2*Eg)*e)/(
k*T)))/(
1 + 1/2*E^((e*ϕB)/(
k*T) - ((ΔV - 1/2*Eg)*e)/(k*T)))] - 1/\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(1\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x -
\*FractionBox[\(\(-Eg\)*e\), \(2*k*
T\)]\)]\)] \[DifferentialD]x\)\)*(2/3*\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(3\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x -
\*FractionBox[\(\(-Eg\)*e\), \(2*k*T\)] +
\*FractionBox[\(e*ϕB\), \(k*T\)]\)]\)] \[DifferentialD]x\)\) -
2/3*\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(3\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x -
\*FractionBox[\(\(-Eg\)*e\), \(2*k*T\)] +
\*FractionBox[\(e*ϕS\), \(k*T\)]\)]\)] \[DifferentialD]x\)\)) +
1/\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(1\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x -
\*FractionBox[\(\(-Eg\)*e\), \(2*k*
T\)]\)]\)] \[DifferentialD]x\)\)*(2/3*\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(3\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x +
\*FractionBox[\(Eg*e\), \(2*k*T\)] -
\*FractionBox[\(e*ϕS\), \(k*T\)]\)]\)] \[DifferentialD]x\)\) -
2/3*\!\(
\*SubsuperscriptBox[\(∫\), \(0\), \(∞\)]\(
\*FractionBox[
SuperscriptBox[\(x\),
FractionBox[\(3\), \(2\)]], \(1 +
\*SuperscriptBox[\(E\), \(x +
\*FractionBox[\(Eg*e\), \(2*k*T\)] -
\*FractionBox[\(e*ϕB\), \(k*T\)]\)]\)] \[DifferentialD]x\)\)))^(
1/2)*(-ΔS) == Δϕ -
1/2*Eg + ϕB - (ϕS - ϕB), {ϕS, -(1/2) Eg}]
ϕ = (ϕS /. Result[[1]]) - ϕB
1 ответ
Попробуйте ВНИМАТЕЛЬНО скрести это в новую пустую записную книжку и оценить ее прежде всего.
(* Physical Constants *)
k = 1.38 * 10^-23;
ε = 8.85 * 10^-12;
e = 1.6 *10^-19;
m0 = 9.11 * 10^-31;
h = 6.63 * 10^-34;
(* Basic information of Black Phosphorus *)
κ = 6.1;
me = 0.13 * m0;
mp = 0.28 * m0;
Eg = 0.33;
Δφ = -0.1;
(* Δφ = φTip - χ *)
ΔV = 0.04;
(* ΔV = EA - EV *)
(* Experimental conditions *)
T = 4.3;
ΔS = 0.4*10^-9;
(* Distance between tip and sample *)
ni = 2/h^3*(2*Pi*k*T)^(3/2)*(me*mp)^(3/4)*E^(-((Eg*e)/(2*k*T)));
uB = (e*φB)/(k*T);
NA = 10^22;
ND = 0;
X = FindRoot[-(NA/(1+4*E^(((ΔV-1/2 Eg-φB)*e)/(k*T))))==2*ni*Sinh[uB], {φB, 1/2 Eg}];
φB = φB /. X;
uB = (e*φB)/(k*T);
LD = ((κ*ε*k*T)/(2*e^2*ni))^(1/2);
Result = FindRoot[(k*T)/e*1/LD*(NA/ni*
Log[(1 + 1/2*E^((e*φS)/(k*T) - ((ΔV - 1/2*Eg)*e)/(k*T)))/
(1 + 1/2*E^((e*φB)/(k*T) - ((ΔV - 1/2*Eg)*e)/(k*T)))] -
1/Integrate[x^(1/2)/(1+E^((e*Eg)/(2*k*T)+x)), {x, 0, Infinity}]*
(2/3*Integrate[x^(3/2)/(1+E^((e*Eg)/(2*k*T)+x+(e*φB)/(k*T))), {x, 0, Infinity}] -
2/3*Integrate[x^(3/2)/(1+E^((e*Eg)/(2*k*T)+x+(e*φS)/(k*T))), {x, 0, Infinity}]) +
1/Integrate[x^(1/2)/(1+E^((e*Eg)/(2*k*T)+x)), {x, 0, Infinity}]*
(2/3*Integrate[x^(3/2)/(1+E^((e*Eg)/(2*k*T)+x-(e*φS)/(k*T))), {x, 0, Infinity}] -
2/3*Integrate[x^(3/2)/(1+E^((e*Eg)/(2*k*T)+x-(e*φB)/(k*T))), {x, 0, Infinity}]))^(1/2)*
(-ΔS) == Δφ - 1/2*Eg + φB - (φS - φB), {φS, -(1/2) Eg}];
φ = (φS /. Result[[1]]) - φB
(*-0.324431*)