Нахождение бета-тета-обозначения функции

Question

Итак, у меня есть цикл, встроенный в цикл здесь:

int a,b,n;
for (a = 1; a <=n; a++) {
    for (b = 0; b < n; b+=a)
        cout << "hey" << endl;
}

n является степенью 2

Я пытаюсь понять, как рассчитать сложность Времени, но у меня возникли проблемы с определением для этого биг-тета-нотации.

Я знаю, что внешний цикл запускается за O(n), но я не уверен насчет внутреннего цикла из-за b+=a. Я знаю, что если бы у меня было время для обоих циклов, я мог бы умножить их, чтобы получить время Big-theta для функции, но я не уверен, на что работает внутренний цикл.

Когда я подключаю образцы n (т.е. 2, 4, 8, 16), то внутренний цикл повторяется 3, 9, 24, 61 раз соответственно. Я не вижу, как эти значения коррелируют.

Редактировать:

Хорошо, я понимаю, что вы говорите, но я пытаюсь сравнить это с этой функцией. Что будет время для этой функции? Тогда я могу сравнить скорость двух:

int a,b,n;
int z = 1;
for (a = 0; a <n; a++) {
    for (b = 0; b < n; b=b+z)
        cout << "hey" << endl;
    z = z * 2;
}

Answer 1

Вы можете видеть, что внутренний цикл выполняет количество включений a в n, то есть наибольшее целое число k, которое удовлетворяет:

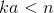
Это соответствует функции потолка. Итак, общее количество итераций внутреннего цикла:

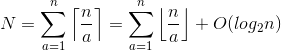
Вторая сумма - сумматорная функция делителя, которую можно записать так:

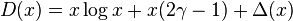
Таким образом, временная сложность всего кода равна O(nlogn).

РЕДАКТИРОВАТЬ

Что касается второго фрагмента кода, который вы разместили, расчеты проще. Если n=2^kколичество итераций:

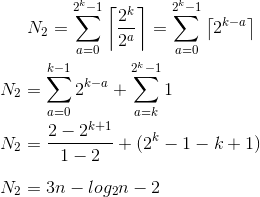
Так что второй быстрее, так как это O(n).