Интеграция орбит с гравитационными полями Солнечной системы от Skyfield - проблемы скорости
В тестах времени, показанных ниже, я обнаружил, что Skyfield требуется несколько сотен микросекунд до миллисекунды, чтобы вернуться obj.at(jd).position.km для одного значения времени в jd, но дополнительные затраты дольше JulianDate Объекты (список точек во времени) составляют всего около одной микросекунды на точку. Я вижу похожие скорости, используя Jplephem и с двумя разными эфемеридами.
Мой вопрос здесь таков: если я хочу использовать точки произвольного доступа во времени, например, в качестве раба для внешней подпрограммы Рунге-Кутты, которая использует собственный переменный размер шага, есть ли способ сделать это быстрее в Python (без необходимости научиться компилировать код)?
Я понимаю, что это совсем не типичный способ использования Skyfield. Обычно мы загружаем JulianDate объект с длинным списком временных точек, а затем рассчитать их сразу, и, вероятно, сделать это несколько раз, а не тысячи раз (или больше), как это может сделать интегратор орбиты.
Обходной путь: я могу вообразить обходной путь, где я строю свой собственный NumPy базы данных, запустив Skyfield один раз, используя JulianDate объект с высокой степенью детализации по времени, затем пишу собственную подпрограмму Рунге-Кутты, которая изменяет размеры шага вверх и вниз на дискретные величины, так что временные шаги всегда соответствуют шагу массива NumPy.
Или я мог бы даже попытаться повторить интерполяцию. Я не делаю очень точных вычислений, поэтому может подойти простой порядок NumPy или SciPy 2-го порядка.
В конечном итоге я хотел бы попытаться интегрировать траекторию объектов под воздействием гравитационного поля Солнечной системы (например, спутник в дальнем космосе, комета, астероид). При поиске решения орбиты можно попробовать миллионы векторов начального состояния в 6D фазовом пространстве. Я знаю, что я должен использовать такие вещи, как ob.at(jd).observe(large_body).position.km метод, потому что гравитация движется со скоростью света, как и все остальное. Похоже, это стоит значительного времени, поскольку (я предполагаю) это итеративный расчет ("Давайте посмотрим... где бы Юпитер был таким, чтобы я чувствовал, что это гравитация прямо сейчас"). Но давайте очистим космический лук по одному слою за раз.
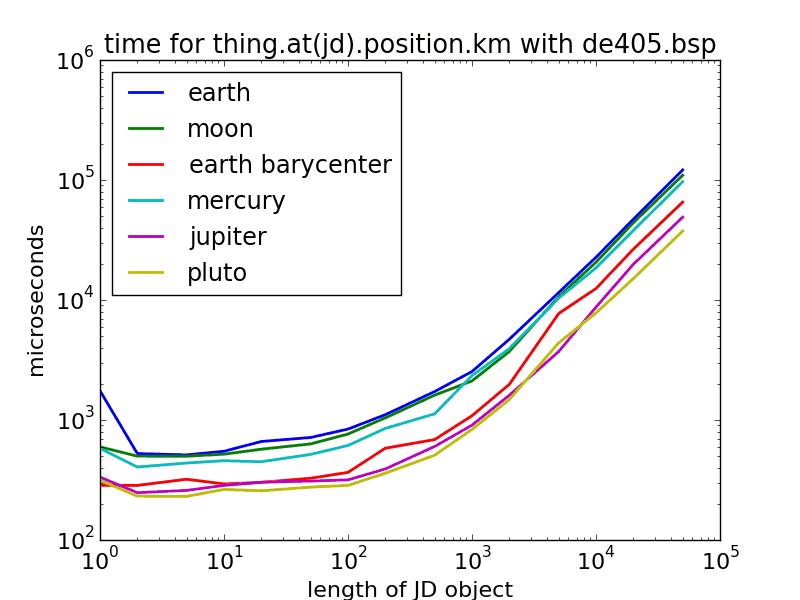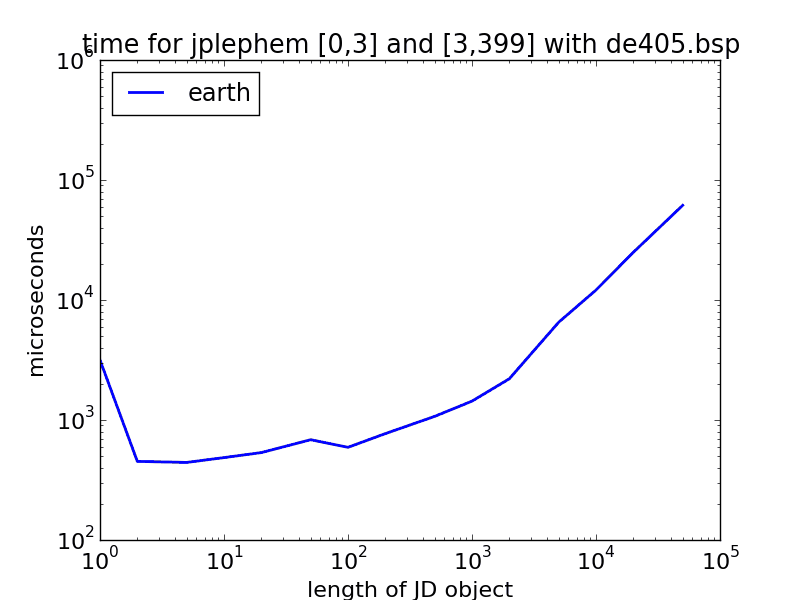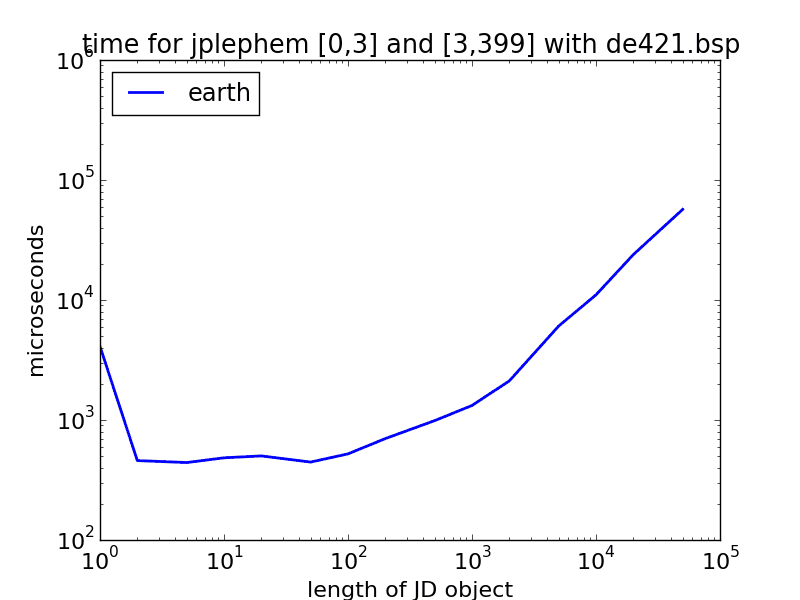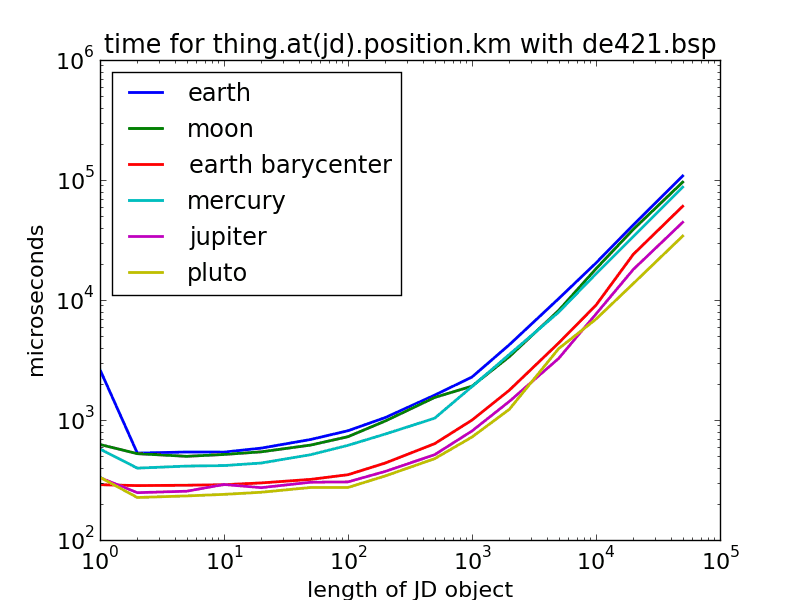
Рисунок 1. Производительность Skyfield и JPLephem на моем ноутбуке для различной длины JulianDate объекты, для de405 и de421. Все они примерно одинаковы - (очень) примерно полмиллисекунды для первой точки и микросекунды для каждой дополнительной точки. Также самая первая точка, которая будет рассчитана при запуске сценария (Земля (синяя) с len(jd) = 1) имеет дополнительный миллисекундный артефакт.
Земля и Луна медленнее, потому что это двухшаговое вычисление внутри (Барицентр Земля-Луна плюс отдельные орбиты вокруг Барицентра). Ртуть может быть медленнее, потому что она движется так быстро по сравнению с временными шагами эфемерид, что требует больше коэффициентов в (дорогостоящей) чебышевской интерполяции?
СЦЕНАРИЙ ДЛЯ НЕБОЛЬШИХ ДАННЫХ, сценарий JPLephem находится ниже
import numpy as np
import matplotlib.pyplot as plt
from skyfield.api import load, JulianDate
import time
ephem = 'de421.bsp'
ephem = 'de405.bsp'
de = load(ephem)
earth = de['earth']
moon = de['moon']
earth_barycenter = de['earth barycenter']
mercury = de['mercury']
jupiter = de['jupiter barycenter']
pluto = de['pluto barycenter']
things = [ earth, moon, earth_barycenter, mercury, jupiter, pluto ]
names = ['earth', 'moon', 'earth barycenter', 'mercury', 'jupiter', 'pluto']
ntimes = [i*10**n for n in range(5) for i in [1, 2, 5]]
years = [np.zeros(1)] + [np.linspace(0, 100, n) for n in ntimes[1:]] # 100 years
microsecs = []
for y in years:
jd = JulianDate(utc=(1900 + y, 1, 1))
mics = []
for thing in things:
tstart = time.clock()
answer = thing.at(jd).position.km
mics.append(1E+06 * (time.clock() - tstart))
microsecs.append(mics)
microsecs = np.array(microsecs).T
many = [len(y) for y in years]
fig = plt.figure()
ax = plt.subplot(111, xlabel='length of JD object',
ylabel='microseconds',
title='time for thing.at(jd).position.km with ' + ephem )
for item in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(item.get_fontsize() + 4) # http://stackru.com/a/14971193/3904031
for name, mics in zip(names, microsecs):
ax.plot(many, mics, lw=2, label=name)
plt.legend(loc='upper left', shadow=False, fontsize='x-large')
plt.xscale('log')
plt.yscale('log')
plt.savefig("skyfield speed test " + ephem.split('.')[0])
plt.show()
СЦЕНАРИЙ ДЛЯ JPLEPHEM ДАННЫХ сценарий Skyfield выше
import numpy as np
import matplotlib.pyplot as plt
from jplephem.spk import SPK
import time
ephem = 'de421.bsp'
ephem = 'de405.bsp'
kernel = SPK.open(ephem)
jd_1900_01_01 = 2415020.5004882407
ntimes = [i*10**n for n in range(5) for i in [1, 2, 5]]
years = [np.zeros(1)] + [np.linspace(0, 100, n) for n in ntimes[1:]] # 100 years
barytup = (0, 3)
earthtup = (3, 399)
# moontup = (3, 301)
microsecs = []
for y in years:
mics = []
#for thing in things:
jd = jd_1900_01_01 + y * 365.25 # roughly, it doesn't matter here
tstart = time.clock()
answer = kernel[earthtup].compute(jd) + kernel[barytup].compute(jd)
mics.append(1E+06 * (time.clock() - tstart))
microsecs.append(mics)
microsecs = np.array(microsecs)
many = [len(y) for y in years]
fig = plt.figure()
ax = plt.subplot(111, xlabel='length of JD object',
ylabel='microseconds',
title='time for jplephem [0,3] and [3,399] with ' + ephem )
# from here: http://stackru.com/a/14971193/3904031
for item in ([ax.title, ax.xaxis.label, ax.yaxis.label] +
ax.get_xticklabels() + ax.get_yticklabels()):
item.set_fontsize(item.get_fontsize() + 4)
#for name, mics in zip(names, microsecs):
ax.plot(many, microsecs, lw=2, label='earth')
plt.legend(loc='upper left', shadow=False, fontsize='x-large')
plt.xscale('log')
plt.yscale('log')
plt.ylim(1E+02, 1E+06)
plt.savefig("jplephem speed test " + ephem.split('.')[0])
plt.show()