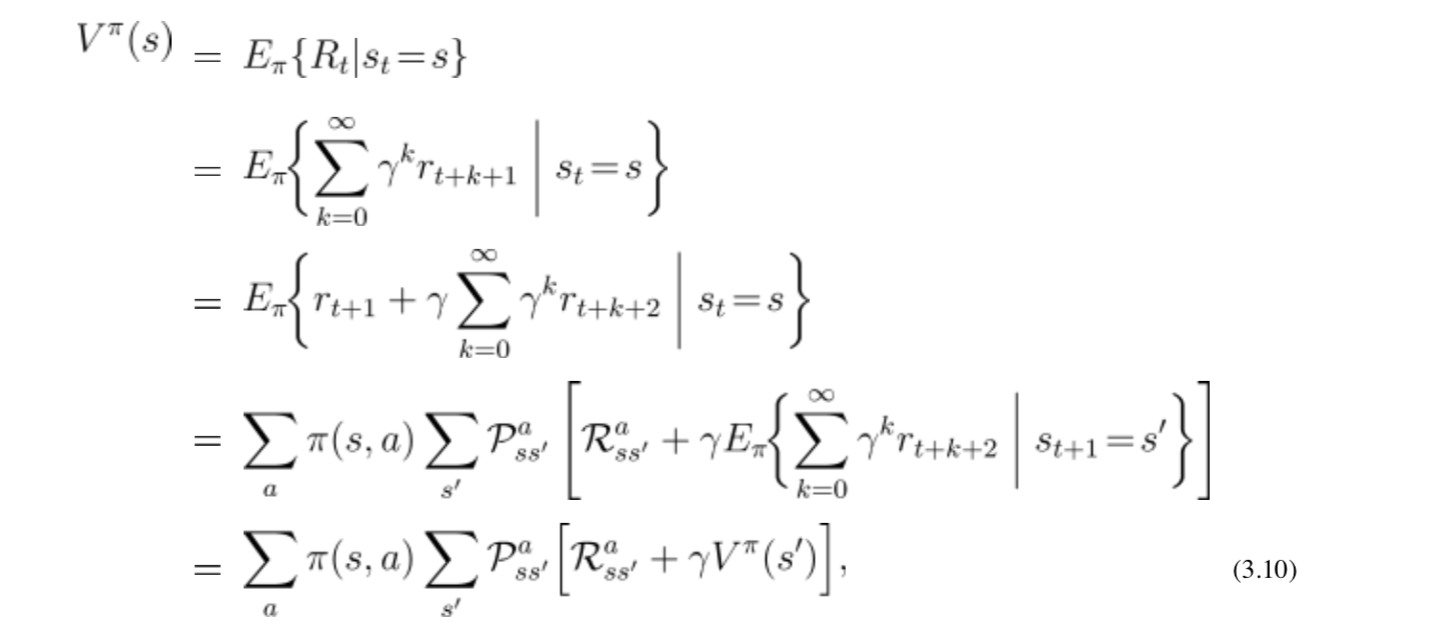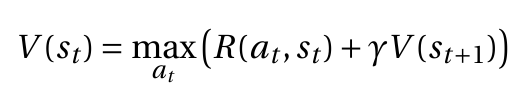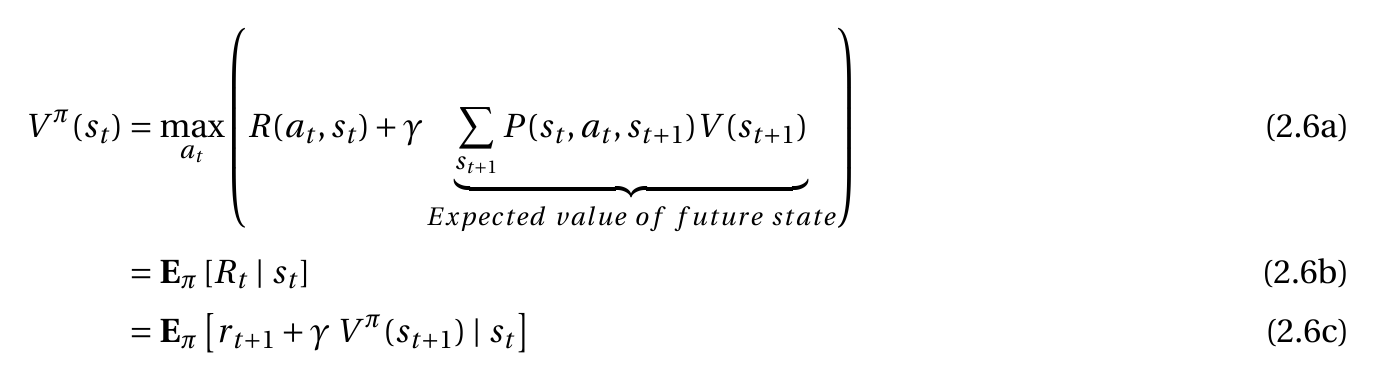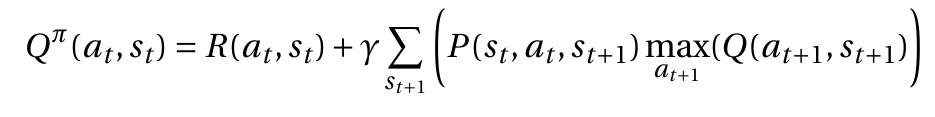Государственное значение и государственные ценности действия с политикой - уравнение Беллмана с политикой
Я только начинаю с глубокого обучения подкреплению, и я пытаюсь разрушить эту концепцию.
У меня есть это детерминированное уравнение Беллмана
Когда я реализую Stochastacity из MDP, я получаю 2.6a
Мое уравнение это предположение правильно. Я видел эту реализацию 2.6a без знака политики для функции значения состояния. Но для меня это не имеет смысла, потому что я использую вероятность того, на каких разных следующих шагах я мог бы закончить. Я думаю, это то же самое, что сказать "политика". и если да, 2.6a является правильным, могу ли я тогда предположить, что остальные (2.6b и 2.6c), потому что тогда я хотел бы написать функцию состояния действия следующим образом:
Причина, по которой я так поступаю, заключается в том, что я хотел бы объяснить себя с детерминированной точки зрения на недетерминированную точку зрения.
Я надеюсь, что кто-то может помочь в этом!
С наилучшими пожеланиями Сорен Кох
2 ответа
Нет, функция значения V(s_t) не зависит от политики. Вы видите в уравнении, что оно определяется с точки зрения действия a_t это максимизирует количество, поэтому оно не определяется с точки зрения действий, выбранных какой-либо политикой.
В недетерминированном / стохастическом случае эта сумма будет превышать вероятности, умноженные на значения состояния, но она все еще не зависит от какой-либо политики. Сумма суммируется только по различным возможным будущим состояниям, но каждое умножение включает в себя одно и то же (независимое от политики) действие a_t, Единственная причина, по которой у вас есть эти вероятности, заключается в том, что в недетерминированном случае конкретное действие в определенном состоянии может привести к одному из нескольких возможных состояний. Это происходит не из-за политики, а из-за стохастичности самой среды.
Также существует такая вещь, как функция значения для политик, и когда речь идет об этом, необходимо включить символ для политики. Но обычно это не то, что подразумевается под "функцией значения", а также не соответствует уравнению, которое вы нам показали. Функция, зависящая от политики, заменит max_{a_t} с суммой по всем действиям aи внутри суммы вероятность pi(s_t, a) политики pi выбирая действие a в состоянии s_t,
Да, ваше предположение совершенно верно. В поле "Обучение усилению" функция значения - это результат, полученный путем запуска для определенного состояния и следования политике π . Так что да, строго говоря, это должно сопровождаться политическим знаком π .
Уравнение Беллмана в основном представляет функции значения рекурсивно. Однако следует отметить, что существует два вида уравнений Беллмана:
Уравнение оптимальности Беллмана, характеризующее функции оптимального значения. В этом случае значение функции у него неявно связано с оптимальной политикой. Это уравнение имеет нелинейный
maxоператор и тот, который вы опубликовали. (Оптимальная) зависимость от политики иногда обозначается звездочкой следующим образом: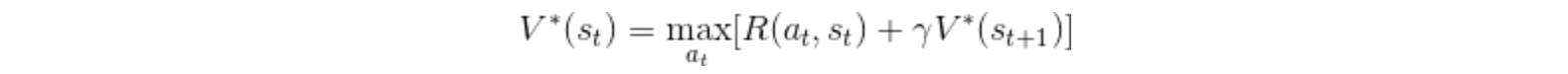
Возможно, некоторые короткие тексты или статьи опускают эту зависимость, предполагая, что она очевидна, но я думаю, что любой учебник по RL должен изначально включать ее. См., Например, Sutton & Barto или Busoniu et al. книг.Уравнение Беллмана, которое характеризует функцию значения, в этом случае связано с любой политикой π:
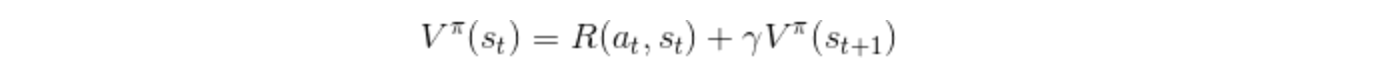
В вашем случае ваше уравнение 2.6 основано на уравнении Беллмана, поэтому оно должно удалить max оператор и включить сумму по всем действиям и возможным следующим состояниям. От Sutton & Barto (извините за изменение обозначений относительно вашего вопроса, но я думаю, что он нестабилен): 