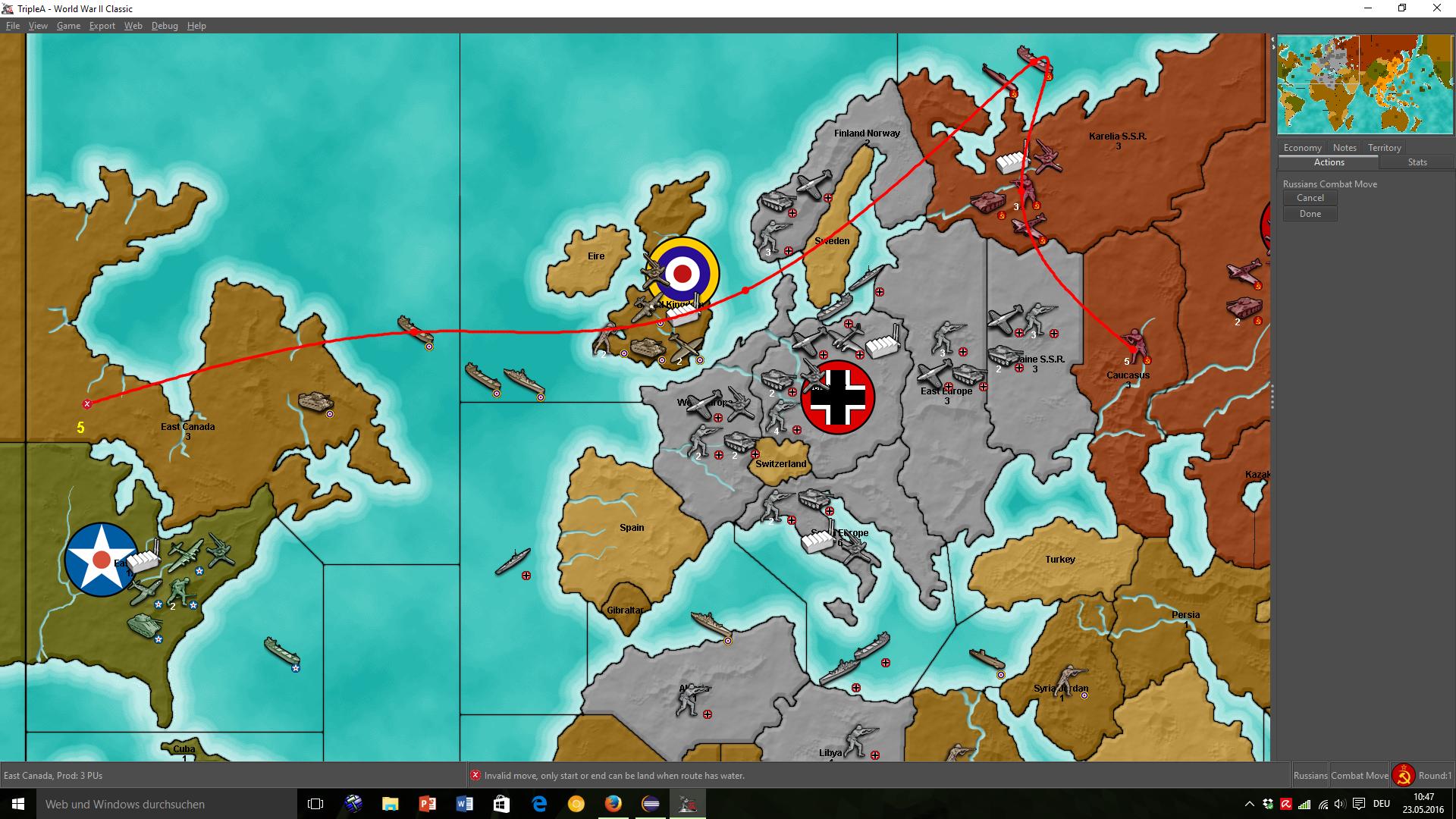
Как правильно нарисовать путь?

Question

В настоящее время я работаю над переписыванием алгоритма рисования контура. Я использую сплайн-интерполятор apache-commons-math для получения плавного пути через все заданные точки в 2D-пространстве...

В настоящее время у меня есть:

/**
 * Draws a route on a map.
 */
public class MapRouteDrawer {

  private static final SplineInterpolator splineInterpolator = new SplineInterpolator();

  /**
   * Draws the route to the screen, does nothing if null.
   */
  public static void drawRoute(final Graphics2D graphics, final RouteDescription routeDescription, final MapPanel view, final MapData mapData, final String movementLeftForCurrentUnits) {
    if (routeDescription == null) {
      return;
    }
    final Route route = routeDescription.getRoute();
    if (route == null) {
      return;
    }

    final Point[] points = getRoutePoints(routeDescription, mapData);
    final int xOffset = view.getXOffset();
    final int yOffset = view.getYOffset();
    final int jointsize = 10;
    final int numTerritories = route.getAllTerritories().size();
    //set thickness and color of the future drawings
    graphics.setStroke(new BasicStroke(3.5f, BasicStroke.CAP_ROUND, BasicStroke.JOIN_ROUND));
    graphics.setPaint(Color.red);
    graphics.setRenderingHint(RenderingHints.KEY_ANTIALIASING, RenderingHints.VALUE_ANTIALIAS_ON);

    if(Arrays.asList(points).contains(null)){//If the Array is null at some point
      return;
    }

    if(numTerritories <= 1 || points.length <= 2){
      drawLineWithTranslate(graphics, new Line2D.Float(routeDescription.getStart(), routeDescription.getEnd()), xOffset, yOffset);
      graphics.fillOval((routeDescription.getEnd().x - xOffset) - jointsize / 2, (routeDescription.getEnd().y - yOffset) - jointsize / 2, jointsize, jointsize);
    }
    else{
      drawCurvedPath(graphics, points, view);
    }
  }

  }

  private static double[] getIndex(Point[] points) {
    final double[] index = new double[points.length];
    for(int i = 0; i < points.length; i++){
      index[i] = i;
    }
    return index;
  }

  private static void drawLineWithTranslate(Graphics2D graphics, Line2D line2D, double translateX, double translateY) {
      final Line2D line = (Line2D) line2D;
      final Point2D point1 = new Point2D.Double(line.getP1().getX() - translateX, line.getP1().getY() - translateY);
      final Point2D point2 = new Point2D.Double(line.getP2().getX() - translateX, line.getP2().getY() - translateY);
      graphics.draw(new Line2D.Double(point1, point2));
  }

  private static Point[] getRoutePoints(RouteDescription routeDescription, MapData mapData){
    final List<Territory> territories = routeDescription.getRoute().getAllTerritories();
    final int numTerritories = territories.size();
    final Point[] points = new Point[numTerritories];
    for (int i = 0; i < numTerritories; i++) {
      points[i] = mapData.getCenter(territories.get(i));
    }
    if (routeDescription.getStart() != null) {
      points[0] = routeDescription.getStart();
    }
    if (routeDescription.getEnd() != null && numTerritories > 1) {
      points[numTerritories - 1] = new Point(routeDescription.getEnd());
    }
    return points;
  }

  private static double[] pointsXToDoubleArray(Point[] points){
    double[] result = new double[points.length];
    for(int i = 0; i < points.length; i++){
      result[i] = points[i].getX();
    }
    return result;
  }
  private static double[] pointsYToDoubleArray(Point[] points){
    double[] result = new double[points.length];
    for(int i = 0; i < points.length; i++){
      result[i] = points[i].getY();
    }
    return result;
  }

  private static double[] getCoords(PolynomialSplineFunction curve, float stepSize){
    final double[] coords = new double[(int) (curve.getN() / stepSize)];
    for(int i = 0; i < curve.getN() / stepSize; i++){
      coords[i] = curve.value(i * stepSize);
    }
    return coords;
  }

  private static void drawCurvedPath(Graphics2D graphics, Point[] points, MapPanel view){
    final double[] index = getIndex(points);
    final float stepSize = 0.01f;//TODO calculating a step size that makes sense
    final PolynomialSplineFunction xcurve = splineInterpolator.interpolate(index, pointsXToDoubleArray(points));
    final PolynomialSplineFunction ycurve = splineInterpolator.interpolate(index, pointsYToDoubleArray(points));
    final double[] xcoords = getCoords(xcurve, stepSize);
    final double[] ycoords = getCoords(ycurve, stepSize);

    for(int i = 1; i < xcoords.length; i++){
      //TODO maybe a line is not the best way to draw this...
      drawLineWithTranslate(graphics, new Line2D.Double(xcoords[i-1], ycoords[i-1], xcoords[i], ycoords[i]), view.getXOffset(), view.getYOffset());
    }
  }
}

Идея заключается в том, что, поскольку Spline Interpolator принимает только функции (например, f(x) = y), а x должен увеличиваться, мы разбиваем массив точек на 2 двойных массива и интерполируем эти 2 раза...
Сначала значения X, затем значения Y...
В качестве значений X берется "фиктивный массив", называемый "индексом", где первое значение равно 0, второе 1 - третье 2 и т. Д.
Чтобы нарисовать этот путь, я рисую линию от точки 0 до 1, от 1 до 2, от 2 до 3 и так далее...

Есть 2 вещи для рассмотрения...

1. Имеет ли смысл выбирать 1 в качестве размера шага в индексе? Это может привести к неточностям, так как java double имеет только 64 бита, и мы растягиваем и сжимаем значения с нашим статическим размером в 1 шаг. И если так, что я мог бы изменить, чтобы оптимизировать это...
2. И во-вторых, как можно лучше нарисовать эти 2 двойных массива? моя попытка нарисовать несколько линий выглядит не очень хорошо - это потому, что я читаю интерполированные значения слишком большими шагами?

Любая помощь очень ценится

РЕДАКТИРОВАТЬ:

Answer 1

Выбор 1 в качестве размера шага для массива index является так называемой равномерной параметризацией, которая, как правило, не приведет к хорошему результату, если ваши точки данных также не распределены относительно равномерно. Я бы рекомендовал использовать либо параметризацию по длине хорды, либо центростремительную параметризацию, как показано ниже:

t0 = 0.0
t1 = d1/L
t2 = t1 + d2/L  
t3 = t2 + d3/L
............
t(n-1)= 1.0.

где

d1=|P1-P0|^e, d2=|P2-P1|^e, d3=|P3-P2|^e and L = d1+d2+d3+.....d(n-1). 

Для параметризации длины хорды используйте e=1.0 в приведенной выше формуле. Для центростремительной параметризации используйте e=0,5. Обратите внимание, что использование e=0.0 просто приведет к равномерной параметризации. Если ваша точка данных имеет очень неравномерное распределение (то есть некоторые расстояния между точками огромны, а некоторые малы), центростремительная параметризация часто приводит к лучшему результату, чем параметризация по длине хорды.