Нахождение периодичности в алгоритмическом сигнале
При тестировании гипотезы о следующем рекурсивном соотношении
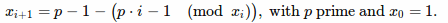 ,
,
который требует некоторой периодичности для последовательности чисел, я написал программу на python, которая вычисляет последовательности и печатает их в виде таблицы.
1 # Consider the recursive relation x_{i+1} = p-1 - (p*i-1 mod x_i)
2 # with p prime and x_0 = 1. What is the shortest period of the
3 # sequence?
4
5 from __future__ import print_function
6 import numpy as np
7 from matplotlib import pyplot as plt
8
9 # The length of the sequences.
10 seq_length = 100
11
12 upperbound_primes = 30
13
14 # Computing a list of prime numbers up to n
15 def primes(n):
16 sieve = [True] * n
17 for i in xrange(3,int(n**0.5)+1,2):
18 if sieve[i]:
19 sieve[i*i::2*i]=[False]*((n-i*i-1)/(2*i)+1)
20 return [2] + [i for i in xrange(3,n,2) if sieve[i]]
21
22 # The list of prime numbers up to upperbound_primes
23 p = primes(upperbound_primes)
24
25 # The amount of primes numbers
26 no_primes = len(p)
27
28 # Generate the sequence for the prime number p
29 def sequence(p):
30 x = np.empty(seq_length)
31 x[0] = 1
32 for i in range(1,seq_length):
33 x[i] = p - 1 - (p * (i-1) - 1) % x[i-1]
34 return x
35
36 # List with the sequences.
37 seq = [sequence(i) for i in p]
38 """
39 # Print the sequences in a table where the upper row
40 # indicates the prime numbers.
41 for i in range(seq_length):
42 if not i:
43 for n in p:
44 print('\t',n,end='')
45 print('')
46 print(i+1,'\t',end='')
47 for j in range(no_primes):
48 print(seq[j][i],end='\t')
49 print('\n',end='')
50 """
51 def autocor(x):
52 result = np.correlate(x,x,mode='full')
53 return result[result.size/2:]
54
55
56 fig = plt.figure('Finding period in the sequences')
57 k = 0
58 for s in seq:
59 k = k + 1
60 fig.add_subplot(no_primes,1,k)
61 plt.title("Prime number %d" % p[k-1])
62 plt.plot(autocor(s))
63 plt.show()
64
Теперь я хочу исследовать периодичности в этих последовательностях, которые я вычислил. Посмотрев в интернете, я обнаружил, что есть два варианта:
- Преформируйте автокорреляцию по данным и ищите первый пик. Это должно дать приблизительное значение периода.
- Предварительно БПФ на данных. Это показывает частоту чисел. Я не вижу, как это может дать какую-либо полезную информацию о периодичности последовательности чисел.
Последние строки показывают мою попытку использования автокорреляции, вдохновленную принятым ответом Как я могу использовать numpy.correlate для выполнения автокорреляции?,
Это дает следующий сюжет
 Ясно, что мы видим нисходящую последовательность чисел для всех простых чисел.
Ясно, что мы видим нисходящую последовательность чисел для всех простых чисел.
При тестировании того же метода на функции sin с помощью следующего простого кода кода Python
1 # Testing the autocorrelation of numpy
2
3 import numpy as np
4 from matplotlib import pyplot as plt
5
6 num_samples = 1000
7 t = np.arange(num_samples)
8 dt = 0.1
9
10 def autocor(x):
11 result = np.correlate(x,x,mode='full')
12 return result[result.size/2:]
13
14 def f(x):
15 return [np.sin(i * 2 * np.pi * dt) for i in range(num_samples)]
16
17 plt.plot(autocor(f(t)))
18 plt.show()
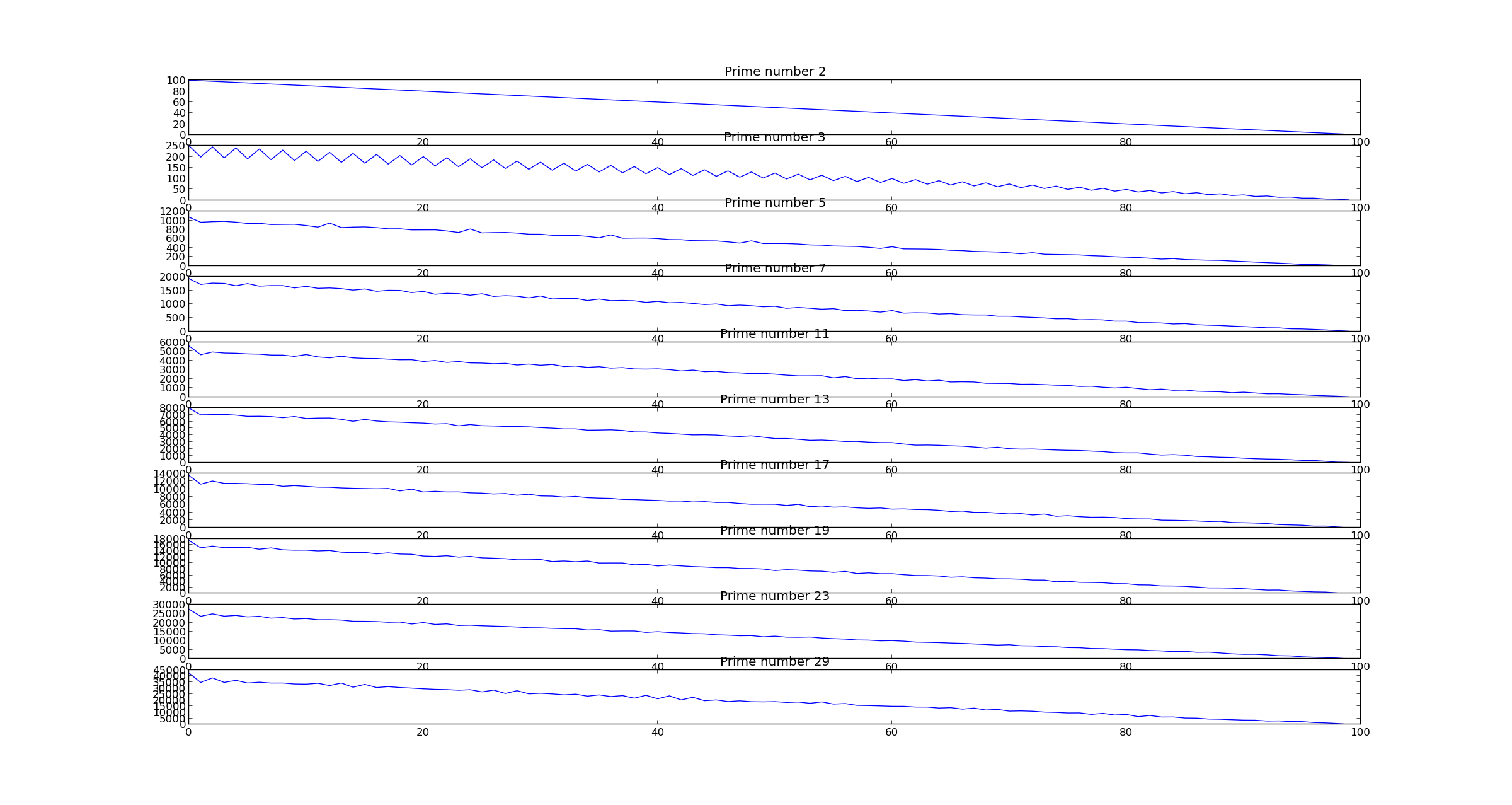
Я получаю аналогичный результат, он дает следующий график для функции синуса
Например, как я могу считать периодичность в случае синусоидальной функции?
Во всяком случае, я не понимаю механизм автокорреляции, приводящей к пикам, которые дают информацию о периодичности сигнала. Кто-нибудь может уточнить это? Как правильно использовать автокорреляцию в этом контексте?
И что я делаю не так в своей реализации автокорреляции?
Предложения по альтернативным методам определения периодичности в последовательности чисел приветствуются.
2 ответа
Здесь довольно много вопросов, поэтому я начну описывать, как автокорреляция создает период из случая "3", т. Е. Ваш второй подзаговор первого изображения.
Для простого числа 3 последовательность (после менее последовательного начала) 1,2,1,2,1,2,1,2,..., Чтобы вычислить автокорреляцию, массив в основном переводится относительно самого себя, все выравнивающие элементы умножаются, и все эти результаты добавляются. Так выглядит примерно так, для нескольких тестовых случаев, где A это автокорреляция:
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 1
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 1
1 4 1 4 1 4 1 4 4 1 4 1 4 1 4 # products
# above result A[0] = 5*25 5=1+4 25=# of pairs # A[0] = 125
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 1
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 1
2 2 2 2 2 2 2 2 2 2 2 2 2 2 # products
# above result A[1] = 4*24 4=2+2 24=# of pairs # A[1] = 96
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 0
1 2 1 2 1 2 1 2 2 1 2 1 2 1 2 # values 1
0 1 2 3 4 5 6 7 ... 43 44 45 46 47 48 49 # indices 1
1 4 1 4 1 4 1 4 4 1 4 1 4 # products
# above result A[2] = 5*23 5=4+1 23=# of pairs # A[2] = 115
Из приведенного выше есть три сообщения: 1. автокорреляция, A, имеет большее значение, когда подобные элементы выстроены в ряд и умножены, здесь на каждом другом шаге. 2. Индекс автокорреляции соответствует относительному сдвигу. 3. При выполнении автокорреляции для полных массивов, как показано здесь, всегда происходит нисходящее линейное изменение, поскольку количество точек, складываемых вместе для получения значения, уменьшается при каждом последующем сдвиге.
Итак, здесь вы можете увидеть, почему на вашем графике есть периодическое увеличение на 20% от "простого числа 3": потому что суммы, которые суммируются, равны 1+4, когда они выровнены, против 2+2, когда они не равны, то есть 5 против 4. Именно этот удар, который вы ищете в чтении периода. То есть вот показывает, что период 2, так как это индекс вашего первого удара. (Кроме того, обратите внимание, что в приведенном выше примере я делаю вычисления только как количество пар, чтобы увидеть, как эта известная периодичность приводит к результату, который вы видите в автокорреляции, то есть вообще не нужно думать о количестве пар.)
В этих вычислениях значения удара относительно базы будут увеличены, если вы сначала вычтете среднее значение перед выполнением автокорреляции. Рампа может быть удалена, если вы выполняете расчеты с использованием массивов с обрезанными концами, поэтому перекрытие всегда одинаковое; это обычно имеет смысл, поскольку обычно нужно искать периодичность значительно меньшей длины волны, чем полная выборка (потому что для определения хорошего периода колебаний требуется много колебаний).
Для автокорреляции синусоидальной волны основной ответ заключается в том, что период показан как первый удар. Я переделал сюжет за исключением примененной оси времени. В этих вещах всегда яснее использовать ось реального времени, поэтому я немного изменил ваш код, чтобы включить это. (Кроме того, я заменил понимание списка на правильное векторизованное числовое выражение для вычисления волны синуса, но здесь это не важно. И я также явно определил частоту в f(x), просто чтобы было более понятно, что происходит - как неявная частота 1 в замешательстве.)
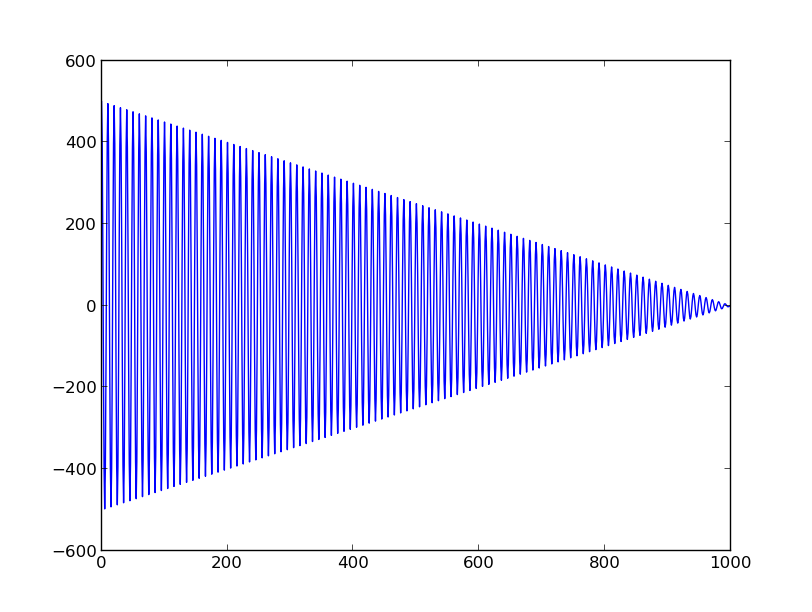
Суть в том, что, поскольку автокорреляция рассчитывается путем смещения вдоль оси по одной точке за раз, ось автокорреляции является только осью времени. Таким образом, я строю это как ось, а затем могу считать период от этого. Здесь я увеличил масштаб, чтобы увидеть это ясно (и код ниже):
# Testing the autocorrelation of numpy
import numpy as np
from matplotlib import pyplot as plt
num_samples = 1000
dt = 0.1
t = dt*np.arange(num_samples)
def autocor(x):
result = np.correlate(x,x,mode='full')
return result[result.size/2:]
def f(freq):
return np.sin(2*np.pi*freq*t)
plt.plot(t, autocor(f(.3)))
plt.xlabel("time (sec)")
plt.show()
То есть в приведенном выше, я установил частоту 0.3и график показывает период как о 3.3что и ожидается.
Все это говорит, по моему опыту, автокорреляция обычно работает хорошо для физических сигналов, но не так надежно для алгоритмических сигналов. Например, довольно легко сбросить, если периодический сигнал пропускает шаг, что может случиться с алгоритмом, но менее вероятно с вибрирующим объектом. Вы могли бы подумать, что вычислять этот период алгоритмического сигнала должно быть тривиально, но небольшой поиск покажет, что это не так, и даже трудно определить, что подразумевается под периодом. Например, серия:
1 2 1 2 1 2 0 1 2 1 2 1 2
не будет хорошо работать с автокорреляционным тестом.
Обновить.
@ tom10 дал подробный обзор автокорреляции и объяснил, почему первый удар в автокорреляции может дать период периодического сигнала.
Я пробовал оба подхода, FFT, а также автокорреляцию. Их результаты совпадают, хотя я бы предпочел БПФ, а не автокорреляцию, поскольку он дает вам период более прямо.
При использовании автокорреляции мы просто определяем координату первого пика. Ручная проверка графика автокорреляции покажет, есть ли у вас "правильный" пик, поскольку вы можете заметить период (хотя для простых чисел выше 7 это становится менее ясным). Я уверен, что вы могли бы также разработать простой алгоритм, который вычисляет "правильный" пик. Возможно, кто-то мог бы остановиться на каком-то простом алгоритме, который делает эту работу?
См., Например, следующий график последовательностей рядом с их автокорреляцией. 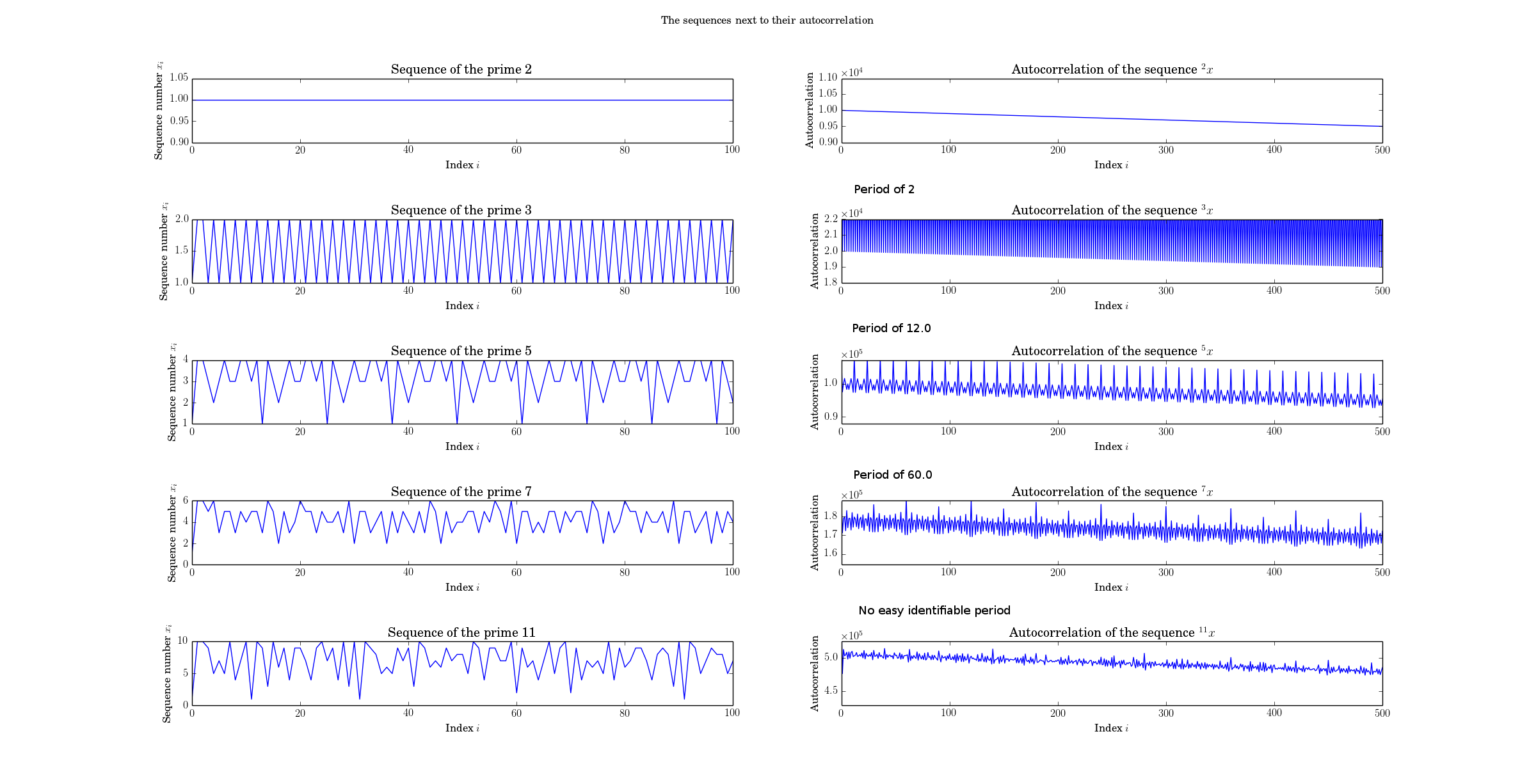 Код:
Код:
1 # Plotting sequences satisfying, x_{i+1} = p-1 - (p*i-1 mod x_i)
2 # with p prime and x_0 = 1, next to their autocorrelation.
3
4 from __future__ import print_function
5 import numpy as np
6 from matplotlib import pyplot as plt
7
8 # The length of the sequences.
9 seq_length = 10000
10
11 upperbound_primes = 12
12
13 # Computing a list of prime numbers up to n
14 def primes(n):
15 sieve = [True] * n
16 for i in xrange(3,int(n**0.5)+1,2):
17 if sieve[i]:
18 sieve[i*i::2*i]=[False]*((n-i*i-1)/(2*i)+1)
19 return [2] + [i for i in xrange(3,n,2) if sieve[i]]
20
21 # The list of prime numbers up to upperbound_primes
22 p = primes(upperbound_primes)
23
24 # The amount of primes numbers
25 no_primes = len(p)
26
27 # Generate the sequence for the prime number p
28 def sequence(p):
29 x = np.empty(seq_length)
30 x[0] = 1
31 for i in range(1,seq_length):
32 x[i] = p - 1 - (p * (i-1) - 1) % x[i-1]
33 return x
34
35 # List with the sequences.
36 seq = [sequence(i) for i in p]
37
38 # Autocorrelation function.
39 def autocor(x):
40 result = np.correlate(x,x,mode='full')
41 return result[result.size/2:]
42
43 fig = plt.figure("The sequences next to their autocorrelation")
44 plt.suptitle("The sequences next to their autocorrelation")
45
46 # Proper spacing between subplots.
47 fig.subplots_adjust(hspace=1.2)
48
49 # Set up pyplot to use TeX.
50 plt.rc('text',usetex=True)
51 plt.rc('font',family='serif')
52
53 # Maximize plot window by command.
54 mng = plt.get_current_fig_manager()
55 mng.resize(*mng.window.maxsize())
56
57 k = 0
58 for s in seq:
59 k = k + 1
60 fig.add_subplot(no_primes,2,2*(k-1)+1)
61 plt.title("Sequence of the prime %d" % p[k-1])
62 plt.plot(s)
63 plt.xlabel(r"Index $i$")
64 plt.ylabel(r"Sequence number $x_i$")
65 plt.xlim(0,100)
66
67 # Constrain the number of ticks on the y-axis, for clarity.
68 plt.locator_params(axis='y',nbins=4)
69
70 fig.add_subplot(no_primes,2,2*k)
71 plt.title(r"Autocorrelation of the sequence $^{%d}x$" % p[k-1])
72 plt.plot(autocor(s))
73 plt.xlabel(r"Index $i$")
74 plt.xticks
75 plt.ylabel("Autocorrelation")
76
77 # Proper scaling of the y-axis.
78 ymin = autocor(s)[1]-int(autocor(s)[1]/10)
79 ymax = autocor(s)[1]+int(autocor(s)[1]/10)
80 plt.ylim(ymin,ymax)
81 plt.xlim(0,500)
82
83 plt.locator_params(axis='y',nbins=4)
84
85 # Use scientific notation when 0< t < 1 or t > 10
86 plt.ticklabel_format(style='sci',axis='y',scilimits=(0,1))
87
88 plt.show()
При использовании БПФ мы преобразовываем нашу последовательность Фурье и ищем первый пик. Координата этого первого пика дает самую грубую частоту, которая представляет наш сигнал. Это даст наш период, поскольку самая грубая частота - это частота, с которой наша последовательность (в идеале) колеблется.
Смотрите следующий график последовательностей рядом с их преобразованиями Фурье.
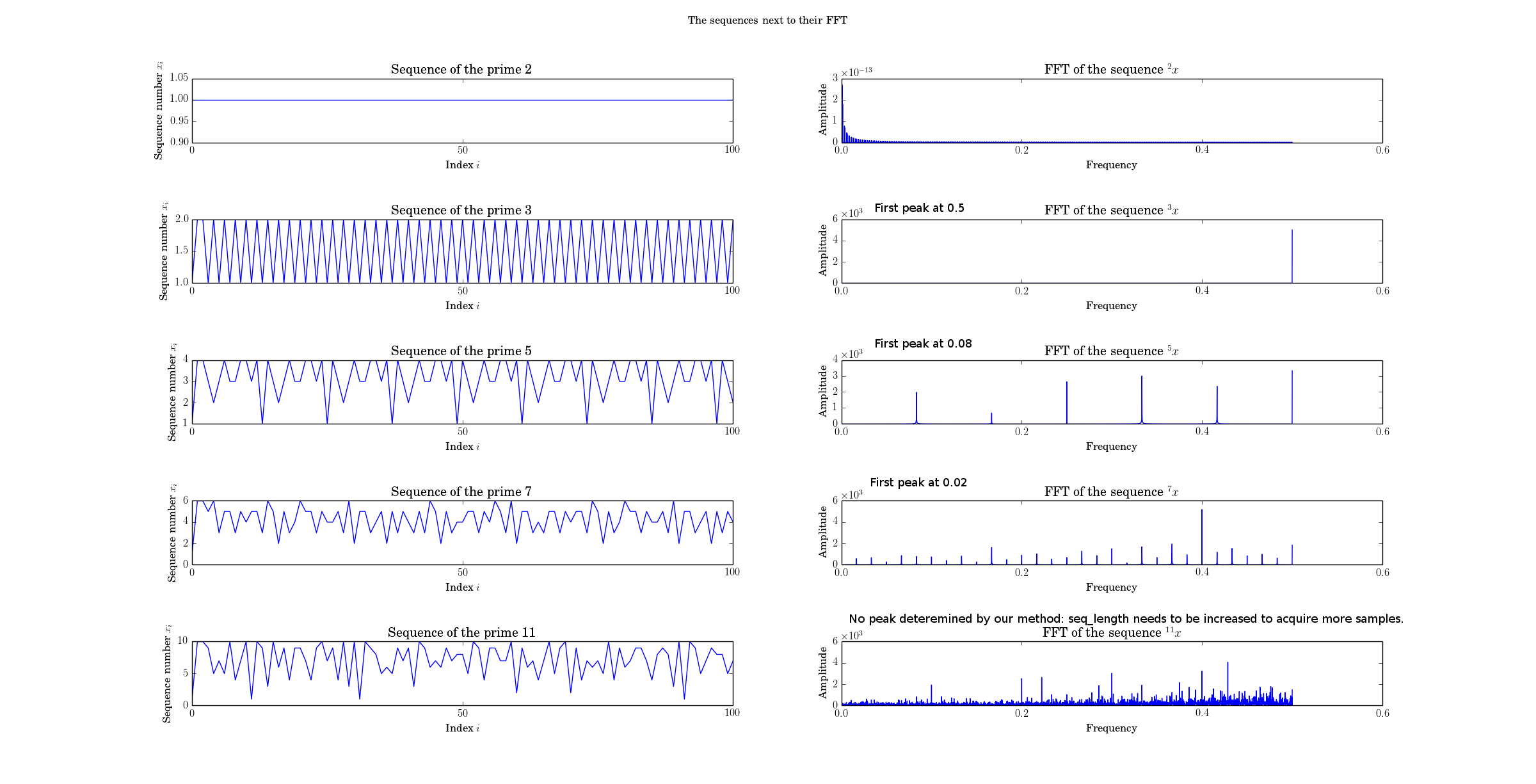
Код:
1 # Plotting sequences satisfying, x_{i+1} = p-1 - (p*i-1 mod x_i)
2 # with p prime and x_0 = 1, next to their Fourier transforms.
3
4 from __future__ import print_function
5 import numpy as np
6 from matplotlib import pyplot as plt
7
8 # The length of the sequences.
9 seq_length = 10000
10
11 upperbound_primes = 12
12
13 # Computing a list of prime numbers up to n
14 def primes(n):
15 sieve = [True] * n
16 for i in xrange(3,int(n**0.5)+1,2):
17 if sieve[i]:
18 sieve[i*i::2*i]=[False]*((n-i*i-1)/(2*i)+1)
19 return [2] + [i for i in xrange(3,n,2) if sieve[i]]
20
21 # The list of prime numbers up to upperbound_primes
22 p = primes(upperbound_primes)
23
24 # The amount of primes numbers
25 no_primes = len(p)
26
27 # Generate the sequence for the prime number p
28 def sequence(p):
29 x = np.empty(seq_length)
30 x[0] = 1
31 for i in range(1,seq_length):
32 x[i] = p - 1 - (p * (i-1) - 1) % x[i-1]
33 return x
34
35 # List with the sequences.
36 seq = [sequence(i) for i in p]
37
38 fig = plt.figure("The sequences next to their FFT")
39 plt.suptitle("The sequences next to their FFT")
40
41 # Proper spacing between subplots.
42 fig.subplots_adjust(hspace=1.2)
43
44 # Set up pyplot to use TeX.
45 plt.rc('text',usetex=True)
46 plt.rc('font',family='serif')
47
48
49 # Maximize plot window by command.
50 mng = plt.get_current_fig_manager()
51 mng.resize(*mng.window.maxsize())
52
53 k = 0
54 for s in seq:
55 f = np.fft.rfft(s)
56 f[0] = 0
57 freq = np.fft.rfftfreq(seq_length)
58 k = k + 1
59 fig.add_subplot(no_primes,2,2*(k-1)+1)
60 plt.title("Sequence of the prime %d" % p[k-1])
61 plt.plot(s)
62 plt.xlabel(r"Index $i$")
63 plt.ylabel(r"Sequence number $x_i$")
64 plt.xlim(0,100)
65
66 # Constrain the number of ticks on the y-axis, for clarity.
67 plt.locator_params(nbins=4)
68
69 fig.add_subplot(no_primes,2,2*k)
70 plt.title(r"FFT of the sequence $^{%d}x$" % p[k-1])
71 plt.plot(freq,abs(f))
72 plt.xlabel("Frequency")
73 plt.ylabel("Amplitude")
74 plt.locator_params(nbins=4)
75
76 # Use scientific notation when 0 < t < 0 or t > 10
77 plt.ticklabel_format(style='sci',axis='y',scilimits=(0,1))
78
79 plt.show()
Чтобы понять, почему метод БПФ более удобен, чем автокорреляция, обратите внимание на то, что у нас есть четкий алгоритм определения периода: найдите первый пик преобразования Фурье. Для достаточного количества образцов это всегда работает.
См. Следующую таблицу, полученную методом FFT, который согласуется с методом автокорреляции.
prime frequency period
2 0.00 1000.00
3 0.50 2.00
5 0.08 12.00
7 0.02 59.88
11 0.00 1000.00
Следующий код реализует алгоритм, распечатывая таблицу с указанием частоты и периода последовательностей на простое число.
1 # Print a table of periods, determined by the FFT method,
2 # of sequences satisfying,
3 # x_{i+1} = p-1 - (p*i-1 mod x_i) with p prime and x_0 = 1.
4
5 from __future__ import print_function
6 import numpy as np
7 from matplotlib import pyplot as plt
8
9 # The length of the sequences.
10 seq_length = 10000
11
12 upperbound_primes = 12
13
14 # Computing a list of prime numbers up to n
15 def primes(n):
16 sieve = [True] * n
17 for i in xrange(3,int(n**0.5)+1,2):
18 if sieve[i]:
19 sieve[i*i::2*i]=[False]*((n-i*i-1)/(2*i)+1)
20 return [2] + [i for i in xrange(3,n,2) if sieve[i]]
21
22 # The list of prime numbers up to upperbound_primes
23 p = primes(upperbound_primes)
24
25 # The amount of primes numbers
26 no_primes = len(p)
27
28 # Generate the sequence for the prime number p
29 def sequence(p):
30 x = np.empty(seq_length)
31 x[0] = 1
32 for i in range(1,seq_length):
33 x[i] = p - 1 - (p * (i-1) - 1) % x[i-1]
34 return x
35
36 # List with the sequences.
37 seq = [sequence(i) for i in p]
38
39 # Function that finds the first peak.
40 # Assumption: seq_length >> 10 so the Fourier transformed
41 # signal is sufficiently smooth.
42 def firstpeak(x):
43 for i in range(10,len(x)-1):
44 if x[i+1] < x[i]:
45 return i
46 return len(x)-1
47
48 k = 0
49 for s in seq:
50 f = np.fft.rfft(s)
51 freq = np.fft.rfftfreq(seq_length)
52 k = k + 1
53 if k == 1:
54 print("prime \t frequency \t period")
55 print(p[k-1],'\t %.2f' % float(freq[firstpeak(abs(f))]), \
56 '\t\t %.2f' % float(1/freq[firstpeak(abs(f))]))
Я использовал 10000 образцов (seq_length) во всем приведенном выше коде. При увеличении количества выборок видно, что периоды сходятся к определенному интегральному значению (с использованием метода БПФ).
Метод БПФ кажется мне идеальным инструментом для определения периодов в алгоритмических сигналах, один из которых ограничен только количеством образцов, которое может обрабатывать ваше оборудование.