Выход KISS FFT с или без окон

Question

В настоящее время я пытаюсь внедрить fft в микроконтроллеры avr32 для обработки сигналов с помощью kiss fft. И возникли странные проблемы с моим выводом. По сути, я передаю образцы АЦП (тестирование с помощью генератора функций) в fft (реальный ввод, размер 256 n), и полученный вывод имеет смысл для меня. Однако, если я применяю окно Хэмминга к выборкам АЦП, а затем передаю их в БПФ, частотный интервал пиковой величины является неправильным (и отличается от предыдущего результата без использования окон). Сэмплы АЦП имеют смещение постоянного тока, поэтому я устранил смещение, но оно не работает с сэмплами с окнами.

Ниже приведены первые несколько выходных значений через RS485. Первый столбец - это вывод fft без окна, тогда как второй столбец - это вывод с окном. Из столбца 1 пик в строке 6 (6 x fs (10,5 кГц) / 0,5N) дал мне правильный результат входной частоты, где столбец 2 имеет пиковую величину в строке 2 (кроме постоянного тока), что не имеет смысла для меня, Любое предложение будет полезно. Заранее спасибо.

    488 260 // Контейнер постоянного тока 5            97
    5            41
    5            29  
    4            26
    10           35
    133          76
    33           28
    21           6
    17           3

kiss_fft_scalar zero;
memset(&zero,0,sizeof(zero));
kiss_fft_cpx fft_input[n];
kiss_fft_cpx fft_output[n];

for(ctr=0; ctr<n; ctr++)
{
    fft_input[ctr].r = zero;
    fft_input[ctr].i = zero;
    fft_output[ctr].r =zero;
    fft_output[ctr].i = zero;
}

// IIR filter calculation

for (ctr=0; ctr<n; ctr++)
{       
    // filter calculation
    y[ctr] = num_coef[0]*x[ctr];

    y[ctr] += (num_coef[1]*x[ctr-1]) - (den_coef[1]*y[ctr-1]);
    y[ctr] += (num_coef[2]*x[ctr-2]) - (den_coef[2]*y[ctr-2]);
    //y1[ctr] += y[ctr] - 500;
    // hamming window
    hamming[ctr] = (0.54-((0.46) * cos(2*PI*ctr/256)));
    window[ctr] = hamming[ctr]*y[ctr];

    fft_input[ctr].r = window[ctr];
    fft_input[ctr].i = 0;
    fft_output[ctr].r = 0;
    fft_output[ctr].i = 0;

}

kiss_fftr_cfg fftConfig = kiss_fftr_alloc(n,0,NULL,NULL);
kiss_fftr(fftConfig, (kiss_fft_scalar * )fft_input, fft_output);


for (ctr=0; ctr<n; ctr++)
{   
    fft_mag[ctr] = (sqrt((fft_output[ctr].r * fft_output[ctr].r) + (fft_output[ctr].i * fft_output[ctr].i)))/(0.5*n);

    //Usart write
    char filtResult[10];
    sprintf(filtResult, "%04d %04d\n", (int)x[ctr], (int)fft_mag[ctr]);
    //sprintf(filtResult, "%04d %04d\n", (int)x[ctr], (int)window[ctr]);
    char c;
    char *ptr = &filtResult[0];
    do
    {   
        c = *ptr;
        ptr++;
        usart_bw_write_char(&AVR32_USART2, (int)c);
        // sendByte(c);

    } while (c != '\n');
}

kiss_fft_cleanup();
free(fftConfig);        

Answer 1

Уточнения выходной частотной области

В частотной области прямоугольные окна и окна Хэмминга выглядят так:

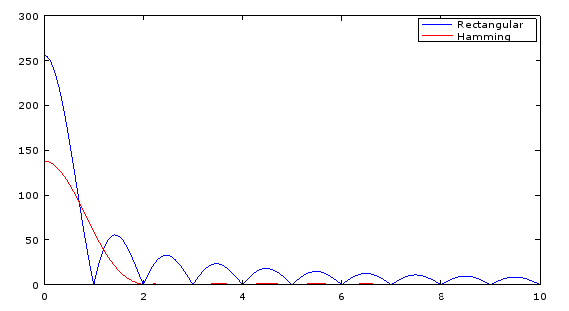
Как вы, возможно, знаете, умножение во временной области на окно соответствует свертке в частотной области, которая по существу распределяет энергию сигнала по нескольким частотным бинам в так называемой спектральной утечке. Для конкретных окон, которые вы выбрали (как показано выше в частотной области), вы можете заметить, что окно Хемминга распространяет гораздо меньше энергии за пределами основного лепестка, но этот главный лепесток немного шире, чем у прямоугольного окна.

В результате всплеск энергии постоянного тока заканчивается распространением за ячейку 0 и в ячейку 1 при использовании окна Хэмминга. Это не так много, что у вас есть сильный пик в бине 1. На самом деле, если вы наносите на график предоставленные вами данные, вы должны увидеть, что всплеск, который вы видели в индексе 6, на самом деле все еще там на той же частоте с и без использования окна Хемминга:

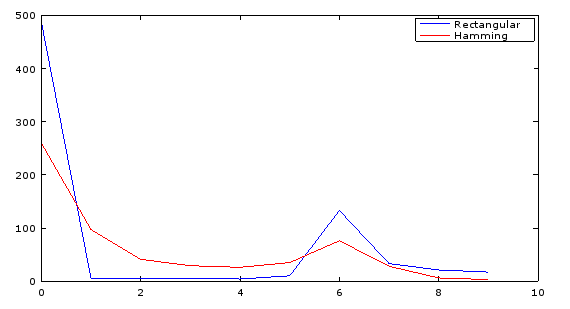
Если вы хотите избавиться от всплеска постоянного тока и утечки в окружающих бинах, либо удалите смещение в ваших данных (по существу, применив режекторный фильтр), либо вам придется игнорировать еще несколько низкочастотных бинов при поиске вашего " первый сильный скачок ".

Фильтрация проблемы

Наконец, обратите внимание, что есть также проблема с тем, как реализован фильтр IIR, из-за которого массивы x а также y будет проиндексирован вне границ, когда ctr==0 а также ctr==1 (если вы не сделали какое-то специальное положение и x & y фактически являются указателями со смещением от начала выделенных буферов). Это может повлиять на результаты как с окном, так и без него. Если вы фильтруете только один блок данных, распространенным предположением является то, что более ранние выборки были нулями. В этом случае вы можете избежать внешней индексации с помощью:

// filter calculation
y[ctr] = num_coef[0]*x[ctr];

if (ctr>=1)
{
  y[ctr] += (num_coef[1]*x[ctr-1]) - (den_coef[1]*y[ctr-1]);
}
if (ctr>=2)
{
  y[ctr] += (num_coef[2]*x[ctr-2]) - (den_coef[2]*y[ctr-2]);
}

Если, с другой стороны, вы хотите отфильтровать несколько блоков n сэмплы, вам нужно запомнить последние несколько сэмплов из предыдущего блока. Это может быть сделано путем выделения буферов, которые немного больше, чем размер блока:

x = malloc((n+2)*sizeof(kiss_fft_scalar));
y = malloc((n+2)*sizeof(kiss_fft_scalar));
// initialize "past samples" for the first block, assuming data was zero
x[0] = x[1] = 0;
y[0] = y[1] = 0;

Тогда вы можете использовать смещение в этих буферах. Индексы 0 и 1 представляют прошедшие выборки, тогда как остальная часть буфера из индекса 2 заполняется текущим блоком входных данных. Это приводит к следующему слегка измененному фильтрующему коду:

// filter calculation
y[ctr+2] = num_coef[0]*x[ctr+2];

y[ctr+2] += (num_coef[1]*x[ctr+1]) - (den_coef[1]*y[ctr+1]);
y[ctr+2] += (num_coef[2]*x[ctr]) - (den_coef[2]*y[ctr]);

// hamming window
hamming[ctr] = (0.54-((0.46) * cos(2*PI*ctr/256)));
window[ctr] = hamming[ctr]*y[ctr+2];

Наконец, в конце каждого блока вам необходимо обновить "прошлые выборки" с индексами 0 и 1, чтобы последние выборки текущего блока были готовы обработать следующий входной блок:

// remember last 2 samples of block
x[0] = x[n-2];
x[1] = x[n-1];
y[0] = y[n-2];
y[1] = y[n-1];