Почему мы должны нормализовать ввод для искусственной нейронной сети?
Это принципиальный вопрос, касающийся теории нейронных сетей:
Почему мы должны нормализовать вход для нейронной сети?
Я понимаю, что иногда, когда, например, входные значения не числовые, необходимо выполнить определенное преобразование, но когда у нас есть числовой ввод? Почему цифры должны быть в определенном интервале?
Что будет, если данные не нормализуются?
10 ответов
Это хорошо объяснено здесь.
Если входные переменные объединяются линейно, как в MLP, то редко требуется строго стандартизировать входные данные, по крайней мере, теоретически. Причина в том, что любое изменение масштаба входного вектора может быть эффективно отменено путем изменения соответствующих весов и смещений, в результате чего вы получите те же выходные данные, что и раньше. Тем не менее, существует множество практических причин, по которым стандартизация входных данных может ускорить обучение и снизить шансы застрять в локальных оптимумах. Кроме того, снижение веса и байесовскую оценку можно сделать более удобно с помощью стандартизированных входных данных.
В нейронных сетях рекомендуется не только нормализовать данные, но и масштабировать их. Это предназначено для более быстрого приближения к глобальным минимумам на поверхности ошибки. Смотрите следующие фотографии: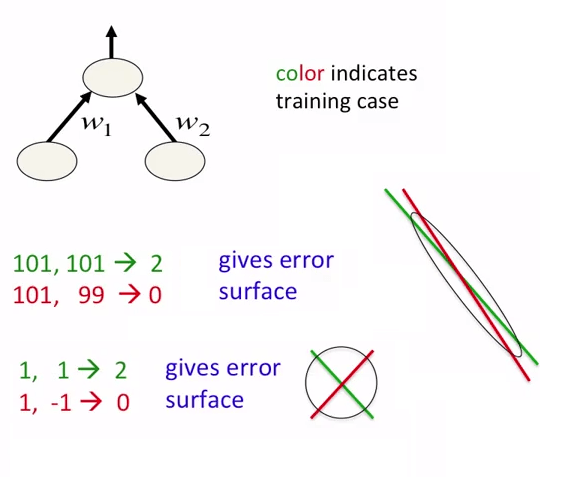
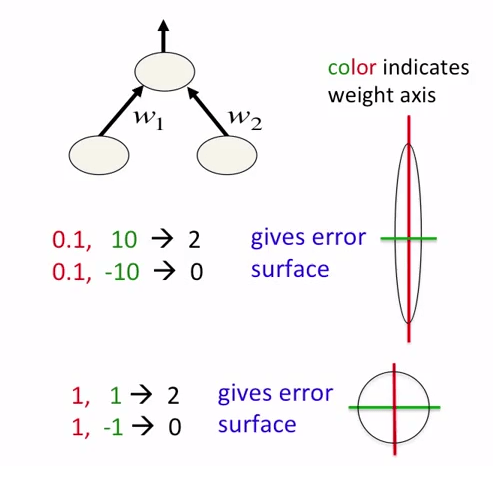
Фотографии взяты из курса курса о нейронных сетях. Автор курса - Джеффри Хинтон.
Некоторые входные данные для NN могут не иметь "естественно определенного" диапазона значений. Например, среднее значение может медленно, но непрерывно увеличиваться с течением времени (например, количество записей в базе данных).
В таком случае подача этого необработанного значения в вашу сеть будет работать не очень хорошо. Вы научите свою сеть значениям из нижней части диапазона, в то время как фактические входные данные будут из верхней части этого диапазона (и, возможно, выше диапазона, с которым сеть научилась работать).
Вы должны нормализовать это значение. Например, вы можете сказать сети, насколько изменилось значение с момента предыдущего ввода. Этот прирост обычно можно определить с высокой вероятностью в определенном диапазоне, что делает его хорошим входом для сети.
Есть 2 причины, по которым мы должны нормализовать входные функции, прежде чем передавать их в нейронную сеть:
Причина 1: ЕслиFeature в Dataset является большим по масштабу по сравнению с другими, тогда эта крупномасштабная функция становится доминирующей, и в результате прогнозы нейронной сети не будут точными.
Пример: в случае данных о сотрудниках, если мы рассматриваем возраст и зарплату, возраст будет двузначным числом, а зарплата может быть 7- или 8-значным (1 миллион и т. Д.). В этом случае зарплата будет преобладать над прогнозом нейронной сети. Но если мы нормализуем эти функции, значения обеих функций будут находиться в диапазоне от (0 до 1).
Причина 2: Переднее распространение нейронных сетей включает точечное произведение весов с входными характеристиками. Итак, если значения очень высокие (для данных изображений и не изображений), вычисление вывода занимает много времени вычислений, а также памяти. То же самое и во время обратного распространения. Следовательно, модель сходится медленно, если входные данные не нормализованы.
Пример: если мы выполним классификацию изображений, размер изображения будет очень большим, так как значение каждого пикселя находится в диапазоне от 0 до 255. Нормализация в этом случае очень важна.
Ниже перечислены случаи, когда нормализация очень важна:
- К-средние
- K-Ближайшие-соседи
- Анализ главных компонентов (PCA)
- Градиентный спуск
Когда вы используете ненормализованные входные объекты, функция потерь, вероятно, будет иметь очень удлиненные впадины. При оптимизации с градиентным спуском это становится проблемой, потому что градиент будет крутым по отношению к некоторым параметрам. Это приводит к большим колебаниям в пространстве поиска, когда вы подпрыгиваете между крутыми склонами. Чтобы компенсировать это, вам нужно стабилизировать оптимизацию с небольшой скоростью обучения.
Рассмотрим признаки x1 и x2, где диапазон от 0 до 1 и от 0 до 1 миллиона соответственно. Оказывается, отношения для соответствующих параметров (скажем, w1 и w2) тоже будут большими.
Нормализация делает функцию потерь более симметричной / сферической. Их легче оптимизировать, потому что градиенты имеют тенденцию указывать на глобальный минимум, и вы можете делать большие шаги.
Глядя на нейронную сеть снаружи, это просто функция, которая принимает некоторые аргументы и дает результат. Как и во всех функциях, он имеет домен (то есть набор юридических аргументов). Вы должны нормализовать значения, которые вы хотите передать в нейронную сеть, чтобы убедиться, что она находится в домене. Как и во всех функциях, если аргументы не находятся в домене, результат не гарантируется как соответствующий.
Точное поведение нейронной сети на аргументах вне домена зависит от реализации нейронной сети. Но в целом результат бесполезен, если аргументы находятся за пределами домена.
Я считаю, что ответ зависит от сценария.
Рассмотрим NN (нейронную сеть) как оператор F, так что F(вход) = выход. В случае, когда это отношение является линейным, так что F(A * input) = A * output, вы можете либо оставить ненормализованный ввод / вывод в их необработанных формах, либо нормализовать оба, чтобы исключить A. Очевидно, это предположение о линейности нарушается в задачах классификации или почти в любой задаче, которая выводит вероятность, где F(A * input) = 1 * output
На практике нормализация позволяет приспосабливать неадаптируемые сети, что крайне важно для экспериментаторов / программистов. Тем не менее, точное влияние нормализации будет зависеть не только от архитектуры / алгоритма сети, но также от статистического приоритета для ввода и вывода.
Более того, NN часто внедряется для решения очень сложных проблем способом "черного ящика", что означает, что основная проблема может иметь очень плохую статистическую формулировку, что затрудняет оценку влияния нормализации, приводя к техническому преимуществу (становясь пригодным) доминировать над его влиянием на статистику.
В статистическом смысле нормализация удаляет вариацию, которая, как считается, не является причинно-следственной в прогнозировании выходных данных, чтобы не допустить, чтобы NN изучал эту вариацию как предиктор (NN не видит эту вариацию, следовательно, не может использовать ее).
Причина, по которой нормализация необходима, заключается в том, что если вы посмотрите, как адаптивный шаг проходит в одном месте в области функции, и вы просто перенесете задачу в эквивалент того же шага, переведенного каким-то большим значением в некотором направлении в домен, то вы получите разные результаты. Это сводится к вопросу об адаптации линейной части к точке данных. Сколько должна двигаться фигура, не поворачиваясь, и сколько она должна поворачиваться в ответ на одну тренировку? Нет смысла менять процедуру адаптации в разных частях домена! Поэтому нормализация необходима для уменьшения разницы в тренировочном результате. Я не написал это, но вы можете просто взглянуть на математику для простой линейной функции и на то, как она обучается одной тренировочной точкой в двух разных местах. Эта проблема, возможно, была исправлена в некоторых местах, но я не знаком с ними. В ALN проблема была исправлена, и я могу выслать вам документ, если вы напишите wwarmstrong AT shaw.ca
На высоком уровне, если вы заметите, где в основном используется нормализация / стандартизация, вы заметите, что всякий раз, когда в процессе построения модели используется разность величин, возникает необходимость стандартизировать входные данные, чтобы гарантировать, что важные входные данные с небольшими масштабами не теряют своей значимости в середине процесса построения модели.
пример:
√(3-1)^2+(1000-900)^2 ≈ √(1000-900)^2
Здесь (3-1) практически не влияет на результат, и, следовательно, ввод, соответствующий этим значениям, считается бесполезным по модели.
Обратите внимание на следующее:
- При кластеризации используются евклидовы или другие меры расстояния.
- Сетевые сети используют алгоритм оптимизации для минимизации функции затрат (например, MSE).
Как мера расстояния (кластеризация), так и функция стоимости (NN) каким-то образом используют разницу величин, и, следовательно, стандартизация гарантирует, что разница величин не влияет на важные входные параметры, а алгоритм работает, как ожидалось.
Скрытые слои используются в соответствии со сложностью наших данных. Если у нас есть входные данные, которые являются линейно разделимыми, то нам не нужно использовать скрытый слой, например, вентиль ИЛИ, но если у нас есть нелинейно разделимые данные, то нам нужно использовать скрытый слой, например, логический вентиль ExOR. Количество узлов, взятых на любом слое, зависит от степени перекрестной проверки нашего вывода.