Алгоритм размещения сетки над неупорядоченным множеством точек

Question

Учитывая большой набор (от десятков тысяч до миллионов) неупорядоченных точек, представленных в виде трехмерных декартовых векторов, каков хороший алгоритм для создания правильной квадратной сетки (с заданным пользователем интервалом), которая охватывает все точки? Некоторые ограничения:

1. Сетка должна быть квадратной и правильной
2. Мне нужно иметь возможность регулировать интервал сетки (длина стороны одного из квадратов), в идеале с одной переменной
3. Мне нужна сетка минимального размера, т.е. каждый "блок" в сетке должен содержать хотя бы одну из неупорядоченных точек, и каждая неупорядоченная точка должна быть заключена в "блок"
4. Возвращаемым значением алгоритма должен быть список координат точек сетки

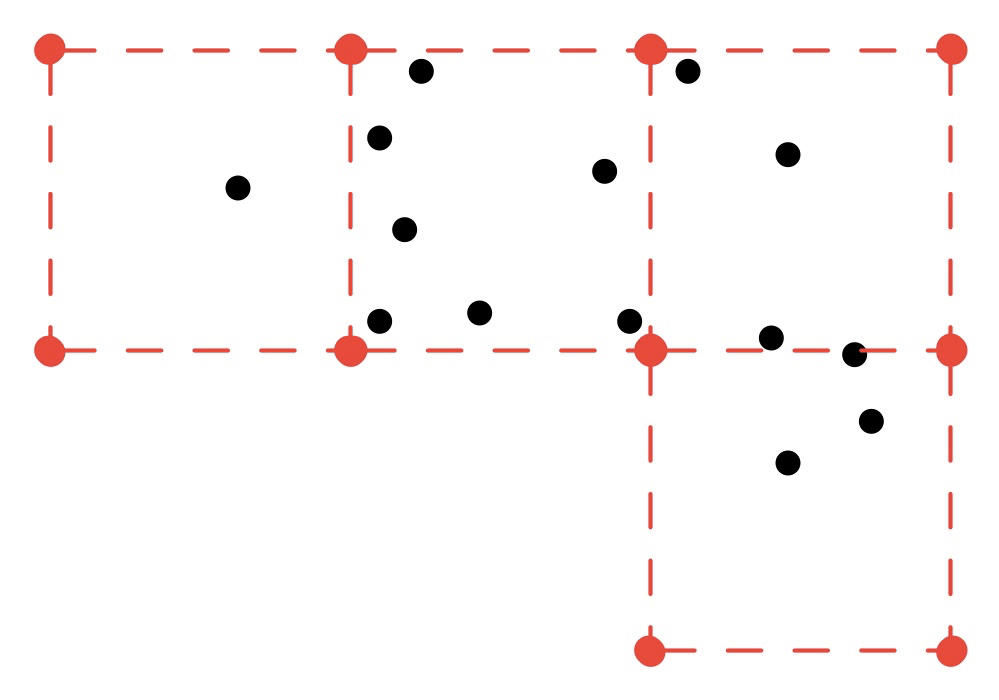
Для иллюстрации в 2D, учитывая этот набор точек:

для некоторого интервала сетки X одним возможным возвращаемым значением алгоритма будут координаты этих красных точек (пунктирные линии только для иллюстрации):

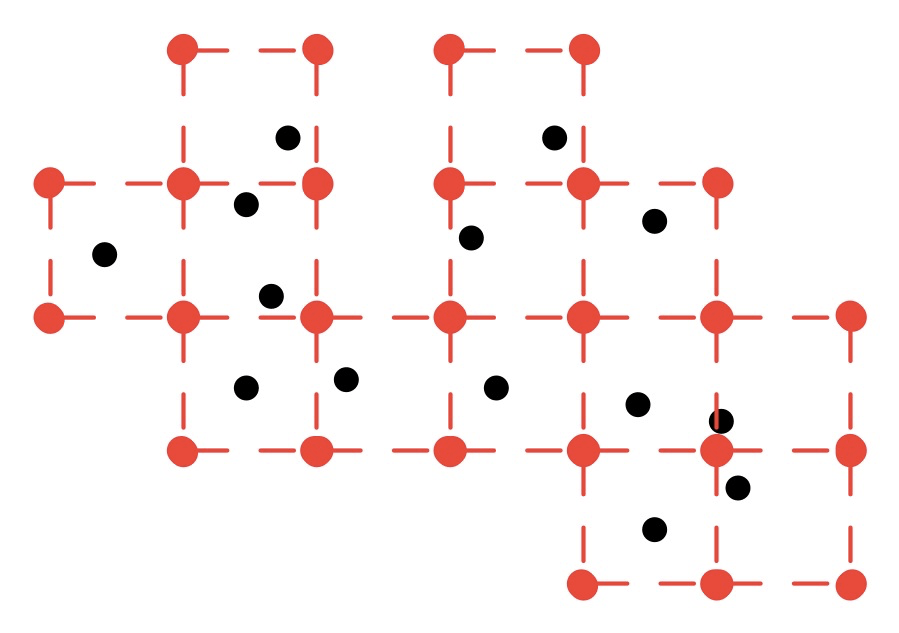
и для интервала сетки X/2, одним из возможных возвращаемых значений алгоритма будут координаты этих красных точек (пунктирные линии только для иллюстрации):

Для всех, кто интересуется, точки разупорядоченности, с которыми я работаю, - это атомные координаты больших белковых молекул, например, то, что вы можете получить из файла.pdb.

Python предпочтителен для решений, хотя псевдокод также хорош.

РЕДАКТИРОВАТЬ: я думаю, что мое первое описание того, что мне было нужно, может быть, немного нечетко, поэтому я добавил некоторые ограничения и изображения, чтобы прояснить вещи.

Answer 1

Поскольку вы запрашиваете регулярную квадратную сетку с указанным пользователем интервалом, похоже, что достаточно простой подход должен сработать.

Начните с передачи данных, чтобы определить минимальную и максимальную координаты в каждом измерении. Определите количество шагов заданного пользователем расстояния, необходимое для покрытия расстояния между максимумом и минимумом.

Повторно пропустите данные, чтобы выделить каждую точку ячейке в сетке, используя сетку с точкой как минимум каждой координаты и указанным интервалом (например, X_cell = Math.floor((x_i - x_min) / spacing)). Используйте словарь или массив для записи количества точек в каждой ячейке.

Теперь распечатайте координаты ячеек с хотя бы одной точкой в ​​них.

У вас есть некоторая свобода, которую я не пытался оптимизировать: если расстояние между минимальной и максимальной координатой не является точным кратным расстояния между сетками, будет некоторый наклон, который позволит вам перемещать сетку и при этом содержать ее. все точки: в данный момент сетка начинается в позиции самой низкой точки, но, вероятно, она заканчивается до самых высоких точек, поэтому у вас есть место, чтобы немного сдвинуть ее в каждом измерении. При этом некоторые точки будут перемещаться из ячейки в ячейку, и количество занятых ячеек будет меняться.

Если вы рассматриваете только движения в одном измерении за раз, вы можете решить, что произойдет достаточно эффективно. Определите расстояние в этом измерении между каждой точкой и максимальной координатой в этом измерении ее ячейки, а затем отсортируйте эти значения. При перемещении сетки вниз точка с наименьшим расстоянием до ее максимальной координаты сначала поменяет ячейки, и вы можете перемещаться по этим точкам одна за другой, перемещаясь по ним в отсортированном порядке. Если вы обновите количество точек в ячейках при этом, вы сможете определить, какой сдвиг минимизирует количество занятых ячеек.

Конечно, вам нужно беспокоиться о трех измерениях. Вы можете работать с ними по одному, пока не получите сокращение числа ячеек. Это локальный минимум, но не может быть глобальным минимумом. Один из способов поиска других локальных минимумов - начать заново со случайно выбранной начальной точки.

Answer 2

Я бы посоветовал вам сделать дерево кд. Это быстрый, простой и легкий в реализации:

И код Википедии:

class Node: pass

def kdtree(point_list, depth=0):
    if not point_list:
        return

    # Select axis based on depth so that axis cycles through all valid values
    k = len(point_list[0]) # assumes all points have the same dimension
    axis = depth % k

    # Sort point list and choose median as pivot element
    point_list.sort(key=lambda point: point[axis])
    median = len(point_list) // 2 # choose median

    # Create node and construct subtrees
    node = Node()
    node.location = point_list[median]
    node.left_child = kdtree(point_list[:median], depth + 1)
    node.right_child = kdtree(point_list[median + 1:], depth + 1)
    return node

Вы должны были бы немного изменить это, чтобы соответствовать вашим ограничениям.

Answer 3

Как насчет диаграммы Вороного? Это может быть сгенерировано в O(n log n) используя алгоритм Fortunes.

Я не знаю, решает ли это вашу проблему, но диаграммы Вороного очень "естественны". Они очень распространены в природе.

Пример (из Википедии):

Answer 4

Найдите квадрат минимальной площади, который охватывает все точки. Неоднократно подразделить каждый квадрат на 4 субквадрата (таким образом, переходя от 1 до 4 до 16 до 64 до...). Остановитесь прямо перед тем, как один из квадратов станет пустым. Нетрудно доказать, что результирующая сетка является не более чем в четыре раза более грубой, чем оптимальное решение (ключевая идея: гарантируется, что пустой квадрат содержит хотя бы один квадрат из любой сетки, по крайней мере, в два раза лучше).

Вероятно, эту константу можно уменьшить, введя случайный перевод.

Answer 5

У меня есть опыт работы с кластеризацией сетки в 2D и я реализовал пример в коде C#. http://kunuk.wordpress.com/2011/09/15/clustering-grid-cluster/

Это может обрабатывать пошаговые дескрипторы шагов 1, 2 и 4. Вам придется изменить код и обновить его до 3D-пространства. Надеюсь, что это дает вам некоторые идеи.

Код выполняется в O(m*n), где m - количество сеток, а n - количество точек.

Answer 6

Если вы хотите, чтобы ячейки сетки были квадратными и правильными, вам, скорее всего, нужен Octree. Если вы можете ослабить квадрат и регулярное ограничение, вы можете создать kd-дерево.