Найти количество вхождений подпоследовательности в строке
Например, пусть строка будет первые 10 цифр числа Пи, 3141592653и подпоследовательность будет 123, Обратите внимание, что последовательность происходит дважды:
3141592653
1 2 3
1 2 3
Это был вопрос интервью, на который я не мог ответить, и я не могу придумать эффективный алгоритм, и это меня беспокоит. Я чувствую, что это можно сделать с помощью простого регулярного выражения, но такие, как 1.*2.*3 не возвращайте каждую подпоследовательность. Моя наивная реализация в Python (считайте 3 для каждых 2 после каждого 1) работала в течение часа, и это не сделано.
8 ответов
Это классическая проблема динамического программирования (обычно не решаемая с помощью регулярных выражений).
Моя наивная реализация (считая 3 для каждых 2 после каждого 1) работала в течение часа, и это не сделано.
Это будет исчерпывающий подход к поиску, который выполняется в экспоненциальном времени. (Я удивлен, что работает несколько часов).
Вот предложение для решения динамического программирования:
План рекурсивного решения:
(Извиняюсь за длинное описание, но каждый шаг действительно прост, так что терпите меня;-)
Если подпоследовательность пуста, найдено совпадение (цифр не осталось!), И мы возвращаем 1
Если входная последовательность пуста, мы исчерпали наши цифры и не можем найти совпадение, поэтому мы возвращаем 0
(Ни последовательность, ни подпоследовательность не пусты.)
(Предположим, что " abcdef " обозначает входную последовательность, а " xyz " обозначает подпоследовательность.)
Задавать
resultдо 0Добавить к
resultколичество совпадений для bcdef и xyz (то есть, отбросить первую входную цифру и повторить)Если первые две цифры совпадают, то есть a = x
- Добавить к
resultколичество совпадений для bcdef и yz (т. е. совпадение с первой цифрой подпоследовательности и повторение по оставшимся цифрам подпоследовательности)
- Добавить к
Вернуть
result
пример
Вот иллюстрация рекурсивных вызовов для ввода 1221/12. (Подпоследовательность выделена жирным шрифтом, · представляет пустую строку.)
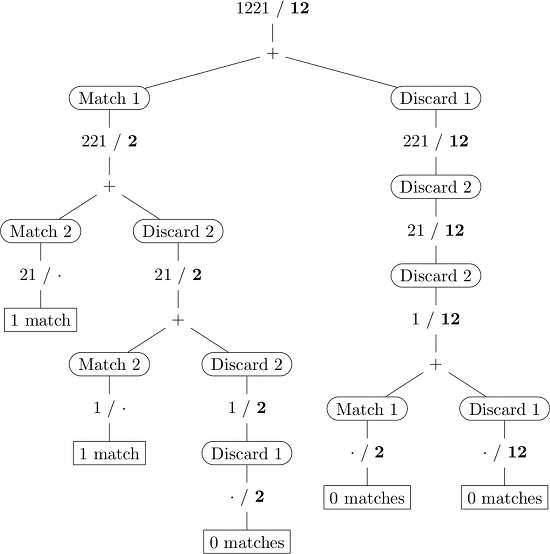
Динамическое программирование
Если реализовано наивно, некоторые (под) проблемы решаются многократно (например, · / 2 на иллюстрации выше). Динамическое программирование позволяет избежать таких избыточных вычислений, запоминая результаты ранее решенных подзадач (обычно в справочной таблице).
В этом конкретном случае мы создали таблицу с
- [длина последовательности + 1] строк и
- [длина подпоследовательности + 1] столбцов:

Идея состоит в том, что мы должны заполнить количество совпадений для 221/2 в соответствующей строке / столбце. После этого у нас должно быть окончательное решение в ячейке 1221/12.
Мы начинаем заполнять таблицу с того, что мы знаем немедленно ("базовые случаи"):
- Когда не осталось цифр подпоследовательности, мы имеем 1 полное совпадение:

Когда не осталось цифр последовательности, мы не можем найти совпадений:

Затем мы продолжаем, заполняя таблицу сверху вниз / слева направо согласно следующему правилу:
В ячейке [ row ] [ col ] напишите значение, найденное в [ row -1] [col].
Интуитивно это означает: "Количество совпадений за 221/2 включает все совпадения за 21/2".
Если последовательность в строке строки и подпоследовательность в столбце col начинаются с одной и той же цифры, добавьте значение, найденное в [ row -1] [ col -1], к только что записанному значению [ row ] [ col ].
Интуитивно это означает: "Количество совпадений за 1221/12 также включает все совпадения за 221/12".
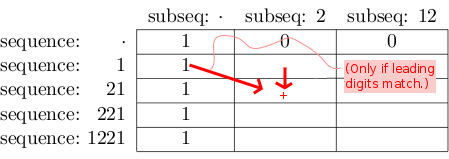
Окончательный результат выглядит следующим образом:
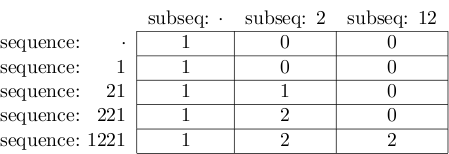
и значение в нижней правой ячейке действительно 2.
В коде
Не в Python, (мои извинения).
class SubseqCounter {
String seq, subseq;
int[][] tbl;
public SubseqCounter(String seq, String subseq) {
this.seq = seq;
this.subseq = subseq;
}
public int countMatches() {
tbl = new int[seq.length() + 1][subseq.length() + 1];
for (int row = 0; row < tbl.length; row++)
for (int col = 0; col < tbl[row].length; col++)
tbl[row][col] = countMatchesFor(row, col);
return tbl[seq.length()][subseq.length()];
}
private int countMatchesFor(int seqDigitsLeft, int subseqDigitsLeft) {
if (subseqDigitsLeft == 0)
return 1;
if (seqDigitsLeft == 0)
return 0;
char currSeqDigit = seq.charAt(seq.length()-seqDigitsLeft);
char currSubseqDigit = subseq.charAt(subseq.length()-subseqDigitsLeft);
int result = 0;
if (currSeqDigit == currSubseqDigit)
result += tbl[seqDigitsLeft - 1][subseqDigitsLeft - 1];
result += tbl[seqDigitsLeft - 1][subseqDigitsLeft];
return result;
}
}
сложность
Бонус за этот подход "заполнить стол" заключается в том, что вычислить сложность довольно просто. Постоянный объем работы выполняется для каждой ячейки, и у нас есть строки длины последовательности и столбцы длины последовательности. Сложность для этого O(MN), где M и N обозначают длины последовательностей.
Отличный ответ, aioobe! В дополнение к вашему ответу, некоторые возможные реализации в Python:
# straightforward, naïve solution; too slow!
def num_subsequences(seq, sub):
if not sub:
return 1
elif not seq:
return 0
result = num_subsequences(seq[1:], sub)
if seq[0] == sub[0]:
result += num_subsequences(seq[1:], sub[1:])
return result
# top-down solution using explicit memoization
def num_subsequences(seq, sub):
m, n, cache = len(seq), len(sub), {}
def count(i, j):
if j == n:
return 1
elif i == m:
return 0
k = (i, j)
if k not in cache:
cache[k] = count(i+1, j) + (count(i+1, j+1) if seq[i] == sub[j] else 0)
return cache[k]
return count(0, 0)
# top-down solution using the lru_cache decorator
# available from functools in python >= 3.2
from functools import lru_cache
def num_subsequences(seq, sub):
m, n = len(seq), len(sub)
@lru_cache(maxsize=None)
def count(i, j):
if j == n:
return 1
elif i == m:
return 0
return count(i+1, j) + (count(i+1, j+1) if seq[i] == sub[j] else 0)
return count(0, 0)
# bottom-up, dynamic programming solution using a lookup table
def num_subsequences(seq, sub):
m, n = len(seq)+1, len(sub)+1
table = [[0]*n for i in xrange(m)]
def count(iseq, isub):
if not isub:
return 1
elif not iseq:
return 0
return (table[iseq-1][isub] +
(table[iseq-1][isub-1] if seq[m-iseq-1] == sub[n-isub-1] else 0))
for row in xrange(m):
for col in xrange(n):
table[row][col] = count(row, col)
return table[m-1][n-1]
# bottom-up, dynamic programming solution using a single array
def num_subsequences(seq, sub):
m, n = len(seq), len(sub)
table = [0] * n
for i in xrange(m):
previous = 1
for j in xrange(n):
current = table[j]
if seq[i] == sub[j]:
table[j] += previous
previous = current
return table[n-1] if n else 1
Один из способов сделать это - два списка. Позвони им Ones а также OneTwos,
Пройдите строку, символ за символом.
- Всякий раз, когда вы видите цифру
1, сделайте запись вOnesсписок. - Всякий раз, когда вы видите цифру
2, пройти черезOnesсписок и добавить запись вOneTwosсписок. - Всякий раз, когда вы видите цифру
3, пройти черезOneTwosперечислить и вывести123,
В общем случае этот алгоритм будет очень быстрым, так как это один проход через строку и несколько проходов через то, что обычно будет намного меньшими списками. Патологические случаи убьют это, все же. Представьте себе строку как 111111222222333333, но с каждой цифрой повторяется сотни раз.
from functools import lru_cache
def subseqsearch(string,substr):
substrset=set(substr)
#fixs has only element in substr
fixs = [i for i in string if i in substrset]
@lru_cache(maxsize=None) #memoisation decorator applyed to recs()
def recs(fi=0,si=0):
if si >= len(substr):
return 1
r=0
for i in range(fi,len(fixs)):
if substr[si] == fixs[i]:
r+=recs(i+1,si+1)
return r
return recs()
#test
from functools import reduce
def flat(i) : return reduce(lambda x,y:x+y,i,[])
N=5
string = flat([[i for j in range(10) ] for i in range(N)])
substr = flat([[i for j in range(5) ] for i in range(N)])
print("string:","".join(str(i) for i in string),"substr:","".join(str(i) for i in substr),sep="\n")
print("result:",subseqsearch(string,substr))
вывод (мгновенно):
string:
00000000001111111111222222222233333333334444444444
substr:
0000011111222223333344444
result: 1016255020032
У меня есть интересное решение O(N) времени и пространства O(M) для этой задачи.
N - длина текста, а M - длина шаблона, который нужно найти. Я объясню вам алгоритм, потому что я реализую в C++.
Давайте предположим, что введенный вами ввод - 3141592653, а последовательность паттернов, число которых нужно найти, - 123 . Я начну с хеш-карты, которая отображает символы на их позиции в шаблоне ввода. Я также беру массив размера M, изначально инициализированный в 0.
string txt,pat;
cin >> txt >> pat;
int n = txt.size(),m = pat.size();
int arr[m];
map<char,int> mp;
map<char,int> ::iterator it;
f(i,0,m)
{
mp[pat[i]] = i;
arr[i] = 0;
}
Я начинаю искать элементы сзади и проверяю, есть ли каждый элемент в шаблоне или нет. Если этот элемент находится в шаблоне. Я должен чем-то заняться.
Теперь, когда я начинаю смотреть со спины, если я нахожу 2 и предыдущие, я не нашел никаких 3. Это 2 не имеет значения для нас. Потому что любой 1, найденный после того, как он сформирует такую последовательность 12 и 123, не будет сформирован Ryt? считать. Также в текущем положении я нашел 2, и он будет формировать последовательности 123 только с 3, найденными ранее, и сформирует x последовательностей, если мы нашли x 3 ранее (если будет найдена часть последовательности до 2). Таким образом, полный алгоритм заключается в том, что всякий раз, когда я нахожу элемент, который присутствует в массиве, я проверяю его позицию j, соответственно, в которой он присутствовал в шаблоне (хранится в хэш-карте). Я просто инкремент
arr[j] += arr[j+1];
означает, что это будет способствовать последовательности из 3, найденных до того, как это сделать? и если j найден m-1, я просто увеличу его
arr[j] += 1;
Проверьте фрагменты кода ниже, которые делают эти
for(int i = (n-1);i > -1;i--)
{
char ch = txt[i];
if(mp.find(ch) != mp.end())
{
int j = mp[ch];
if(j == (m-1))
arr[j]++;
else if(j < (m-1))
arr[j] += arr[j+1];
else
{;}
}
}
Теперь рассмотрим факт
каждый индекс i в массиве хранит количество раз, которое подстрока шаблона S[i,(m-1)] применяется как последовательность входной строки. Итак, в конце выведите значение arr[0]
cout << arr[0] << endl;
Код с выводом (уникальные символы в шаблоне) http://ideone.com/UWaJQF
Код с выводом (допускается повторение символов) http://ideone.com/14DZh7
Расширение работает только в том случае, если в шаблоне есть уникальные элементы. Что если в шаблоне есть уникальные элементы, то сложность может переместиться в O(MN). Решение аналогично без использования DP, только когда появился элемент, встречающийся в шаблоне, мы просто увеличили соответствующую ему позицию массива j, теперь мы имеем обновить все вхождения этих персонажей в паттерне, что приведет к сложности O(N* максимальная частота персонажа)
#define f(i,x,y) for(long long i = (x);i < (y);++i)
int main()
{
long long T;
cin >> T;
while(T--)
{
string txt,pat;
cin >> txt >> pat;
long long n = txt.size(),m = pat.size();
long long arr[m];
map<char,vector<long long> > mp;
map<char,vector<long long> > ::iterator it;
f(i,0,m)
{
mp[pat[i]].push_back(i);
arr[i] = 0;
}
for(long long i = (n-1);i > -1;i--)
{
char ch = txt[i];
if(mp.find(ch) != mp.end())
{
f(k,0,mp[ch].size())
{
long long j = mp[ch][k];
if(j == (m-1))
arr[j]++;
else if(j < (m-1))
arr[j] += arr[j+1];
else
{;}
}
}
}
cout <<arr[0] << endl;
}
}
может быть расширен аналогичным образом без DP в строках с повторениями, но тогда сложность будет больше O(MN)
Моя быстрая попытка:
def count_subseqs(string, subseq):
string = [c for c in string if c in subseq]
count = i = 0
for c in string:
if c == subseq[0]:
pos = 1
for c2 in string[i+1:]:
if c2 == subseq[pos]:
pos += 1
if pos == len(subseq):
count += 1
break
i += 1
return count
print count_subseqs(string='3141592653', subseq='123')
Изменить: этот должен быть правильным, если 1223 == 2 и более сложные случаи:
def count_subseqs(string, subseq):
string = [c for c in string if c in subseq]
i = 0
seqs = []
for c in string:
if c == subseq[0]:
pos = 1
seq = [1]
for c2 in string[i + 1:]:
if pos > len(subseq):
break
if pos < len(subseq) and c2 == subseq[pos]:
try:
seq[pos] += 1
except IndexError:
seq.append(1)
pos += 1
elif pos > 1 and c2 == subseq[pos - 1]:
seq[pos - 1] += 1
if len(seq) == len(subseq):
seqs.append(seq)
i += 1
return sum(reduce(lambda x, y: x * y, seq) for seq in seqs)
assert count_subseqs(string='12', subseq='123') == 0
assert count_subseqs(string='1002', subseq='123') == 0
assert count_subseqs(string='0123', subseq='123') == 1
assert count_subseqs(string='0123', subseq='1230') == 0
assert count_subseqs(string='1223', subseq='123') == 2
assert count_subseqs(string='12223', subseq='123') == 3
assert count_subseqs(string='121323', subseq='123') == 3
assert count_subseqs(string='12233', subseq='123') == 4
assert count_subseqs(string='0123134', subseq='1234') == 2
assert count_subseqs(string='1221323', subseq='123') == 5
Ответ Javascript, основанный на динамическом программировании от geeksforgeeks.org и ответ от aioobe:
class SubseqCounter {
constructor(subseq, seq) {
this.seq = seq;
this.subseq = subseq;
this.tbl = Array(subseq.length + 1).fill().map(a => Array(seq.length + 1));
for (var i = 1; i <= subseq.length; i++)
this.tbl[i][0] = 0;
for (var j = 0; j <= seq.length; j++)
this.tbl[0][j] = 1;
}
countMatches() {
for (var row = 1; row < this.tbl.length; row++)
for (var col = 1; col < this.tbl[row].length; col++)
this.tbl[row][col] = this.countMatchesFor(row, col);
return this.tbl[this.subseq.length][this.seq.length];
}
countMatchesFor(subseqDigitsLeft, seqDigitsLeft) {
if (this.subseq.charAt(subseqDigitsLeft - 1) != this.seq.charAt(seqDigitsLeft - 1))
return this.tbl[subseqDigitsLeft][seqDigitsLeft - 1];
else
return this.tbl[subseqDigitsLeft][seqDigitsLeft - 1] + this.tbl[subseqDigitsLeft - 1][seqDigitsLeft - 1];
}
}
Рзп. O(n) решения намного лучше.
Подумайте об этом, построив дерево:
Выполните итерацию по строке, если символ "1", добавьте узел в корень дерева. если символ "2", добавьте дочерний элемент к каждому узлу первого уровня. если символ "3", добавьте дочерний элемент к каждому узлу второго уровня.
вернуть количество узлов третьего уровня.
это было бы неэффективно, так что почему бы нам не сохранить количество узлов на каждую глубину:
infile >> in;
long results[3] = {0};
for(int i = 0; i < in.length(); ++i) {
switch(in[i]) {
case '1':
results[0]++;
break;
case '2':
results[1]+=results[0];
break;
case '3':
results[2]+=results[1];
break;
default:;
}
}
cout << results[2] << endl;
Как посчитать все трехчленные последовательности 1..2..3 в массиве цифр.
Быстро и просто
Обратите внимание, нам не нужно НАЙТИ все последовательности, нам нужно только СЧИТАТЬ их. Итак, все алгоритмы, которые ищут последовательности, являются чрезмерно сложными.
- Скинь каждую цифру, то есть не 1,2,3. Результатом будет массив символов A
- Сделайте параллельный массив int из 0. Запуск А с конца, подсчитайте для каждого 2 в А количество 3 в А после них. Поместите эти числа в соответствующие элементы B.
- Сделайте параллельный массив массива C из 0. Обработка A от конца подсчитывает для каждого 1 в A сумму B после его позиции. Результат положить в соответствующее место в C.
- Посчитайте сумму C.
Это все. Сложность O(N). Действительно, для обычной строки цифр это займет примерно вдвое больше времени сокращения строки источника.
Если последовательность будет более длинной, скажем, из M членов, процедура может быть повторена M раз. И сложность будет O(MN), где N уже будет длина сокращенной строки источника.