Не максимальное подавление

Мы узнали, что вы можете получить направление градиента с atan(dy/dx) который является направлением, ортогональным к краю. Теперь у нас было домашнее задание, в котором мы должны были разделить это направление на четыре класса (x- и y-направление и обе диагонали), а затем проверить соседей пикселей в лучшем подходящем направлении для подавления не макс.

Я не полностью получил решение, хотя. Очевидно, у нас было четыре случая:

  1. abs(angle) < pi/8Таким образом, градиент (примерно) указывает в направлении х, поэтому мы проверяем img(i, j-1) а также img(i, j+1) (при условии, что источник изображения находится вверху слева)

  2. angle > pi/8 && angle <= 3*pi/8таким образом, градиент указывает на верхний правый угол. Теперь я думал, что мы должны проверить img(i-1, j+1) а также img(i+1, j-1) но вместо этого мы проверяем img(i-1, j-1) а также img(i+1, j+1) которая выглядит как ортогональная диагональ.

Два других случая эквивалентны. Я пытался изменить это, но тогда края действительно выглядят странно, так что это кажется правильным, но я не понимаю почему.

Может кто-то объяснить это мне?

Источник

3 ответа

Решение

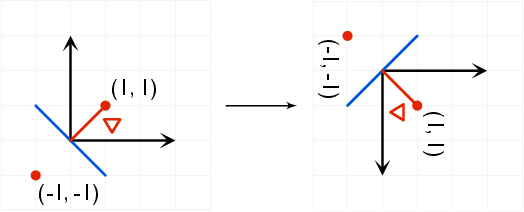
Немаксиальное подавление - это способ устранения точек, которые не лежат на важных ребрах. В вашем первом случае, если градиент близок к нулю градусов в данной точке, это означает, что край находится на севере или на юге, и эта точка будет считаться краем, если величина этой точки больше обе величины точек слева и справа (как в вашем примере). Во втором случае вы проверяете градиент под углом 45 градусов, то есть край равен 135 градусам, и вы сохраняете точку, если она больше точек вдоль направления градиента, то есть (-1, -1) и (1 1). Вращение системы координат не влияет на это.

Источник

Вот реализация Python для функции " Не подавление максимума", используемой в процессе обнаружения Canny Edge.

Они сосредоточены на севере и юге, северо-востоке и юго-западе, востоке и западе, а также на юго-востоке и северо-западе. Затем решите, какие значения сохранить.

Надеюсь, это поможет кому-то, кому нужна NMS, чтобы найти лучшее преимущество.

Источник

Может быть, опоздал на исходный вопрос, но следующая ссылка может помочь любому, кто пытается понять не-максимальное подавление.

Java Демо не макс подавления

Источник
Другие вопросы по тегам