Генерация случайных чисел с заданным (числовым) распределением
У меня есть файл с некоторыми вероятностями для разных значений, например:
1 0.1
2 0.05
3 0.05
4 0.2
5 0.4
6 0.2
Я хотел бы генерировать случайные числа с помощью этого распределения. Существует ли существующий модуль, который обрабатывает это? Довольно просто написать код самостоятельно (построить функцию кумулятивной плотности, сгенерировать случайное значение [0,1] и выбрать соответствующее значение), но кажется, что это должно быть распространенной проблемой, и, возможно, кто-то создал функцию / модуль для Это.
Мне это нужно, потому что я хочу сгенерировать список дней рождения (которые не соответствуют ни одному распределению в стандарте random модуль).
12 ответов
scipy.stats.rv_discrete может быть, что вы хотите. Вы можете указать свои вероятности через values параметр. Затем вы можете использовать rvs() метод распределения объекта для генерации случайных чисел.
Как отметил Евгений Пахомов в комментариях, вы также можете передать p параметр ключевого слова для numpy.random.choice() например,
numpy.random.choice(numpy.arange(1, 7), p=[0.1, 0.05, 0.05, 0.2, 0.4, 0.2])
Если вы используете Python 3.6 или выше, вы можете использовать random.choices() из стандартной библиотеки - см. ответ Марка Дикинсона.
Начиная с Python 3.6, есть решение для этого в стандартной библиотеке Python, а именно random.choices,
Пример использования: давайте настроим совокупность и веса, соответствующие тем, которые указаны в вопросе ОП:
>>> from random import choices
>>> population = [1, 2, 3, 4, 5, 6]
>>> weights = [0.1, 0.05, 0.05, 0.2, 0.4, 0.2]
Сейчас choices(population, weights) генерирует один образец:
>>> choices(population, weights)
4
Необязательный аргумент только для ключевых слов k позволяет запрашивать более одного образца одновременно. Это ценно, потому что есть некоторые подготовительные работы, которые random.choices должен делать каждый раз, когда он вызывается, до генерации каких-либо сэмплов; генерируя много образцов одновременно, нам нужно выполнить эту подготовительную работу только один раз. Здесь мы генерируем миллион образцов и используем collections.Counter чтобы проверить, что распределение, которое мы получаем, примерно соответствует весам, которые мы дали.
>>> million_samples = choices(population, weights, k=10**6)
>>> from collections import Counter
>>> Counter(million_samples)
Counter({5: 399616, 6: 200387, 4: 200117, 1: 99636, 3: 50219, 2: 50025})
Преимущество создания списка с использованием CDF заключается в том, что вы можете использовать бинарный поиск. В то время как вам нужно O (n) время и пространство для предварительной обработки, вы можете получить k чисел в O(k log n). Так как обычные списки Python неэффективны, вы можете использовать array модуль.
Если вы настаиваете на постоянном месте, вы можете сделать следующее; O(n) время, O(1) пространство.
def random_distr(l):
r = random.uniform(0, 1)
s = 0
for item, prob in l:
s += prob
if s >= r:
return item
return item # Might occur because of floating point inaccuracies
(Хорошо, я знаю, что вы спрашиваете об упаковке в термоусадочную пленку, но, возможно, эти домашние решения не были достаточно краткими для вашего вкуса.:-)
pdf = [(1, 0.1), (2, 0.05), (3, 0.05), (4, 0.2), (5, 0.4), (6, 0.2)]
cdf = [(i, sum(p for j,p in pdf if j < i)) for i,_ in pdf]
R = max(i for r in [random.random()] for i,c in cdf if c <= r)
Я псевдо-подтвердил, что это работает, глядя на результат этого выражения:
sorted(max(i for r in [random.random()] for i,c in cdf if c <= r)
for _ in range(1000))
Может быть, уже поздно. Но вы можете использовать numpy.random.choice() минуя p параметр:
val = numpy.random.choice(numpy.arange(1, 7), p=[0.1, 0.05, 0.05, 0.2, 0.4, 0.2])
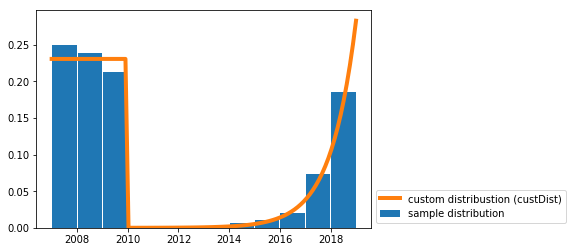
Я написал решение для рисования случайных выборок из пользовательского непрерывного распределения.
Мне это нужно для аналогичного случая использования (например, генерация случайных дат с заданным распределением вероятности).
Вам просто нужна функция random_custDist и линия samples=random_custDist(x0,x1,custDist=custDist,size=1000), Остальное украшение ^^.
import numpy as np
#funtion
def random_custDist(x0,x1,custDist,size=None, nControl=10**6):
#genearte a list of size random samples, obeying the distribution custDist
#suggests random samples between x0 and x1 and accepts the suggestion with probability custDist(x)
#custDist noes not need to be normalized. Add this condition to increase performance.
#Best performance for max_{x in [x0,x1]} custDist(x) = 1
samples=[]
nLoop=0
while len(samples)<size and nLoop<nControl:
x=np.random.uniform(low=x0,high=x1)
prop=custDist(x)
assert prop>=0 and prop<=1
if np.random.uniform(low=0,high=1) <=prop:
samples += [x]
nLoop+=1
return samples
#call
x0=2007
x1=2019
def custDist(x):
if x<2010:
return .3
else:
return (np.exp(x-2008)-1)/(np.exp(2019-2007)-1)
samples=random_custDist(x0,x1,custDist=custDist,size=1000)
print(samples)
#plot
import matplotlib.pyplot as plt
#hist
bins=np.linspace(x0,x1,int(x1-x0+1))
hist=np.histogram(samples, bins )[0]
hist=hist/np.sum(hist)
plt.bar( (bins[:-1]+bins[1:])/2, hist, width=.96, label='sample distribution')
#dist
grid=np.linspace(x0,x1,100)
discCustDist=np.array([custDist(x) for x in grid]) #distrete version
discCustDist*=1/(grid[1]-grid[0])/np.sum(discCustDist)
plt.plot(grid,discCustDist,label='custom distribustion (custDist)', color='C1', linewidth=4)
#decoration
plt.legend(loc=3,bbox_to_anchor=(1,0))
plt.show()
Производительность этого решения наверняка улучшена, но я предпочитаю удобочитаемость.
Составьте список предметов, основываясь на их weights:
items = [1, 2, 3, 4, 5, 6]
probabilities= [0.1, 0.05, 0.05, 0.2, 0.4, 0.2]
# if the list of probs is normalized (sum(probs) == 1), omit this part
prob = sum(probabilities) # find sum of probs, to normalize them
c = (1.0)/prob # a multiplier to make a list of normalized probs
probabilities = map(lambda x: c*x, probabilities)
print probabilities
ml = max(probabilities, key=lambda x: len(str(x)) - str(x).find('.'))
ml = len(str(ml)) - str(ml).find('.') -1
amounts = [ int(x*(10**ml)) for x in probabilities]
itemsList = list()
for i in range(0, len(items)): # iterate through original items
itemsList += items[i:i+1]*amounts[i]
# choose from itemsList randomly
print itemsList
Оптимизация может состоять в том, чтобы нормализовать суммы по наибольшему общему делителю, чтобы уменьшить целевой список.
Также это может быть интересно.
from __future__ import division
import random
from collections import Counter
def num_gen(num_probs):
# calculate minimum probability to normalize
min_prob = min(prob for num, prob in num_probs)
lst = []
for num, prob in num_probs:
# keep appending num to lst, proportional to its probability in the distribution
for _ in range(int(prob/min_prob)):
lst.append(num)
# all elems in lst occur proportional to their distribution probablities
while True:
# pick a random index from lst
ind = random.randint(0, len(lst)-1)
yield lst[ind]
Проверка:
gen = num_gen([(1, 0.1),
(2, 0.05),
(3, 0.05),
(4, 0.2),
(5, 0.4),
(6, 0.2)])
lst = []
times = 10000
for _ in range(times):
lst.append(next(gen))
# Verify the created distribution:
for item, count in Counter(lst).iteritems():
print '%d has %f probability' % (item, count/times)
1 has 0.099737 probability
2 has 0.050022 probability
3 has 0.049996 probability
4 has 0.200154 probability
5 has 0.399791 probability
6 has 0.200300 probability
Еще один ответ, наверное, быстрее:)
distribution = [(1, 0.2), (2, 0.3), (3, 0.5)]
# init distribution
dlist = []
sumchance = 0
for value, chance in distribution:
sumchance += chance
dlist.append((value, sumchance))
assert sumchance == 1.0 # not good assert because of float equality
# get random value
r = random.random()
# for small distributions use lineair search
if len(distribution) < 64: # don't know exact speed limit
for value, sumchance in dlist:
if r < sumchance:
return value
else:
# else (not implemented) binary search algorithm
Возможно, вы захотите взглянуть на распределение случайных выборок NumPy
Основываясь на других решениях, вы генерируете накопительное распределение (как целое число или число с плавающей запятой, что хотите), а затем можете использовать bisect, чтобы сделать это быстро
это простой пример (здесь я использовал целые числа)
l=[(20, 'foo'), (60, 'banana'), (10, 'monkey'), (10, 'monkey2')]
def get_cdf(l):
ret=[]
c=0
for i in l: c+=i[0]; ret.append((c, i[1]))
return ret
def get_random_item(cdf):
return cdf[bisect.bisect_left(cdf, (random.randint(0, cdf[-1][0]),))][1]
cdf=get_cdf(l)
for i in range(100): print get_random_item(cdf),
get_cdf функция будет преобразовывать его из 20, 60, 10, 10 в 20, 20 + 60, 20 + 60 + 10, 20 + 60 + 10 + 10
Теперь мы выбираем случайное число до 20 + 60 + 10 + 10, используя random.randint Затем мы используем bisect, чтобы быстро получить фактическое значение
Ни один из этих ответов не является особенно ясным или простым.
Вот ясный, простой метод, который гарантированно работает.
аккумулировать_нормализировать_процедуры принимает словарь p который отображает символы на вероятности или частоты. Он выводит пригодный для использования список кортежей, из которых можно сделать выбор.
def accumulate_normalize_values(p):
pi = p.items() if isinstance(p,dict) else p
accum_pi = []
accum = 0
for i in pi:
accum_pi.append((i[0],i[1]+accum))
accum += i[1]
if accum == 0:
raise Exception( "You are about to explode the universe. Continue ? Y/N " )
normed_a = []
for a in accum_pi:
normed_a.append((a[0],a[1]*1.0/accum))
return normed_a
Урожайность:
>>> accumulate_normalize_values( { 'a': 100, 'b' : 300, 'c' : 400, 'd' : 200 } )
[('a', 0.1), ('c', 0.5), ('b', 0.8), ('d', 1.0)]
Почему это работает
Этап накопления превращает каждый символ в интервал между собой и вероятностью или частотой предыдущих символов (или 0 в случае первого символа). Эти интервалы можно использовать для выбора (и, следовательно, выборки из предоставленного распределения), просто перемещаясь по списку, пока случайное число в интервале 0.0 -> 1.0 (подготовленное ранее) не станет меньше или равно конечной точке текущего интервала символа.
Нормализация освобождает нас от необходимости удостовериться, что все соответствует некоторой ценности. После нормализации "вектор" вероятностей суммируется в 1,0.
Остальная часть кода для выбора и генерации произвольно длинной выборки из дистрибутива приведена ниже:
def select(symbol_intervals,random):
print symbol_intervals,random
i = 0
while random > symbol_intervals[i][1]:
i += 1
if i >= len(symbol_intervals):
raise Exception( "What did you DO to that poor list?" )
return symbol_intervals[i][0]
def gen_random(alphabet,length,probabilities=None):
from random import random
from itertools import repeat
if probabilities is None:
probabilities = dict(zip(alphabet,repeat(1.0)))
elif len(probabilities) > 0 and isinstance(probabilities[0],(int,long,float)):
probabilities = dict(zip(alphabet,probabilities)) #ordered
usable_probabilities = accumulate_normalize_values(probabilities)
gen = []
while len(gen) < length:
gen.append(select(usable_probabilities,random()))
return gen
Использование:
>>> gen_random (['a','b','c','d'],10,[100,300,400,200])
['d', 'b', 'b', 'a', 'c', 'c', 'b', 'c', 'c', 'c'] #<--- some of the time
Вот более эффективный способ сделать это:
Просто вызовите следующую функцию с вашим массивом weights (при условии, что индексы являются соответствующими элементами) и no. образцов необходимо. Эта функция может быть легко изменена для обработки упорядоченной пары.
Возвращает индексы (или элементы), отобранные / выбранные (с заменой) с использованием их соответствующих вероятностей:
def resample(weights, n):
beta = 0
# Caveat: Assign max weight to max*2 for best results
max_w = max(weights)*2
# Pick an item uniformly at random, to start with
current_item = random.randint(0,n-1)
result = []
for i in range(n):
beta += random.uniform(0,max_w)
while weights[current_item] < beta:
beta -= weights[current_item]
current_item = (current_item + 1) % n # cyclic
else:
result.append(current_item)
return result
Краткое примечание о концепции, используемой в цикле while. Мы уменьшаем вес текущего элемента из кумулятивной бета-версии, которая представляет собой совокупное значение, построенное равномерно случайным образом, и увеличиваем текущий индекс, чтобы найти элемент, вес которого соответствует значению бета-версии.