Нахождение скользящего среднего по точкам данных в Python
Я снова немного играю в Python, и я нашел аккуратную книгу с примерами. Одним из примеров является представление некоторых данных. У меня есть файл.txt с двумя столбцами, и у меня есть данные. Я нанес на карту данные очень хорошо, но в упражнении говорится: "Измените вашу программу дальше, чтобы вычислить и построить график скользящего среднего данных, определяемого как:
$Y_k=\frac{1}{2r}\sum_{m=-r}^r y_{k+m}$
где r=5 в этом случае (и y_k это второй столбец в файле данных). Пусть программа отобразит как исходные данные, так и скользящее среднее на одном графике.
Пока у меня есть это:
from pylab import plot, ylim, xlim, show, xlabel, ylabel
from numpy import linspace, loadtxt
data = loadtxt("sunspots.txt", float)
r=5.0
x = data[:,0]
y = data[:,1]
plot(x,y)
xlim(0,1000)
xlabel("Months since Jan 1749.")
ylabel("No. of Sun spots")
show()
Так как мне рассчитать сумму? В Mathematica это просто, поскольку это символическое манипулирование (например, Sum[i, {i,0,10}]), но как вычислить сумму в python, которая берет каждые десять точек в данных и усредняет их, и делает это до конца очков?
Я посмотрел на книгу, но не нашел ничего, что могло бы объяснить это:
Хелтонбайкер код сделал свое дело ^^:D
from __future__ import division
from pylab import plot, ylim, xlim, show, xlabel, ylabel, grid
from numpy import linspace, loadtxt, ones, convolve
import numpy as numpy
data = loadtxt("sunspots.txt", float)
def movingaverage(interval, window_size):
window= numpy.ones(int(window_size))/float(window_size)
return numpy.convolve(interval, window, 'same')
x = data[:,0]
y = data[:,1]
plot(x,y,"k.")
y_av = movingaverage(y, 10)
plot(x, y_av,"r")
xlim(0,1000)
xlabel("Months since Jan 1749.")
ylabel("No. of Sun spots")
grid(True)
show()
И я получил это:
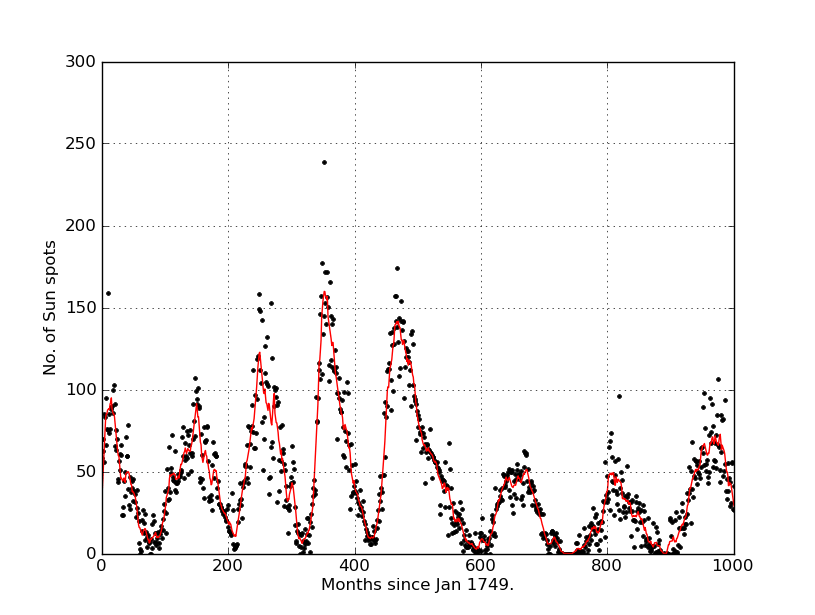
Большое спасибо ^^:)
7 ответов
Прежде чем читать этот ответ, имейте в виду, что ниже есть другой ответ от Романа Х, который использует
numpy.cumsumи НАМНОГО БОЛЬШЕ, чем этот.
Лучший из распространенных способов применения скользящего / скользящего среднего (или любой другой функции скользящего окна) к сигналу - использование numpy.convolve(),
def movingaverage(interval, window_size):
window = numpy.ones(int(window_size))/float(window_size)
return numpy.convolve(interval, window, 'same')
Здесь интервал ваш x массив и window_size количество образцов для рассмотрения. Окно будет центрировано по каждому сэмплу, поэтому он берет сэмплы до и после текущего сэмпла, чтобы вычислить среднее значение. Ваш код станет:
plot(x,y)
xlim(0,1000)
x_av = movingaverage(interval, r)
plot(x_av, y)
xlabel("Months since Jan 1749.")
ylabel("No. of Sun spots")
show()
Надеюсь это поможет!
Поскольку numpy.convolve довольно медленный, те, кто нуждается в быстродействующем решении, могут предпочесть более простой для понимания подход cumsum. Вот код:
cumsum_vec = numpy.cumsum(numpy.insert(data, 0, 0))
ma_vec = (cumsum_vec[window_width:] - cumsum_vec[:-window_width]) / window_width
где данные содержат ваши данные, а ma_vec будет содержать скользящие средние длины window_width.
В среднем, кончум примерно в 30-40 раз быстрее, чем свертка.
Скользящее среднее - это свертка, и numpy будет быстрее, чем большинство чистых операций с Python. Это даст вам 10-балльную скользящую среднюю.
import numpy as np
smoothed = np.convolve(data, np.ones(10)/10)
Я также настоятельно рекомендую использовать пакет великолепных панд, если вы работаете с данными временных рядов. Есть несколько хороших встроенных операций скользящего среднего.
ravgs = [sum(data[i:i+5])/5. for i in range(len(data)-4)]
Это не самый эффективный подход, но он даст ваш ответ, и мне неясно, будет ли ваше окно 5 баллов или 10. Если его 10, замените каждые 5 на 10, а 4 на 9.
Есть проблема с принятым ответом. Я думаю, что нам нужно использовать "действительный" вместо "тот же" здесь - return numpy.convolve(interval, window, 'same'),
В качестве примера попробуйте MA этого набора данных = [1,5,7,2,6,7,8,2,2,7,8,3,7,3,7,3,15,6] - результат должен быть [4.2,5.4,6.0,5.0,5.0,5.2,5.4,4.4,5.4,5.6,5.6,4.6,7.0,6.8], но "то же самое" дает нам неправильный вывод [2.6,3.0,4.2,5.4,6.0,5.0,5.0,5.2,5.4,4.4,5.4,5.6,5.6, 4.6,7.0,6.8,6.2,4.8]
Расти код, чтобы попробовать это -:
result=[]
dataset=[1,5,7,2,6,7,8,2,2,7,8,3,7,3,7,3,15,6]
window_size=5
for index in xrange(len(dataset)):
if index <=len(dataset)-window_size :
tmp=(dataset[index]+ dataset[index+1]+ dataset[index+2]+ dataset[index+3]+ dataset[index+4])/5.0
result.append(tmp)
else:
pass
result==movingaverage(y, window_size)
Попробуйте это с valid & same и посмотрите, имеет ли математика смысл.
Функция My Moving Average, без функции numpy:
from __future__ import division # must be on first line of script
class Solution:
def Moving_Avg(self,A):
m = A[0]
B = []
B.append(m)
for i in range(1,len(A)):
m = (m * i + A[i])/(i+1)
B.append(m)
return B
Я думаю что-то вроде:
aves = [sum(data[i:i+6]) for i in range(0, len(data), 5)]
Но я всегда должен дважды проверять, что индексы делают то, что я ожидаю. Требуемый диапазон (0, 5, 10, ...) и данные [0:6] предоставят вам данные [0]... данные [5]
ETA: упс, и вы хотите ave, а не sum, конечно. Итак, на самом деле, используя ваш код и формулу:
r = 5
x = data[:,0]
y1 = data[:,1]
y2 = [ave(y1[i-r:i+r]) for i in range(r, len(y1), 2*r)]
y = [y1, y2]