Реализация дерева диапазонов

Question

Я пытаюсь реализовать дерево диапазонов, но я действительно запутался, вот мой текст:

Теперь предположим, что у меня есть такое дерево:

И я хочу найти точки между 14 и 19. V_Split здесь было бы 17, и, переходя от 17 к 14, согласно алгоритму, я должен сообщить правильное поддерево 17, которое является 23 и 19. Но 23 не между 14 и 19. Что мне здесь делать?

Если я не рассматриваю 17, то о 17 не будет сообщено. И еще раз, если я хочу найти точки между 12 и 19, 14 не будут включены!

Answer 1

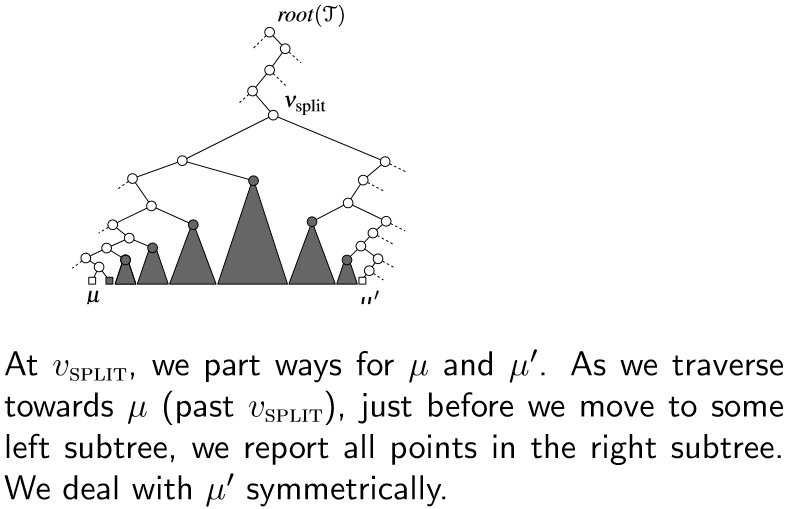
Некоторое время назад я реализовал шаги, описанные в статье " Дерево диапазонов" в Википедии (раздел "Запросы диапазона"), они похожи на ваш текст. Основная идея состоит в том, чтобы найти точку vsplit, а затем выполнить двоичный поиск левого и правого дочерних элементов vsplit, захватывая все узлы "в диапазоне" по мере движения.

Я хотел, чтобы структура данных (TreeNode) была действительно простой, чтобы ее было легче понять (поскольку я не видел необходимости хранить каждый узел в виде листьев, как предполагает статья?). Во всяком случае, ниже вы можете найти основной метод для моего класса, он содержит общую идею, объясненную шаг за шагом. Не стесняйтесь захватить весь код из моего репозитория github, но я бы посоветовал сначала попытаться самостоятельно написать код getLeftNodes () / getRightNodes ().

    /**
     * Range trees can be used to find the set of points that lay inside a given
     * interval. To report the points that lie in the interval [x1, x2], we
     * start by searching for x1 and x2.
     * 
     * The following method will use a regular balanced binary search tree for
     * this purpose. More info in https://en.wikipedia.org/wiki/Range_tree
     * 
     * @param x1
     *            Low (start) range position
     * @param x2
     *            High (end) range position
     * @param root
     *            A balanced binary search tree root
     * @return
     */
    public HashSet<Integer> getNodesInRange(int x1, int x2, TreeNode root) {
        if (x1 >= x2) {
            throw new IllegalArgumentException("Range error: x1 must be less than x2");
        }

        // At some vertex in the tree, the search paths to x1 and x2 will
        // diverge. Let vsplit be the last vertex that these two search paths
        // have in common.
        TreeNode vsplit = root;
        while (vsplit != null) {
            if (x1 < vsplit.data && x2 < vsplit.data) {
                vsplit = vsplit.left;
            } else if (x1 > vsplit.data && x2 > vsplit.data) {
                vsplit = vsplit.right;
            } else {
                break;
            }
        }

        // Report the value stored at vsplit if it is inside the query interval.
        HashSet<Integer> nodesInRange = new HashSet<>();
        if (vsplit == null) {
            return nodesInRange;
        } else if (inRange(vsplit.data, x1, x2)) {
            nodesInRange.add(vsplit.data);
        }

        // Continue searching for x1 in the range tree (vSplit to x1).
        getLeftNodes(x1, x2, nodesInRange, vsplit.left);
        // Continue searching for x2 in the range tree (vSplit to x2).
        getRightNodes(x1, x2, nodesInRange, vsplit.right);

        return nodesInRange;
    }

Целевая временная сложность для этой реализации должна быть O (log (n)), так как мы выполняем три двоичных поиска (vsplit + left + right), принимая O (log (n)) для каждого из них, поэтому он также должен быть прилично эффективным.

Кодирование помогло мне понять общую идею дерева диапазонов (очень полезно в задачах кода), и я надеюсь, что он сделает то же самое для вас.

Примечание: я уверен, что есть еще более простые реализации (и более эффективные)!